Francesco Casella

@AnHeuermann the residuals are ok, so once you get convergence, the result is of course fine. The problem is that _a wrong Jacobian hampers the convergence_. And since the relevant...

> My reasoning is, that the solution is correct, so the right hand side of the ODE should be correct Yes. > and then the numeric Jacobian has to be...

We made a debugging session today with @AnHeuermann. The way the numerical Jacobian is computed by the runtime is a bit odd-looking because it makes extensive use of a lot...

We just checked the simulation with `-jacobian=internalNumerical` and we got more or less equally bad performance both with DASSL and IDA, so the problem is not with the numerical differentiation,...

@AnHeuermann, here is some more analysis on the model to figure out what is going wrong > The non-zero elements of the first 6 rows of the numerical Jacobian are...

This is a plot of the step size versus step number 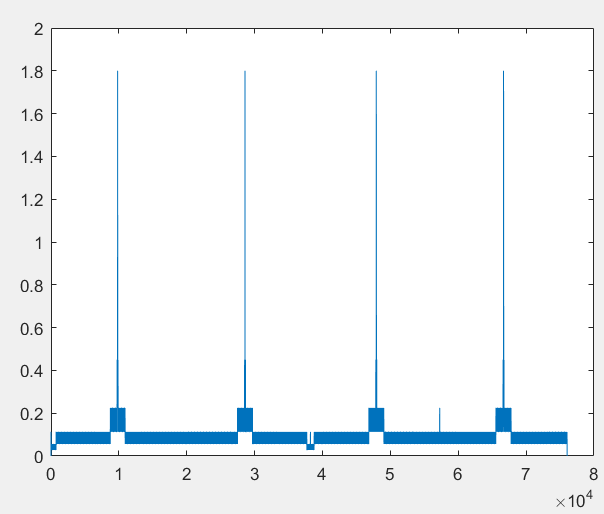 This is a plot of the step size versus simulation time 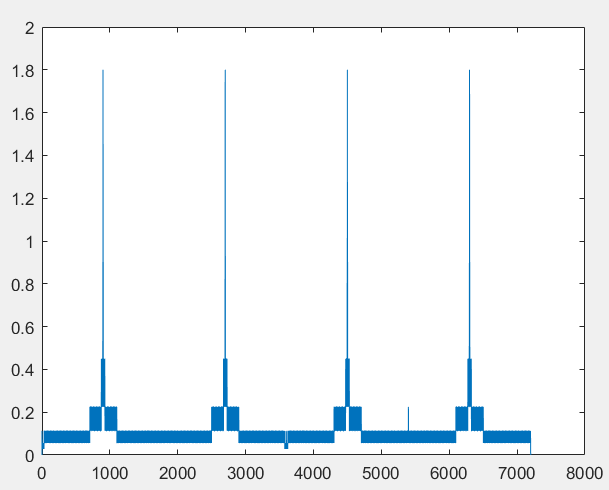 This is a plot of of...

The smoothing of the Heaviside function looks wide enough to be effective: 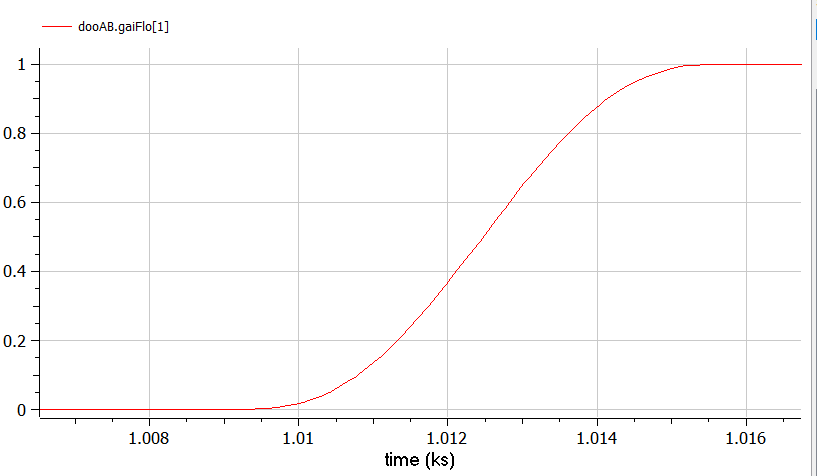 so it's not that the smoothHeaviside function is so sharp that it behaves like a normal Heaviside...

@AnHeuermann to summarize: the model to compute the flow rates is smooth (two times continuously differentiable), but apparently something's going wrong with the way the residuals involving them (the first...

I checked, the `smoothHeaviside` function is not inlined, this is the generated C-code: ```C modelica_real omc_Buildings_Utilities_Math_Functions_smoothHeaviside(threadData_t *threadData, modelica_real _x, modelica_real _delta) { modelica_real _y; modelica_real _dx; modelica_real tmp1; modelica_real _xpow2;...

OK. I would prioritize the parameter-dependent case over the discrete-variable dependent case, though probably you can handle them together, since the first is a special case of the second, which...