Introduction

This is a collection of adaptive control methods from the book "Adaptive Control" by Karl Johan Åström and Björn Wittenmark. They are the masters of the classical methods for self tuning controllers. The book is made for an industrial audience and PhD students in control theory. Those control methods is most used for hydraulic and electrical servo systems in space engineering and flight engineering and also in advanced control engineering problems for robotics at the industry.

The book has sevral interesting control methods:

* Linear Quadratic Regulator (LQR) - For optimal systems
* Linear Quadratic Gaussian (LQG) - With kalman filtering
* Linear Quadratic Estimator (LQE) - Finding the kalman gain matrix
* Generalized Predictive Controller (GPC) - For future prediction
* Self Tuning Regulator (STR) - For deterministic systems
* Minimum Variance Controller (MVC) - For heavy stochastical systems 
* Model Reference Adaptive Controller (MRAC) - For smooth reference tracking
* Extended Least Square (ELS) - For estimate stochastical models e.g ARMAX models
* Recursive Least Square (RLS) - For estimate transfer functions

The book does not contain this, but I have by my self read lots of papes about subspace identification and constrained control. At the bottom of this page, I will present:

* Adaptive Constrained MPC (ERAOKIDMPC) - Using Subspace identification methods

The collection is made by the open source software Scilab and Xcox 6.0.1 and the book "Adaptive Control"

C code

If you want to try adaptive control with C-code. Have a look at this. It also work for embedded systems. MATLAB-files and C-code files as examples is available:

https://github.com/DanielMartensson/CControl

Unscented Kalman Filter

I very good filter for you is the Unscented Kalman Filter for nonlinear and linear systems. Easy to use and easier than regular kalman filter.

https://github.com/DanielMartensson/Unscented-Kalman-Filter

Square Root Uncented Kalman Filter for state estimation and parameter estimation

A very good algorithm located in here.

https://github.com/DanielMartensson/MataveID

Identification library

If you want to identify models, then this library is for you - Mataveid.

https://github.com/DanielMartensson/mataveid

Linear Quadratic Regulator

Diagram of the LQR system Simulation of the LQR system. The green signal is the input signal and the black signal is the output signal. Between 0 to 50 seconds, the estimator learn the system behaviour. Parameter estimation of the LQR system.

Linear Quadratic Gaussian

Diagram of the LQG system. Here we can se that the system has a LQE - Linear Quadratic estimator and a Kalman Filter Simulation of the LQG system. Green is our input signal, black is our noisy output signal and red is our filtered output signal by using a kalman filter.

Generalized Predictive Control

Diagram of the GPC system Simulation of the GPC system. The green line is our reference following line and the black line is the system output. There is the input signal. Between 0 to 30 seconds, the GPC controller learns the system behaviour.

Self Tuning Regulator - Minimum phase system

Diagram of the STR system with minimum phase. Here I use Recursive Least Square and STR learning the system between 0 to 15 seconds, then tune the STR controller.

Self Tuning Regulator - Non-Minimum phase system

Diagram of the STR system with non-minimum phase. The difference between non-minimum phase and minimum phase is that non-minimum phase has zeros at the right half plane and minimum phase has zeros on the left half plane. On other words, non-minimum phase is much more difficult to handle.

Minimum Variance Controller

Diagram of the MVC system. I'm using Extended Least Square to estimate a ARMAX model, it's a transfer function with disturbance.

Simulation of the MVC system. Here is green the input signal and black the output signal. Between 0 to 70 seconds, the MVC self learning the disturbance.

Here is the parameter estimation for the ARMAX model.

Model Reference Adaptive Controller - MIT Rule

Diagram of MRAC system with uning of MIT rule

Simulation of MRAC system

Model Reference Adaptive Controller - Lyapunov Rule

Diagram of MRAC system with uning of Lyapunov rule

Simulation of MRAC system. According to me - Lyapunov is much better than MIT rule.

Extended Least Square

Diagram of ELS

Simulation of ELS. Here is the green signal our measured signal and the black signal is our estimated signal.

Parameter estimation

Recursive Least Square

Diagram of RLS

Simulation of RLS

Parameter estimation of RLS

Adaptive Constrained MPC

This simulation uses Eigensystem Realization Algorithm and Observer Kalmanfilter Identifcation to estimate a state space model by using the subspace identification technique. Minimal data is used. The code is available inside the Octave folder.

Second order system:

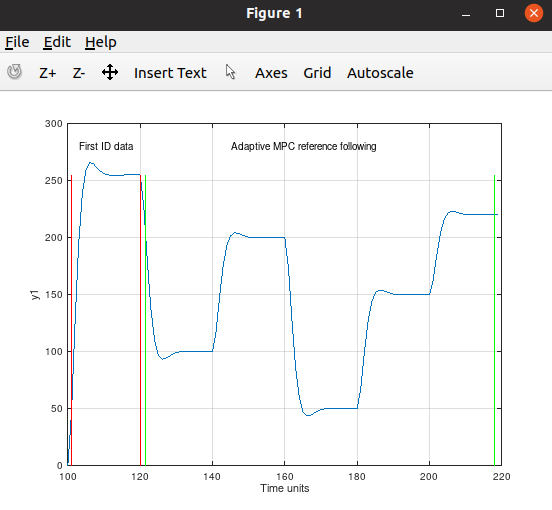
First order system (no change in the parameters for MPC):

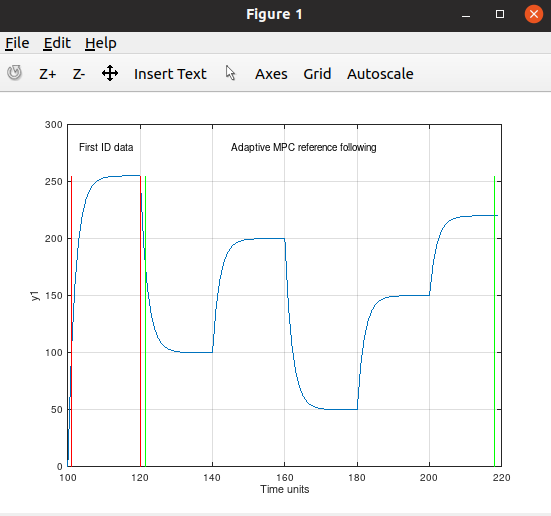
Second order with heavy time varying damping. It still tune in and follow the reference:

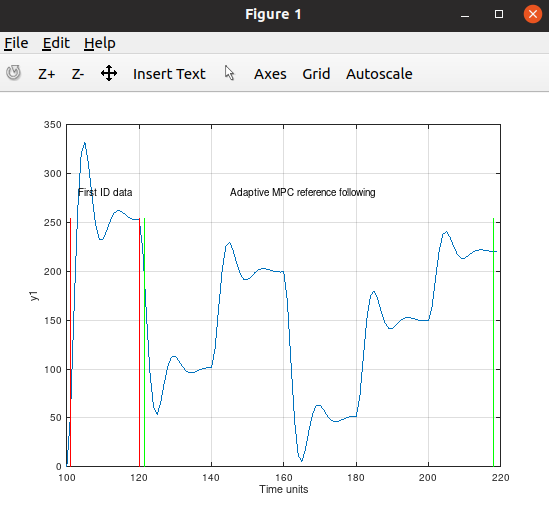
Second order with heavy time varying inertia.

The weakness of this MPC controller have is when it becomes radical changes for the static gain, like a mechanical spring changes its stiffness or a large watertank got extra or less isolation to prevent/increase e.g temperature leaks, or a capacitor changes its capacity. But if the mass of the spring changes, or the density of the water changes or the viscosity of the water changes or the electronic circuit changes its resistance or the coil got changes for the inductance, the adaptive MPC controller will handle it.