EMA for BCH (part 2)

[zawy12]

In a previous issue I discussed this in a different way, received feedback from Mark L, and discussed the possibility of RTT for BCH. This issue discusses everything that came up in a live stream and everything I know of surrounding changing BCH's difficulty algorithm (DA).

My process to find the "best algo" is this: find a window size parameter "N" for each algo that gives them the same standard deviation for constant HR. This indicates they accidentally attract on-off mining at the same rate. Then simulate on-off mining with step response that turns on and off based on a low and high difficulty value. I have "% delayed" and "% blocks stolen" metrics. Delay: add up a delay qty that is (st - 4xT) for each block over 4xT. Divide that by total blocks to get a % delayed. For "% stolen" I divide time-weighted target that the on-off miner sees by that of dedicated miners. It's how much easier his target was, while he was mining. I just now re-tested 5 DAs. Except for SMA-144, the other 4 below are pretty much the same. WT-190 has slightly lower % stolen but slightly higher delays. (WT-144 is what I kept mistakenly calling wtema in the video). Delays and % stolen are usually a tradeoff. I had been penalizing WT-144 in the past by giving it the same N as LWMA when it needs a larger value.

SMA-144 WT-190 (as opposed to wt-144) LWMA -144 ASERT / EMA - 72 [ update: See my 2nd comment below. In Jonathan's code, this value would be called 72 * ln(2) ]

I'll advocate the following for BCH in order of importance.

• ASERT or wtema with N=150 [ correction: this would be 150 * ln(2) in Jonathan / Neil's code ]
• Remove 1/2 timespan limit & do not add anything that limits how fast D rises (to prevent the unlimited blocks exploit).
• FTL 300 seconds with peer time removed or set it to FTL/2 instead of 70 minutes.
• No median of 3.
• 7xT limit on solvetimes to prevent spam attack

There's also sequential timestamps which might be the hardest to do in reality, but important on a theoretical level. It might be possible to enforce sequential timestamps by making MTP=1 instead of 11. Maybe this could prevent bricking of equipment. Sequential stamps (+1 second) must then be able to override local time & FTL. Overriding local time to keep "messages" (blocks) ordered messages is a requirement for all distributed consensus mechanisms. MTP does this indirectly.

Antony Zegers did some EMA code, using bit-shift for division.

EMA is a close enough approximation to ASERT, but here's Mark's tweet on how to do accurate integer-based e^x. https://twitter.com/MarkLundeberg/status/1191831127306031104?s=20

wtema simplifies to:
target = prev_target * (1 + st/T/N - 1/N) where N is called the "mean lifetime" in blocks if it were expressed as ASERT, target = prev_target * e^(st/T/N - 1/N) The other form of ASERT should give the same results, but the other form of EMA could return a negative difficulty with a large st. [ wtema-144 and asert-144 refer to N = 144 / ln(2) = 208.

If wtema is used: Negative solvetimes (st) are a potential problem for wtema if N is small and delays are long and attacker sends an MTP timestamp. See wt-144 code for how to block them. To be sure to close the exploit, you have to go back 11 blocks. Do not use anything like if (st < 0) { st = 0 } in the DA which allows a small attacker to send difficulty for everyone very low in a few blocks by simply sending timestamps at the MTP.

Std Dev of D per N blocks under constant HR for EMA/ASERT is ~1/SQRT(2*N). This is important for deciding a value for N. If HR increases 10x based on 10% drop in D, you definitely want N > 50 or the DA is motivating on-off mining. On the other hand, being at the edge of motivating on-off mining can reduce the expected variation in D. BTG's Std Dev is about 0.10 when it would have been 0.15 if HR was constant (N=45 LWMA, N=22.5 in ASERT terms). So it's paying a little to on-off miners to keep D more constant. ASERT with N=72 is same as SMA=144 in terms of D variation when HR is constant.

On the other side is wanting a sufficiently fast response to price changes. As a starting point, for ASERT N=100 it takes 6 blocks to rise 5% in response to a 2x increase in HR. This seems sufficiently fast. Std Dev is 1/SQRT(2*100) = 7% per 100 blocks which seems high. 5% accidental changes in D seems to motivate substantial HR changes, so maybe N=200 is better which will have 5% variation per 200 blocks. But this is like LWMA N=400 which would be incredibly smooth and nice if it works but this is 3x larger than my experience. BTG is very happy with LWMA N=45 with Std Dev 10%. Notice that there's bigger bang for the buck with lower N due to the 1/SQRT(N) verses N. You get more speed than you lose stability as you go to lower N. So instead of 200, I would go with 100 or 150.

None of the 60 or so LWMA coins got permanently stuck. About 5% could not get rid of bothersome oscillations. When sending the same random numbers to generate solvetimes, LWMA / EMA / ASERT are almost indistinguishable, so I do not expect them to get stuck either. Most LWMA's are N=60 which has the stability of EMA with N=30. N=100 would have probably been a lot nicer for them, if not N=200 (ASERT N=100). They are mostly T = 120 coins, so they have very fast response, reducing the chances of getting stuck.

Mark was concerned about forwarded timestamps sending difficulty very low which could allow a small attacker to do a spam attack (he would begin with setting a far-forwarded stamp for EMA/ASERT for submission later). To make this a lot harder to so, use st = min(st, 7*600). So long delays will not drop the difficulty as much as "it wants to". Most LWMA's do this as an attempt to reduce oscillations but it may not have helped any.

Combining upper and lower limits on difficulty, timespan, or solvetimes like the 4x and 1/4 in BTC, and the 2 and 1/2 in BCH is what allows unlimited blocks in < 3x the difficulty window. I'm the only one I know of that has described it. A couple of coins following me were the first to see it, losing 5,000 blocks in a couple of hours because I had the hole in LWMA but did not realize it. Some LWMA's had symmetrical limits on st, not just the 7xT upper limit. Removing the 1/2 limit on timespan in BCH will prevent it.

If FTL is dropped, the 70 minute revert from peer to local time rule should be removed (best) or set it to FTL/2 or less. It should be coded as function of FTL. There are a couple of exploits due to Sybil or eclipse attacks on peer time.

A pre-requisite for BFT is that all nodes have a reliable clock that has higher security than the BFT. The clock in POW is each node operator knowing what time it is without needing to consult the network. Any node can unilaterally reject a chain if its time is too far in the future so it's impervious to 99.99999% attacks. (Although current mining on honest chain needs to be > 50% HR of the forwarded cheating chain for the node to continue to reject the cheating chain because time going forward can make the cheating chain become valid.)

[jtoomim]

I've added ASERT to my fork of the kyuupichan difficulty test suite. This test suite allows for testing different algorithms with the same random seed (@zawy12, do I remember correctly that your suite uses a different random seed each time?). Unsurprisingly, ASERT performs basically identically to WTEMA on all metrics. The only differences between the two are small enough to be explained by rounding errors.

http://ml.toom.im:8051/ https://github.com/jtoomim/difficulty/blob/comparator/mining.py#L313

Also, here's Mark Lundeberg's paper about ASERT:

http://toom.im/files/da-asert.pdf

[zawy12]

Recently I have used the same seed to compare better. The code is "test_DAs.cpp" in the code section but it may be difficult to figure out how to use. Some of the mess is because it supports some RTT testing. It's written in terms of difficulty for CN coins.

You're heavy into testing and my 2nd paragraph is important, so I'll repeat it in a different way. The goal in testing is to choose a balance between 1) accidental variation that will not attract on-off mining and 2) speed of response to HR changes. You can't get both because lower variation comes with higher SQRT(N) and speed of response comes with lower N. So to compare algos fairly, you decide on an acceptable variation under constant HR and find the N for each algo that achieves it. Then you compare their the speed of response to step functions. Ability to rise fast means the on-off miner has less excess profits. The ability to come down fast means there will be fewer delays (and helps "dedicated" miner profits). You check speed of rising and speed of falling because some algos are good at one but not the other. You also check avg solvetime because if it's higher than the others, the algo is getting an unfair advantage.

So, I have the following algorithms with their N parameters chosen to give the same Std Dev under constant hashrate. This is in order from worst to best in terms of blocks stolen. Again, only SMA is significantly different from the others. WT wins but at a cost in delays.

SMA-144 (no median of 3) EMA - 72 (wtema form) ASERT - 72 LWMA - 144 WT - 190

Here are charts for the above. This is with 6x HR on-off simulating last years oscillations.

[jtoomim]

Edit/Note: The data presented in this comment are obsolete, due to incorrect window size settings. Accurate data can be found in this comment instead.

Here's some more data from an unpublished version of my sim. I added a proper LWMA. I notice that it takes a 240-block half-window LWMA (480-tap filter) to have the same responsiveness as ASERT-144 or WTEMA-144. ASERT and WTEMA perform identically, so I didn't include both at all N values.

CW-144 is awful, as expected -- steady-hashrate miners earn 13% less by mining BCH instead of BTC. WT-144 and WT-190 (or WHR as you call it?) are mediocre in this test. I'm curious why it performs worse in my testing than in yours. Everything else is pretty competitive, with the EMAs and LWMA at 288 blocks performing slightly better than other window sizes.

Profitability of different mining strategies

Alg	Greedy	Variable	Steady
asert-144	-0.02%	-0.001%	-0.579%
asert-288	0.01%	-0.001%	-0.463%
wtema-288	0.02%	-0.001%	-0.465%
wtema-576	0.06%	0.001%	-0.620%
lwma-190	-0.04%	-0.001%	-0.624%
lwma-240	-0.00%	-0.002%	-0.539%
lwma-288	0.01%	-0.002%	-0.482%
lwma-576	0.03%	-0.001%	-0.515%
wt-144	-0.03%	-0.011%	-2.128%
wt-190	-0.07%	-0.005%	-1.505%
cw-144	0.86%	0.131%	-13.129%

Zoomed:

The WT algos have weird glitchy excursions, like at blocks 7365 and 7422, which are completely absent from the other algorithms.

Parameters: 20k blocks, 300 PH/s steady HR, 10 EH/s variable, 1 EH/s greedy. Greedy threshold 3%.

[jacob-eliosoff]

Three quick comments:

1. For production use, avoiding floating-point math (like e^x) is probably pretty important, to avoid hardware dependencies leading to consensus failures. I understood this to be a major argument for @dgenr8's wtema.
2. The same numerical window parameter (eg 144) implies different responsiveness for EMA-type algos than for simple fixed-window algos, as noted previously. I think the code already accounts for this properly though: eg, mapping asert-"144" to IDEAL_BLOCK_TIME * 208, since 144 / ln(2) ≈ 208. That is, passing a "window" of 208 to asert should yield an algo similarly responsive to a traditional 144-block (1-day) moving avg.
3. As discussed briefly on the DAA livestream, whether to give longer blocks more weight in the weighted avg is important. As best I can recall, it's important that longer blocks not be given more weight, since that would lead to badness like 19 1-minute blocks and one 19-minute block weighted-averaging to 10 minutes.

[zawy12]

I did not realize the numbers in wtema-144 and asert-144 were "half lives" instead of the actual tau/T and alpha_recip inputs.

To compare the DA's fairly, do runs like this: N = alpha_recip = tau/block_time = mean lifetime = half-life / ln(2) ASERT = EMA = N (e.g. N = 288/ln(2), 144/ln(2), or 72/ln(2) ) LWMA = SMA = 2 * N (to my surprise they have the same StdDev for a given N) WT = 2 * N * 190/144

Once you decide a winner after testing for this particular N, that DA will very likely always be your winner for any consistent change to N which means it will always be your winner.

My LWMA and ASERT runs above show it's very difficult to see any difference between them which indicates this "matching Std Devs" method is good.

The WT glitch you see should go away once you give it this higher N. I just checked my WT (WHR) code and your WT code and they should be the same.

The Weighted Harmonic in these names refers to the calculation on the D/st values which is mathematically the same as Tom's target * time code. LWMA is avg(D) / weighted_mean(st) so I dropped the "WH".

For production use, avoiding floating-point math (like e^x)

Mark's tweet solves the hard step in implementing an integer based e^x, although it may take a little work to figure out how to use what he said in a complete e^x. But as we know, for large N, wtema will be the same.

[zawy12]

Once you settle on a given set of assumptions that lead to a given set of tests, then you can apply the tests to all the algos. You have to also have a metric for success. Mine is that the winning DA is the one with the least % stolen plus % delays under all on-off settings of different sizes of HR "attacks" and different starting / ending percentages of a baseline D. You make an initial guess for N as I define it above. After your tests indicate a winner for that N, you use that DA for different N's. Once you find an optimum N for that DA, there should be no other DA for any other N that will give a better result. This is if you do not change your tests and metric and if my theorizing and your testing are both correct (or equally wrong). But my charts above show LWMA, EMA, and ASERT for N>30 are basically the same thing. WT is detectably a little different.

BTW, Digishield's N in terms of SMA / LWMA needs to be N/4 due to it "diluting" the timespan by 4. The Std Dev confirms this. For SMA N=144, this is Digishield N=36 instead of N=17. Here's the same conditions above to compare ASERT and Digi N=36. "Improved" means the ~6 block MTP delay has been removed to help Digishield perform better. Default Digishield would have been 2x worse for BCH than CW-144. Digishield is an "SMA inside of an EMA" with N=4. target = avg_17_targets * (1 + avg_17_st/T/4 - 1/4) (but the 17 solvetimes here are shifted ~6 blocks in the past which makes the oscillations very consistent)

[jtoomim]

I'm not too worried about the floating point issue. It's a mild annoyance to construct a MacLaurin or Taylor series for e^x or 2^x, but it's definitely doable. @jacob-eliosoff I used float math in my initial python asert implementation out of laziness and the desire to get the algo working quickly, not because I intend that to be how it would finally be implemented in C++. I'll fix it soon-ish.

As I see it, the wtema vs asert debate centers on the following issues:

1. Integer approximations -- easier with wtema than asert, but possible in both
2. Singularity and negative solvetimes -- problematic with wtema, but not asert. wtema likely needs rules restricting solvetimes to be greater than some value (e.g. > -0.5 * 144 * 600 sec for wtema-144)
3. Mathematical and theoretical elegance -- good with both, but better for asert
4. Accumulation of rounding/approximation error -- modest in wtema, but absent in asert due to its absolute nature

Any other considerations that I'm missing?

The WT glitch you see should go away once you give it this higher N. I just checked my WT (WHR) code and your WT code and they should be the same.

Ah, yes, I see the issue. The WT code was treating N as the window size, whereas the LWMA and EMA code was treating N as the half-life or half-window size. Will fix.

[jtoomim]

With fixed N for wt, and sorted by N, and with bold for the winner at any given N:

Profitability of different mining strategies

Alg	Greedy	Variable	Steady
asert-144	-0.02%	-0.001%	-0.579%
lwma-144	-0.07%	-0.000%	-0.927%
wt-144	-0.05%	-0.001%	-0.648%
lwma-190	-0.04%	-0.001%	-0.624%
wt-190	-0.01%	-0.001%	-0.539%
lwma-240	-0.00%	-0.002%	-0.539%
asert-288	0.01%	-0.001%	-0.463%
wtema-288	0.02%	-0.001%	-0.465%
lwma-288	0.01%	-0.002%	-0.482%
wt-288	0.02%	-0.001%	-0.471%
asert-576	0.06%	0.001%	-0.616%
lwma-576	0.03%	-0.001%	-0.515%
wt-576	0.05%	0.001%	-0.597%

Edit: fixed N values a second time

Edit2: I'm going to change this again

[jtoomim]

asert-144: 'tau': (IDEAL_BLOCK_TIME * 208) wtema-144: 'alpha_recip': 208 lwma-144: 'n': 144*2 wt-144: 'block_count': 144*2 * 190 // 144

These tests results are from code that isn't on my repo yet.

You need wt576 * 190/144 = 760

The most recent data includes that.

Edit: I'm changing most of these in a second.

[zawy12]

N = alpha_recip = tau/block_time = 144/ln(2) = 208 N_lwma = N_sma = 2 * N = 416 N_wt = 2.64 * N = 549

[jacob-eliosoff]

@jtoomim, definitely not criticizing your implementation, but it is strongly preferable that the algo fundamentally not depend on floating-point. Yes there are integer-math approximations, but they add computation steps and, above all, complexity (in the plain English sense), leading to 1. greater risk of bugs/exploitable cases and 2. bikeshedding - there are many possible approximations.

The simpexpi/emai/emai2 algos were my stabs at integer-math approximations of simpexp (aka asert)/ema/ema2, but once I saw Tom's 2-line wtema I much preferred it. I rate simplicity as a top criterion here. (There may be equally simple integer-math algos which approximate asert even better: those to me would be wtema's real competition.)

[jtoomim]

Okay, new settings for N etc:

wt-144: 'block_count': 144*2
lwma-144: 'n': 144*2,
asert-144: 'tau': (IDEAL_BLOCK_TIME * 144),
wtema-144: 'alpha_recip': 144, 

These settings result in the step response for all four algorithms clustering closely for each responsiveness setting:

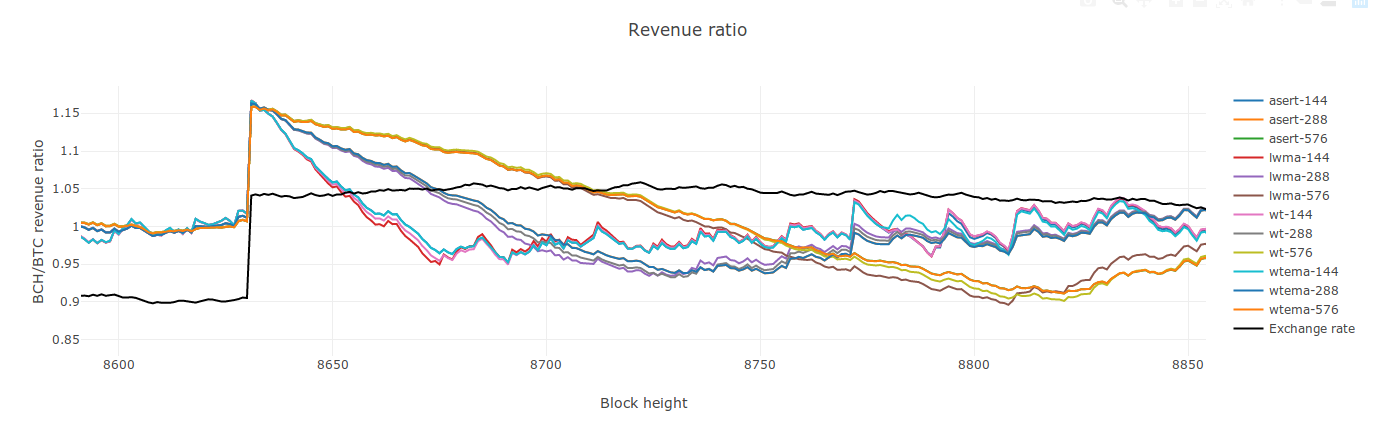
N_wt = 2.64 * N = 549

This seems wrong. Including the extra 32% (190/144) seems to mess it up. If I use that 32% factor, WT ends up as a clear outlier on the impulse response. I've removed it.

[jacob-eliosoff]

@jtoomim looking good! Apples-to-apples.

[jacob-eliosoff]

I suspect this is immaterial but 576 maps more closely to 831 than 832: 576 / ln(2) = 830.99. For testing purposes you could even maybe pass in floating-point windows just to make sure these diffs aren't distorting the comparisons, dunno...

[jacob-eliosoff]

Also to be very clear, the algo of Tom's I've been praising since I saw it is wtema (eg wtema-144), not wt (wt-144). As I recall I considered wt pretty flawed (also, needlessly messy with its for loop etc) - a little surprised it's not performing worse in these tests.

[jtoomim]

Confirmation times

Algorithm	Block interval (sec)	Confirmation time (sec)
asert-144	599.79	753.62
wtema-144	602.98	757.14
lwma-144	600.36	755.05
wt-144	603.23	761.64
asert-288	599.59	672.23
wtema-288	601.02	673.50
lwma-288	600.17	673.10
wt-288	601.22	676.09
asert-576	599.06	667.28
wtema-576	599.98	661.51
lwma-576	600.03	671.99
wt-576	600.27	673.36
cw-144/2	608.88	1565.14

The confirmation time is the expected amount of time needed to confirm a transaction issued at a random time. This is greater than the average block interval because a random instant is more likely to be in a long block interval than a short one.

Profitability of different mining strategies

Algorithm	Greedy	Variable	Steady
asert-144	-0.043%	0.011%	-0.699%
wtema-144	-0.047%	0.011%	-0.693%
lwma-144	-0.027%	0.010%	-0.720%
wt-144	-0.036%	0.010%	-0.721%
asert-288	-0.007%	0.008%	-0.333%
wtema-288	-0.007%	0.008%	-0.333%
lwma-288	-0.006%	0.008%	-0.348%
wt-288	-0.006%	0.008%	-0.348%
asert-576	0.014%	0.004%	-0.290%
wtema-576	0.016%	0.004%	-0.286%
lwma-576	0.015%	0.004%	-0.305%
wt-576	0.016%	0.004%	-0.305%
cw-144/2	1.245%	0.259%	-10.899%

cw-144/2 is a 144-block window, equivalent in impulse response to lwma-072.

[jtoomim]

@jacob-eliosoff wt-144 was performing poorly until I changed the window size from 144 blocks to 288 blocks. That is, I made "144" the half-window size, just like it is for LWMA and half-life for EMA. With this change, it performs about as well as LWMA and EMA. I'm not seriously considering it as the next BCH DAA. I've mostly only been including it in the analysis because zawy12's analysis showed it to be much better than my initial analysis did, which was a discrepancy that was worth investigating and fixing.

I agree: floating point math is bad. However, the main cost of wtema's use of addition instead of exponentiation is that wtema has a singularity when block_time == -IDEAL_BLOCK_TIME * (alpha_recip - 1). This singularity is an externalized complexity cost. It requires additional lines of code elsewhere to forbid negative solvetimes, or to bound solvetimes within a narrower range. An integer version of asert could avoid that singularity and avoid the need to change the MTP-11 rule. I suspect this would save more lines of code elsewhere than it takes to implement the integer asert approximation.

I'll take a closer look at your simpexpi/emai/emai2 soon.

[zawy12]

Notice asert can't be seen because it's always exactly under wtema, except a little after block 5780 8780 where wtema-144 jumps away from the others (which needs to be investigated).

The "equivalent std dev" numbers I gave are barely to 2 significant figures and since the only difference above is mostly in the in the 3rd significant figure, it's still hard to determine if any is better than the others.

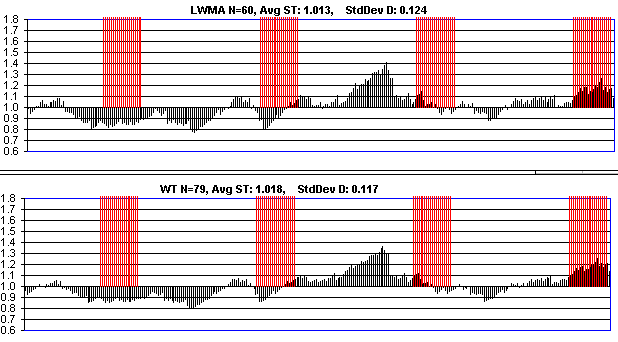
It's a mystery that your lwma and wt need the same N. I have two completely different programs that show N_wt = 190/144 * N_lwma gives the same std dev (constant HR) and look nearly identical to step responses like this:

[jacob-eliosoff]

@jtoomim, your comments on wt-144 and wtema vs asert all make sense to me.

I didn't spend a lot of time on the integer math hacks in simpexpi etc so I wouldn't be surprised if @markblundeberg's approximation is more robust.

The confirmation time is the expected amount of time needed to confirm a transaction issued at a random time. This is greater than the average block interval because a random instant is more likely to be in a long block interval than a short one.

Hmmm. It seems to me that with stable hashrate, the expected confirmation time should be exactly 10 minutes. (You're more likely to start waiting during a long block than a short one; but you also start on average halfway through the block rather than at its beginning, and these two factors are supposed to exactly balance out.) Maybe what this reflects is that when hashrate and thus difficulty adjusts, block times get more likely to be very long (also very short but that's irrelevant), which bumps up confirmation times for the reason you described? So, the more hashrate shenanigans, the higher the expected conf time?

[jtoomim]

with stable hashrate, the expected confirmation time should be exactly 10 minutes. ... the more hashrate shenanigans, the higher the expected conf time?

Yes, that's correct. If I get rid of the switch miners, confirmation times get very close to 600 seconds (+/- 1.2%) for all algorithms. I'm using confirmation time as a summary metric of how much the block intervals deviate from an ideal Poisson process.

[jtoomim]

Notice asert can't be seen because it's always exactly under wtema, except a little after block ~~5780~~ 8780 where wtema-144 jumps away from the others (which needs to be investigated).

That's probably just the greedy hashrate switching off slightly earlier for wtema-144 than for the other algorithms. Prior to that jump, wtema-144 was ever so slightly lower than lwma-144 and asert-144, which means the revenue ratio could have fallen below the 1.03 threshold for the 1 EH/s of greedy hashrate one block earlier. That, in turn, could have resulted in one or two unusually long block intervals, triggering the following jump in profitability.

[zawy12]

Your metric implies the larger the N, the better. There must be some counter-force to that. There needs to be a metric that balances the need for stability (high N) with the need to respond quickly to BTC/BCH price variation (low N). My intuitive assumption has been that we want to set N so that accidental variation is equal to the expected price variation (both in % per day). If we want accidental variation to be 1/2 of price variation, then we would need N to be 4x larger which would make it 4x slower to respond to price changes.

[jtoomim]

Your metric implies the larger the N, the better.

No, it implies that the optimum N is near or above the high end of the range that was tested.

Confirmation times

Algorithm	Block interval (sec)	Confirmation time (sec)
asert-144	599.80	815.30
asert-288	599.59	687.08
asert-342	599.51	681.79
asert-407	599.41	677.11
asert-484	599.28	680.00
asert-576	599.13	705.52
asert-685	598.94	685.50
asert-815	598.71	749.85
asert-969	598.46	710.08
asert-1152	598.20	748.44
asert-2304	596.89	907.92

Profitability of different mining strategies

Algorithm	Greedy	Variable	Steady
asert-144	-0.107%	0.011%	-0.820%
asert-288	-0.011%	0.005%	-0.361%
asert-342	-0.003%	0.004%	-0.329%
asert-407	0.003%	0.002%	-0.311%
asert-484	0.001%	0.002%	-0.307%
asert-576	0.003%	0.003%	-0.318%
asert-685	0.025%	0.002%	-0.318%
asert-815	0.024%	0.002%	-0.352%
asert-969	0.033%	0.003%	-0.381%
asert-1152	0.036%	0.004%	-0.423%
asert-2304	0.094%	0.007%	-0.724%

[dgenr8]

@jacob-eliosoff I stressed in the livestream the importance of not confounding a blocktime with any prior difficulty other than the one at which that block was mined. The original BTC algo, wtema, ema, wt, and asert all have this property (in the case of asert, it's because no prior difficulties are referenced at all). cw and lwma do not have this property.

@jtoomim Nice to see the step function test. I agree with @zawy12 that both direction of step function should be tested. The magnitude of the profitability step should be at least as extreme as anything ever seen over the space of an hour or so.

[zawy12]

Why is greedy so low? Using last year's miner motivation simulation (6x HR if D is 1.30x baseline HR's needed D and turning off at 1.35x) and if BTC/BCH price is a constant, I see greedy miners with ASERT-484 getting 1% higher target/time (1% more profit) for 1/3 of the blocks (compared to constant miners) and all miners averaging 2.5% profit per block from the slower solvetime. With ASERT-144, the greedy get 1.7% higher target for 1/3 of the blocks but there is not the additional 2.5% lower solvetime being paid out to all miners.

My old LWMA N=60 under these conditions has correct solvetime, but this on-off miner scenario gets 7.7% higher target for 1/3 of the blocks. LWMA is also 1.7% at N=288 (ASERT N=144), so it seems I chose N 1/4 or 1/5 of what he needed to be for a lot coins.

[jtoomim]

Why is greedy so low?

Probably because in my simulation, most of the equilibration is done by the variable category, which will switch hashrate between both chains in a memory-ful and proportional (vs instantaneous all-or-none) fashion. This emulates the behavior of pools like Bitcoin.com, and also emulates the behavior of an aggregation of many different greedy miners with different thresholds. With proportional miners and a good DAA, greedy miners rarely get a chance to turn on even if their threshold is as low as 3% higher profitability, as it is in my simulation. A while ago, rinexc did an analysis of BTC.top's and Unknown's greedy mining strategies, and found them to switch at 3% and 5% higher profitability, respectively.

I spent about 5 hours tweaking the variable hashrate algorithm to try to make it model the behavior of an aggregate of self-interested miners. I don't think I succeeded perfectly, but it works much better than the original kyuupichan variable algorithm, and actually ensures that profitability remains close to 1.0 most of the time, and usually within ±3% of 1.0. But it doesn't prevent the CW oscillations at all.

[jtoomim]

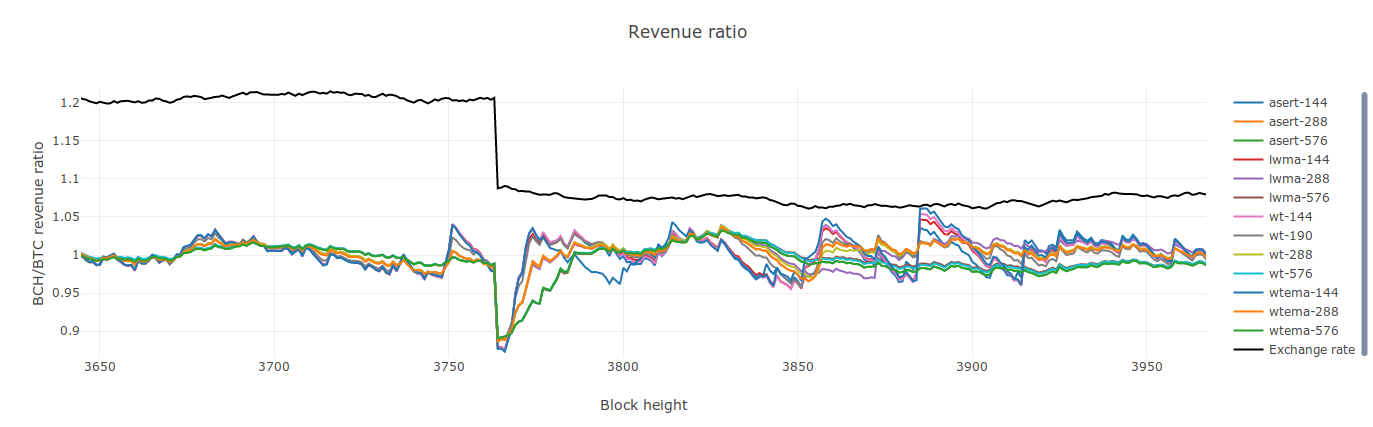
both direction of step function should be tested.

@dgenr8 Both directions are tested by the code. I had just zoomed in on a positive step in the screenshot. Here's a negative step for you:

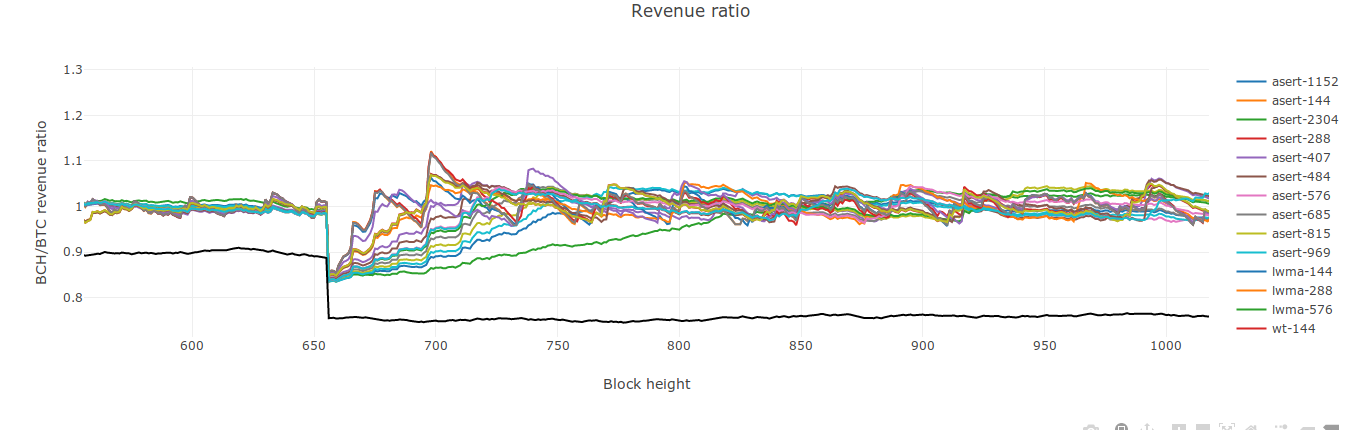
And here's another one, but with a wider range of ASERT N values so you can taste the rainbow:

I've also pushed my LWMA etc code and updated http://ml.toom.im:8051/, so if you want to look at positive and negative steps in more detail, you can do so there. Or, even better, run a copy locally for better performance. It gets pretty laggy when you have a half dozen algorithms with more than 5k blocks each.

[zawy12]

I can't understand the inputs to your form very well. My simple method has been able to mimic all the oscillations I've seen. I never thought to try modelling the effect of random changes in exchange price. This might be partly because I want to make random D variation equal price variation. So when I model the effects of miner motivation on random D variation, it's same as price variation if D were constant. So I'm missing the effect of the combination.

[jacob-eliosoff]

I don't have a strong sense of the tradeoffs of high N (stability) vs low N (responsiveness). Qualitatively, excessive stability is dangerous because 1. it leads to more "incorrectly cheap/expensive" blocks when hashrate/price moves around; and 2. a plunge in hashrate (eg post-split) could take days/weeks to recover from, if at all, one of the more realistic "chain death" scenarios. Whereas excessive responsiveness leads to noisy swings in difficulty, which 1. may increase frequency of long confirmations when difficulty bumps too high sometimes, and 2. may be easier for miners to game (though all the good algos here should greatly reduce that).

@jacob-eliosoff I stressed in the livestream the importance of not confounding a blocktime with any prior difficulty other than the one at which that block was mined. The original BTC algo, wtema, ema, wt, and asert all have this property (in the case of asert, it's because no prior difficulties are referenced at all). cw and lwma do not have this property.

@dgenr8, was this in response to something I said above? I'd think the nearer an algo is to a pure (memoryless) EMA, the less it should depend on difficulties (or even block times) before the last. So I'm all for avoiding these dependencies when possible.

[dgenr8]

@jacob-eliosoff As you seem to imply, noisy difficulty itself is not a problem, extreme blocktimes are. The tips of the tightrope walker's pole move crazily so that he can remain steady. This is seen with RTT.

You said something about weighting longer times more heavily. I guess it was in reference to something else. Anyway, I agree with you -- that is not justified!