tonality analysis

[shichaog]

Hi, FFT for calculating tonality in analysis.c file.

    for (i=0;i<N2;i++)
    {
 //Why assign real number(audio sampled points) to image parts for FFT?
       float w = analysis_window[i];
       in[i].r = (kiss_fft_scalar)(w*tonal->inmem[i]);
       in[i].i = (kiss_fft_scalar)(w*tonal->inmem[N2+i]);
       in[N-i-1].r = (kiss_fft_scalar)(w*tonal->inmem[N-i-1]);
       in[N-i-1].i = (kiss_fft_scalar)(w*tonal->inmem[N+N2-i-1]);
    }
and then:
    opus_fft(kfft, in, out, tonal->arch);

tonal->inmem is 10ms smoothed input float point audio data(Total length is 30ms). So Why assign real number(audio sampled points) to image parts for FFT? and what does FFT out spectrum mean? could some one help？

Thanks!

[silverbacknet]

That's just a KISS FFT thing ( https://github.com/mborgerding/kissfft ), if you pack half into real and half into imaginary it'll parallelize the processing. I have to wonder how much a naive memory copy like this hurts versus how much the parallel helps, but it's so fast it might not even be measurable anymore.

The out has the real and imaginary as you'd expect, see above or just the code in the opus sources for details. They're unscaled. (Thus the window scaling while reading into the buffers.)

[shichaog]

That's just a KISS FFT thing ( https://github.com/mborgerding/kissfft ), if you pack half into real and half into imaginary it'll parallelize the processing. I have to wonder how much a naive memory copy like this hurts versus how much the parallel helps, but it's so fast it might not even be measurable anymore.

The out has the real and imaginary as you'd expect, see above or just the code in the opus sources for details. They're unscaled. (Thus the window scaling while reading into the buffers.)

For above loop, N=480, N2=240, that is doing 480 sample FFT, all sampled samples are stored in tonal->inmem[i], whith 10ms smooth.

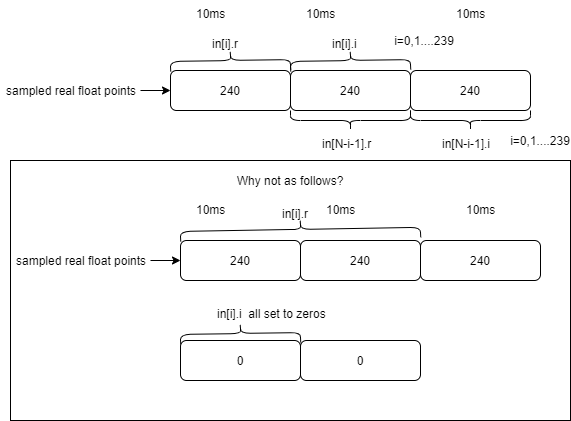
as show in above picture, why 480 points not use just front 20ms data? and I try 480 and 720 point real fft, the results is not equal to opus_fft results. Could you help explain more detail? thansks @silverbacknet