How do we want to implement mesh stretching (for the cubed sphere mesh)?
While the P4estMesh supports local mesh refinement and AMR, this can be problematic for complex simulations like the baroclinic instability. There, well-balanced errors make the simulation on a vertically non-conforming mesh unusable. Unfortunately, the P4estMesh doesn't support only horizontal refinement (yet?).
A simple way to avoid the problem of non-conforming meshes is to stretch the cubed sphere mesh smoothly towards the area that is to refine. A mapping for this is described here. This mapping is also used by FV3, the dynamical core of the Global Forecast System by the National Weather Service of the United States.
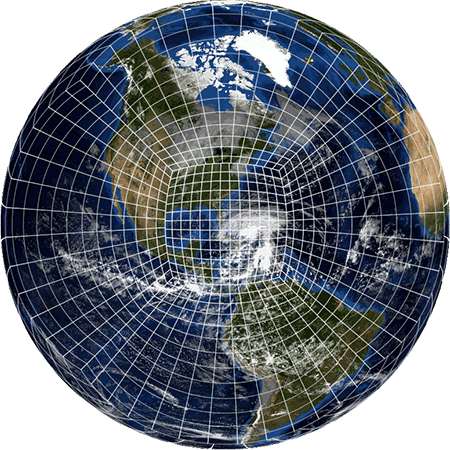
I already implemented this feature for Trixi:


However, now there's the question of how to include this feature in the API. Do we want to write this mapping into the P4estMesh constructor for cubed spheres and add a kwarg to set the stretching factor? Or do we want to allow passing arbitrary functions to transform the cubed sphere? In this case, do we want to add this option to the HOHQMesh constructor as well?
First of all, it's great to see that you're continuing the discussion (and implementation!) on this topic! My initial thought regarding your questions is to implement it in the simplest, probably more specific way (i.e., only for CS meshes), until something similar is needed for general meshes. Once someone has a second application for this kind of stretching, we already have two examples and it might be easier to get the API for general transformations right the first time.
OTOH, StructuredMesh and the structured P4estMesh constructor already support passing arbitrary mappings.
Also, while the stretching itself could be easily added as a kwarg to the constructor (stretch_factor=x), this stretch mapping only stretches the mesh towards the south pole. Then, the sphere has to be rotated to move the refined area to where it should be.
At first sight, I would say that it would be great to pass arbitrary mappings to transform the cubed sphere. Then, the current mapping of course works, but it would be possible to try out other things as well. Mappings are very powerful and cool to play around with (as you have demonstrated quite impressivley with this simulation).