Polynomial solver crashes with certain (quite reasonable) inputs
The following call never returns:
sym::solve_real_roots(sym::Polynomial<4> {1, 0, 0, 1, 1});
I tested with other quartic polynomials as well, and the crash seems to always happen when the second and third coefficients are zero and the other ones are not.
Hey, thanks for reporting this! I'll add it as a test case and figure out what's going wrong. Be right back!
I think I've fixed this in the latest commit ca9583c71116844d6dbd995ee931fefc248ea74b. I was incorrectly calculating upper bounds on the real roots using the zero coefficients. This should be fixed now. Note, the quartic polynomials are solved using an iterative technique by bracketing the roots with a Sturm chain. This means its not as fast as a quartic formula; however, there is no "general" and stable quartic formula, even though many particular solutions exist.
If you want a quartic formula, I've ported one here: https://github.com/toastedcrumpets/DynamO/blob/master/src/magnet/magnet/math/quartic.hpp Unfortunately the original site on the man who did all the work trying to figure out a good quartic implementation has now gone down and this is all that remains. If your application is not critical, then its a good, fast, unstable formula.
Thanks, it seems to be fixed now. I'm using it to find intersections between two closed loops of quadratic Bézier curves, and then dissolving the loops into one (or more in some cases) if they overlap. You can probably imagine this requires quite a bit of stability, but I'd also prefer to avoid iterative methods for performance reasons.
I found these two papers on the topic: https://www.researchgate.net/publication/262935349_A_universal_method_of_solving_quartic_equations https://www.researchgate.net/publication/291873816_A_simple_method_to_solve_quartic_equations
I didn't really look into them yet, but the first one seems to deal with the same algorithms as the code you linked, and the second one sounds pretty promising based on the abstract. As far as I'm aware, there are general ways of solving quartics analytically, and it's just a matter of making it numerically stable for all possible inputs.
Cool application and thanks for the papers! This was something I dived into far too much a while ago and I hadn't seen these. You have summarized the problem correctly, making it numerically stable is the fundamental issue. This is far trickier than most people realise. For example, consider just the quadratic solver I have: https://github.com/toastedcrumpets/stator/blob/master/stator/symbolic/polynomial.hpp#L784 If you compare it to the "normal" quadratic formula, you'll see the problem is not just catastrophic cancellation/round-off error, but also overflows.
The first paper you've linked on a "universal method" shows there are an arbitrary number of ways to solve the quartic equation and gives a general way to generate these which is really nice, but they do not discover how to choose the right approach to avoid numerical errors. The second paper gives another approach but no information on the numerical stability of it, which is the basic problem. So both of these papers do not address the fundamental issue of stability. Most people trying to solve quartics switch to Mathematica/Maxima/etc, and that uses infinite precision floats (rational numbers) which mean that any of the quartic formula will work, but this is much much slower than floats.
The method I'd implemented should (when it has no bugs) always give reasonable results when used with floats (and it does as far as I've tested). It might miss/find-extra roots arising from the initial transformation into a Sturm chain, but practically I've not seen that yet.
I would note the iterations done in my formula are fast (no dynamic allocation), and they are bisections, so they terminate quickly and have a max iteration. I would also note, that the stable implementation of Herbison-Evans, which is the current gold standard, still does iteration on the final roots to polish them, as they can drift from the original equation due to numerical error from the required transformations. That's why I only do a single transformation to a Sturm chain, it avoids accumulating error from repeated transformations.
In your position, I would give both a try. You'll probably find that my method is as-fast as the Herbison-Evans while also generally working better. Let me know how you get on!
I see, I'll consider using iterative methods as well. Before calculating the intersections between two curves, I can first check if their bounding triangles overlap, so the performance cost might not be that bad. I should also mention that the final algorithm needs to run on fixed-point arithmetic, which makes both overflows and rounding error harder to avoid.
However, it seems like even your current iterative algorithm isn't quite stable enough for what I'm doing. It does indeed find roots that don't actually exist, and misses some roots that do. Even though it only happens with a small fraction of polynomials, it still happens quite often when you move the curves freely with the mouse. Here are two examples:
sym::Polynomial<4> f =
{
14482.000000000001818989403545856,
-83591.999999999985448084771633148,
84887.999999999970896169543266296,
1.3022974889306702395208061776649e-11,
8.0779356694631608874161005084957e-28
};
sym::Polynomial<4> g =
{
35842,
-57720,
59799.999999999985448084771633148,
-5.2252677024996035907674102414044e-12,
2.0194839173657902218540251271239e-28
};
For f the algorithm finds no roots when there should be two, and for g it finds one root when there should be none. Here's a graph of them:
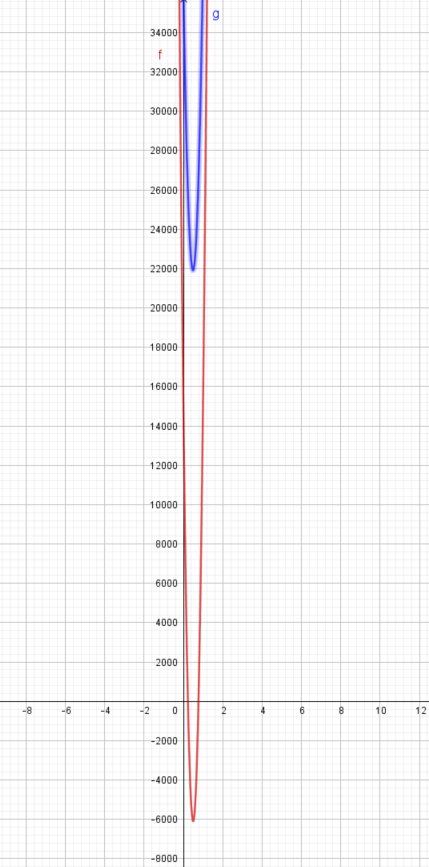
In both examples, the first three coefficients are relatively big compared to the other two, so it might be possible to fix it by clamping the smaller ones down to zero, but I'm not sure if that will fix the underlying problem for all cases.
Thanks again for more detective work. So your two examples are (just thinking out loud here) 14482.000000000001818989403545856-83591.999999999985448084771633148x+84887.999999999970896169543266296xx+xxx1.3022974889306702395208061776649e-11+xxxx8.0779356694631608874161005084957e-28 Which is this on wolfram alpha, showing two real roots: https://www.wolframalpha.com/input?i2d=true&i=14482.000000000001818989403545856-83591.999999999985448084771633148x%2B84887.999999999970896169543266296xx%2Bxxx1.3022974889306702395208061776649e-11%2Bxxxx8.0779356694631608874161005084957e-28 And 35842-x57720+xx59799.999999999985448084771633148-xxx5.2252677024996035907674102414044e-12+xxxx2.0194839173657902218540251271239e-28 Showing no real roots on wolfram alpha https://www.wolframalpha.com/input?i2d=true&i=35842-x57720%2Bxx59799.999999999985448084771633148-xxx5.2252677024996035907674102414044e-12%2Bxxxx2.0194839173657902218540251271239e-28
I'll check these in detail tonight to find out why they're not detected. My guess is numerical error in the bounds code, but it could also be the transformation to a Sturm chain. Regardless, thanks again for another failing point to check!
With fixed point arithmetic you are in serious trouble. You might be better starting with the generic quartic formula I linked before and then testing the cases for it?
OK I've confirmed this is an issue with the Sturm construction/solution. The bounds are correctly calculated. This might be hard to solve, there's lots of places that precision can be improved in polynomials. I'm guessing my polynomial evaluation could be improved, before I try improving the Sturm generation, which I think is probably OK. This is something I cannot fix quickly though, so I'll leave the issue open in the near term. Please keep me posted on your own work, its very interesting.
Notes for later. One issue with this is the loss of precision in polynomial evaluation. This paper has some excellent ideas around improving precision: https://arxiv.org/ftp/arxiv/papers/0805/0805.3194.pdf Need to implement this along with some test cases, then revisit
That's cool. In the meantime I discovered that when you convert the quadratic Bézier curves into implicit parabolas and change the coordinate system just the right way, you can find their intersections by first solving a quartic with no 3rd or 2nd degree terms and then a quadratic for the other coordinate. I didn't implement this yet but it would be a lot easier than solving a full quartic so I hope I'm not mistaken.
I'm also considering using integers instead of fixed point. Then there wouldn't be any rounding error as long as I only do addition, multiplication and subtraction. I'd also have to use enough bits (probably more than 64) to prevent overflows, but I think I can afford that since I can easily limit the input coordinates to 12 bits or less, maybe even just 8.
More notes while I work on this: An examination on how roots depend on the coefficients, just general background reading on polynomial precision https://www.skewray.com/articles/how-do-the-roots-of-a-polynomial-depend-on-the-coefficients
Glad to hear you're making progress too!