[WIP] experimental Laplace approximation

[jeffpollock9]

trafficstars

Hello, as per the discussion in #1178 I've started to code up how a Laplace approximation over a joint distribution could look. It's still very much WIP as these things are missing/I'm not sure about:

1. The design - do we want users to input a joint distribution and data? An alternative would be allowing them to create their own target log prob function like e.g. mcmc does? There is also the possibility of creating a LaplaceApproximation distribution class and use that instead of the current transformed MVN?
2. This doesn't work in eager mode without the tf.function annotation, I couldn't quite understand why. There are also (related?) issues with running this with jax and numpy modes so those tests fail. I can dig deeper into this but a small nudge in the right direction would really help.
3. The documentation needs to be written. I was hoping to do this last to avoid having to re-write if anything changes.
4. ~Add test or two that the hessian approximation recovers (approximately) the covariance~, and maybe a test that shows that providing different bijectors results in different Laplace approximations (which should probably be mentioned in the docstring).

@ColCarroll just tagging you as you said you would be happy to have a look - hope that is ok.

Thanks!

[jeffpollock9]

This looks great!

It'd be nice to see another test or two that the hessian approximation recovers (approximately) the covariance, and maybe a test that shows that providing different bijectors results in different laplace approximations (which should probably be mentioned in the docstring).

I guess the other TODO is filling out the docs for laplace approximation.

Let me know if you want help with any of this, or won't have time for a while -- this looks like some careful work, and I don't want it to get lost!

Cool!

Yes those sound like good tests, I'll add them to my TODO list at the top of the PR. If you think the API looks reasonable then I would be happy to start filling out the documentation? The main thing I need help with is figuring out what to do with this None gradient error that you get without the @tf.function annotation in TF mode or when running with jax (as mentioned above with an example) - so any input there would be amazing.

I should have some time for this here and there over the next couple of weeks.

[ColCarroll]

Hey @jeffpollock9 -- I used some of the ideas from your _transform_reshape_split bijector in the new windowed sampler -- (re) using some of that code might be helpful here.

[jeffpollock9]

Hey @jeffpollock9 -- I used some of the ideas from your _transform_reshape_split bijector in the new windowed sampler -- (re) using some of that code might be helpful here.

@ColCarroll cool, thanks for sharing, perhaps we can pull this out as a new bijector for all to use? I'm not sure when I'll get more time to spend on this stuff but I am sure I will get to it at some point. In the meantime if you'd like to edit any of my stuff in any way please feel free.

[jeffpollock9]

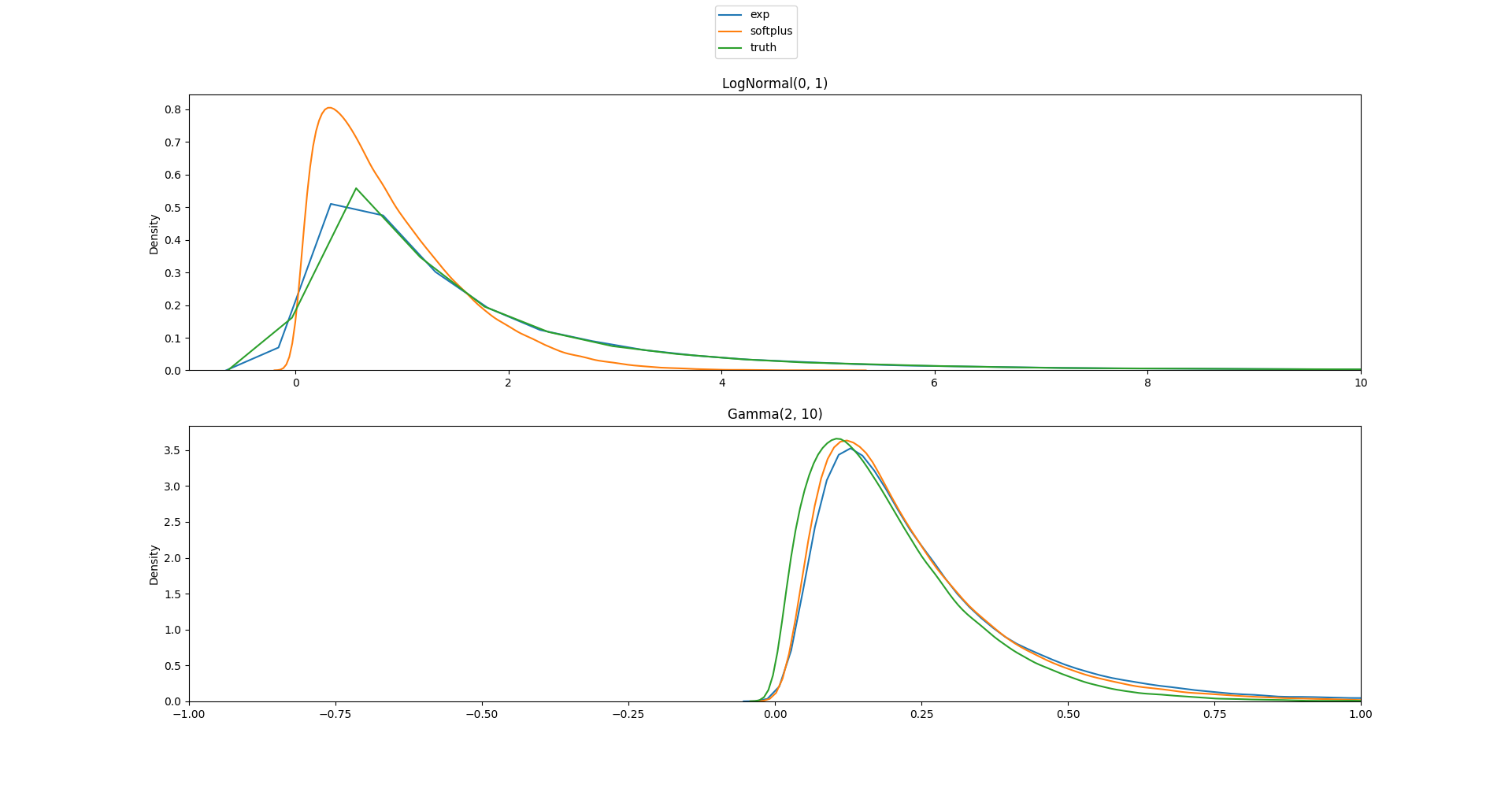
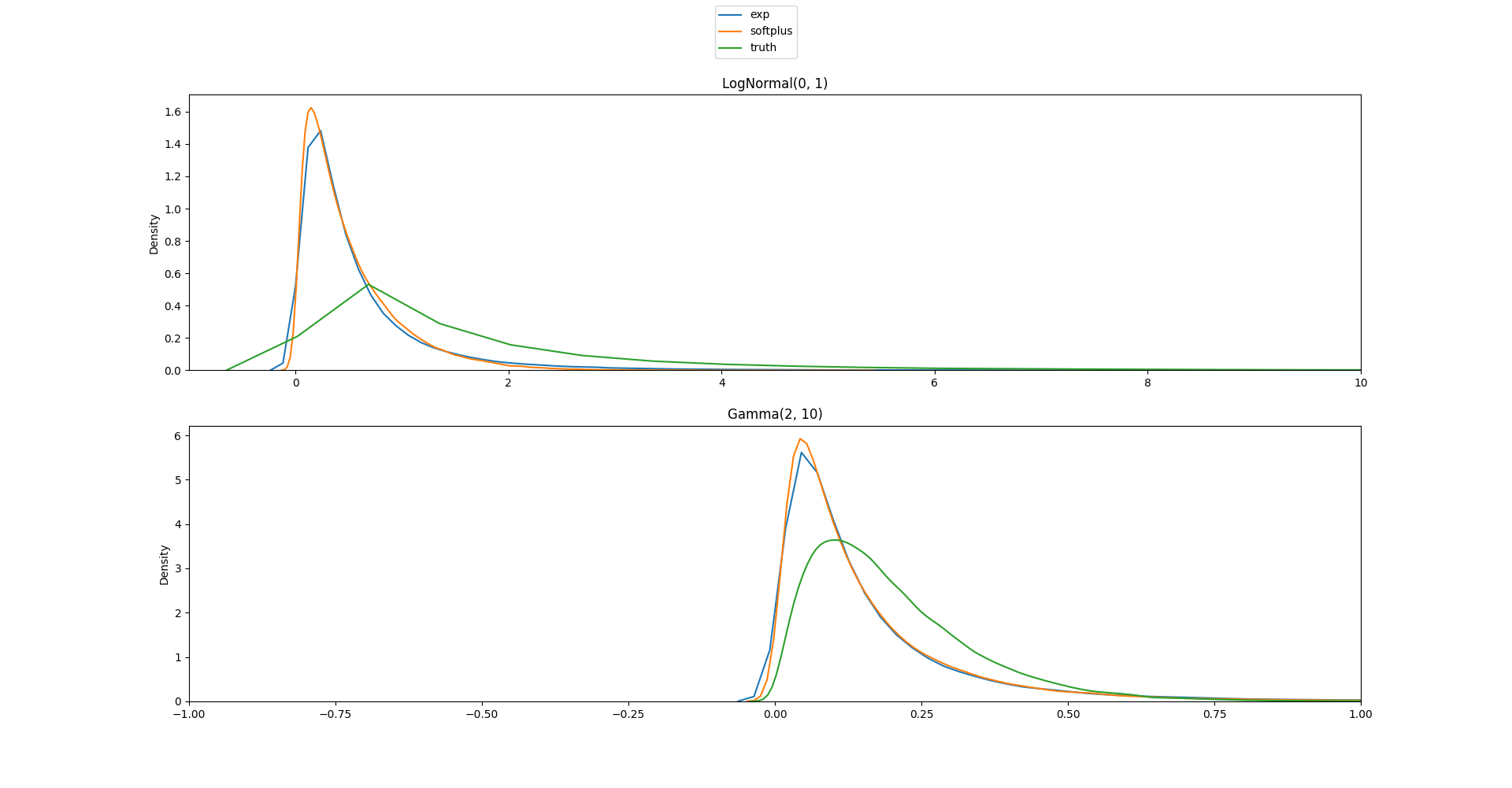
@ColCarroll if at all interesting, I've spent a little more time (not as much as I would like) on this and added another feature that I hope is useful - the ability to turn on/off the jacobian adjustment as described a little in the stan manual.

I've also added further testing of the covariance matrix as you suggested.

I'm not sure in what cases you'd want to turn on/off the jacobian adjustment, in stan it is always off, but in the first example I've tried I think I'd rather have it on? Here is the code and plots:

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

import tensorflow_probability as tfp

tfd = tfp.distributions
tfb = tfp.bijectors
tfde = tfp.experimental.distributions

import laplace_approximation as tfde

ADD_LOG_DET_JACOBIAN = True

a = tfd.LogNormal(loc=np.array(0.), scale=1.)
b = tfd.Gamma(concentration=np.array(2.), rate=10.)

joint_dist = tfd.JointDistributionSequential([a, b])

initial_values = [np.linspace(0.01, 5., 10)] * 2

e_approx = tfde.laplace_approximation(
    joint_dist,
    bijectors=[tfb.Exp()] * 2,
    initial_values=initial_values,
    add_log_det_jacobian=ADD_LOG_DET_JACOBIAN)

s_approx = tfde.laplace_approximation(
    joint_dist,
    bijectors=[tfb.Softplus()] * 2,
    initial_values=initial_values,
    add_log_det_jacobian=ADD_LOG_DET_JACOBIAN)

num_samples = 100_000
e_samples = e_approx.sample(num_samples)
s_samples = s_approx.sample(num_samples)
true_samples = joint_dist.sample(num_samples)

all_samples = [e_samples, s_samples, true_samples]
labels = ["exp", "softplus", "truth"]

fig, axs = plt.subplots(2, 1)

axs[0].set_title("LogNormal(0, 1)")
axs[0].set_xlim(-1, 10)

axs[1].set_title("Gamma(2, 10)")
axs[1].set_xlim(-1, 1)

for s, l in zip(all_samples, labels):
  sns.kdeplot(s[0].numpy(), label=l, ax=axs[0])
  sns.kdeplot(s[1].numpy(), label=l, ax=axs[1])

handles, labels = axs[1].get_legend_handles_labels()
fig.legend(handles, labels, loc="upper center")
fig.show()

with adjustment:

without the adjustment:

[jeffpollock9]

Hi, is there any appetite to get this finished off? If so I could devote some time to it. Thanks!