2D Burgers Equation

[engsbk]

Hello @levimcclenny and thanks for recommending this library!

I have modified the 1D burger example to be in 2D, but I did not get good comparison results. Any suggestions?

import math
import scipy.io
import tensordiffeq as tdq
from tensordiffeq.boundaries import *
from tensordiffeq.models import CollocationSolverND

Domain = DomainND(["x", "y", "t"], time_var='t')

Domain.add("x", [-1.0, 1.0], 256)
Domain.add("y", [-1.0, 1.0], 256)
Domain.add("t", [0.0, 1.0], 100)

N_f = 10000
Domain.generate_collocation_points(N_f)


def func_ic(x,y):
    p =2
    q =1
    return np.sin (p * math.pi * x) * np.sin(q * math.pi * y)
    

init = IC(Domain, [func_ic], var=[['x','y']])
upper_x = dirichletBC(Domain, val=0.0, var='x', target="upper")
lower_x = dirichletBC(Domain, val=0.0, var='x', target="lower")
upper_y = dirichletBC(Domain, val=0.0, var='y', target="upper")
lower_y = dirichletBC(Domain, val=0.0, var='y', target="lower")

BCs = [init, upper_x, lower_x, upper_y, lower_y]


def f_model(u_model, x, y, t):
    u = u_model(tf.concat([x, y, t], 1))
    u_x = tf.gradients(u, x)
    u_xx = tf.gradients(u_x, x)
    u_y = tf.gradients(u, y)
    u_yy = tf.gradients(u_y, y)
    u_t = tf.gradients(u, t)
    f_u = u_t + u * (u_x + u_y) - (0.01 / tf.constant(math.pi)) * (u_xx+u_yy)
    return f_u


layer_sizes = [3, 20, 20, 20, 20, 20, 20, 20, 20, 1]

model = CollocationSolverND()
model.compile(layer_sizes, f_model, Domain, BCs)

# to reproduce results from Raissi and the SA-PINNs paper, train for 10k newton and 10k adam
model.fit(tf_iter=10000, newton_iter=10000)

model.save("burger2D_Training_Model")
#model.load("burger2D_Training_Model")

#######################################################
#################### PLOTTING #########################
#######################################################

data = np.load('py-pde_2D_burger_data.npz')

Exact = data['u_output']
Exact_u = np.real(Exact)

x = Domain.domaindict[0]['xlinspace']
y = Domain.domaindict[1]['ylinspace']
t = Domain.domaindict[2]["tlinspace"]

X, Y, T = np.meshgrid(x, y, t)

X_star = np.hstack((X.flatten()[:, None], Y.flatten()[:, None], T.flatten()[:, None]))
u_star = Exact_u.T.flatten()[:, None]

u_pred, f_u_pred = model.predict(X_star)

error_u = tdq.helpers.find_L2_error(u_pred, u_star)
print('Error u: %e' % (error_u))

lb = np.array([-1.0, -1.0, 0.0])
ub = np.array([1.0, 1.0, 1])

tdq.plotting.plot_solution_domain2D(model, [x, y, t], ub=ub, lb=lb, Exact_u=Exact_u.T)

[levimcclenny]

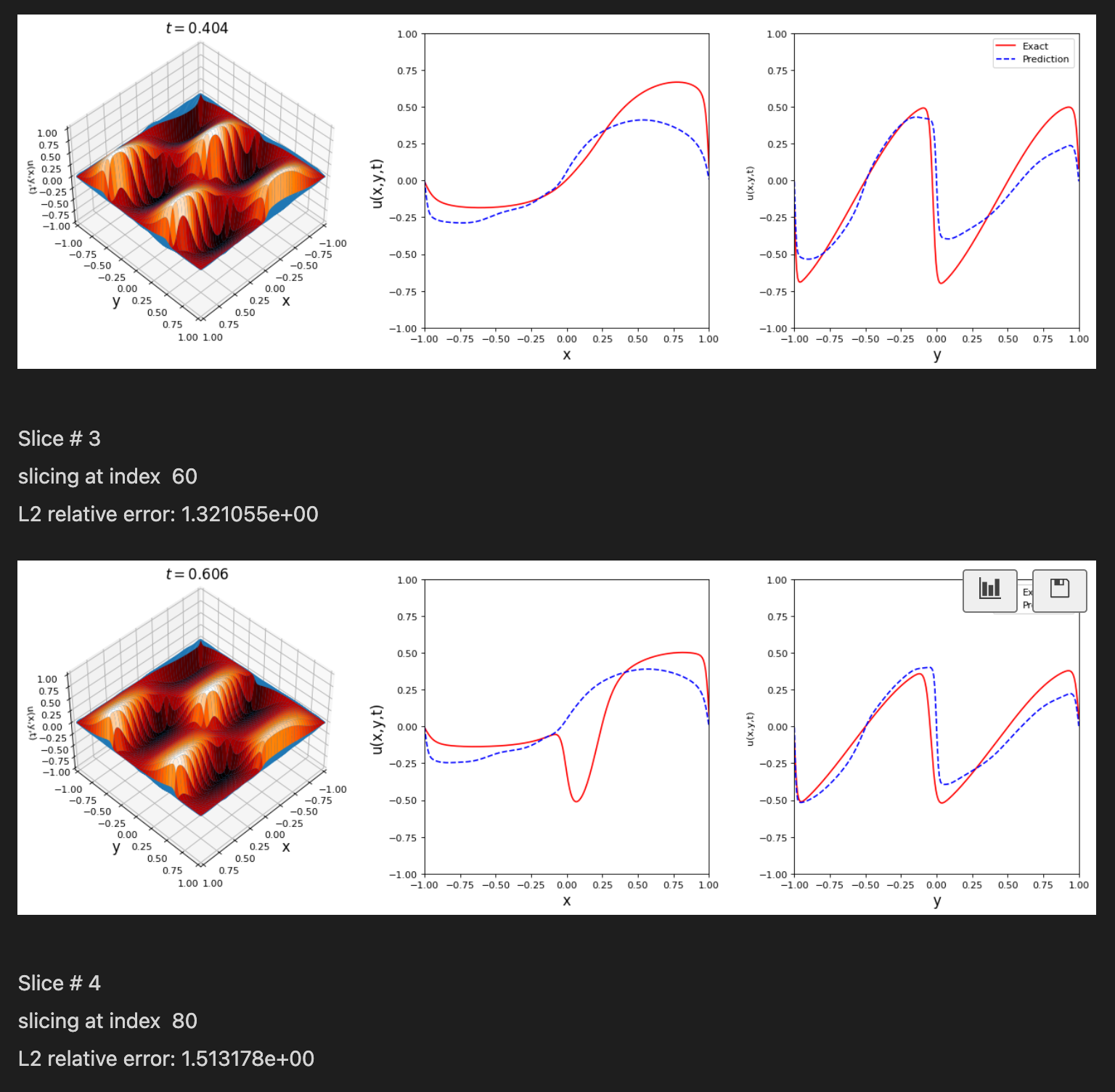
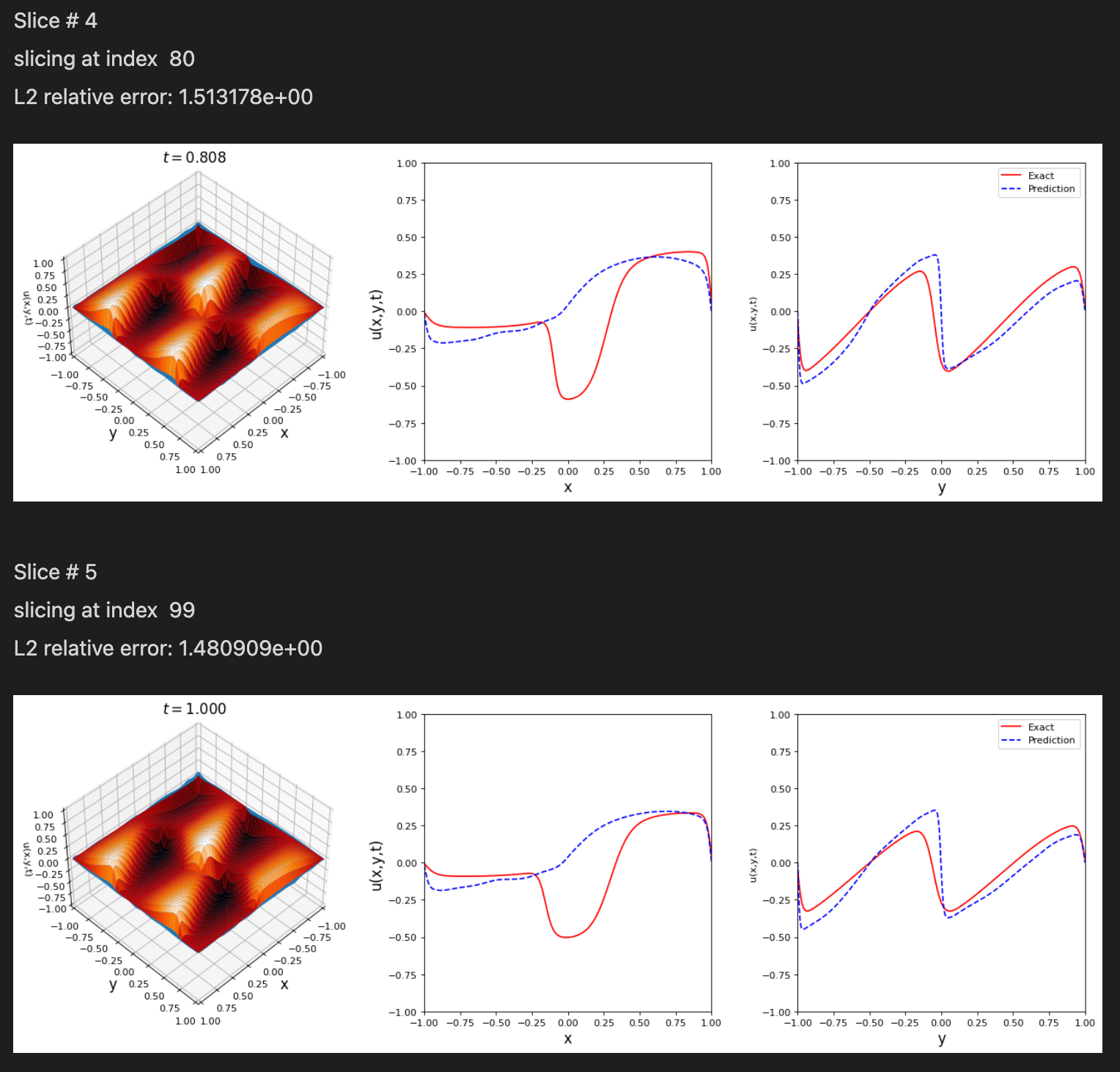
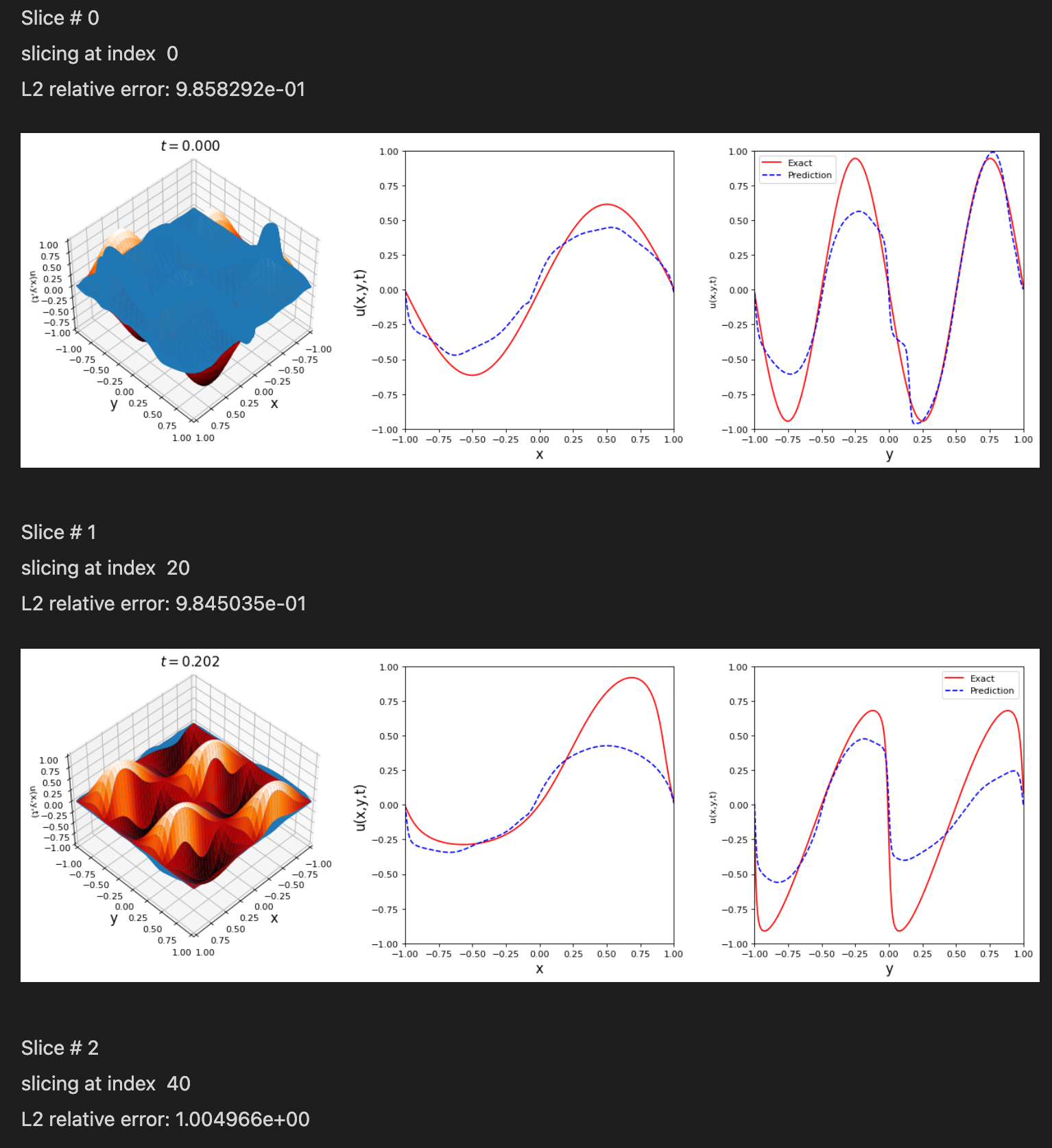
@engsbk I may try training for a little longer and adding the SA weighting scheme. 10k isn't too long of a training horizon, especially for a 2D problem. I would bump more Adam iterations and see where that takes you.

[levimcclenny]

@engsbk Did you train this one for longer? I really think that with more training iterations you'll get pretty good results here.

[engsbk]

Yes, I increased Adam epochs to 40,000. The results got better only on the first slice of time.

I was also trying to apply SA here, but when turning isAdaptive to true and using

dict_adaptive = {"residual": [True],
                 "BCs": [True, False, False, False, False]}
init_weights = {"residual": [tf.random.uniform([N_f, 1])],
                "BCs": [100 * tf.random.uniform([1,1,1,1,1]) , None]}

The loss in Adam training kept increasing which eventually showed loss = nan and I could not plot. Any ideas?