Support for Cancel

[Ali-Mohamed0]

I am currently working on circuit simulator, and i'am surprised by the great performance of symengine, especially lisolve function. the problem is the output of lisolve function is huge fraction, I want to simplify it to extract some data from it. I noticed that simplify function is not implemented in c++ yet, actually I only need Cancel algorithm from it.

Is this already implemented and I simply did not look in the right place? Are there any plans to support Cancel in the near future? Thanks a lot

[isuruf]

Can you give some examples of cancel that you would like to see?

[Ali-Mohamed0]

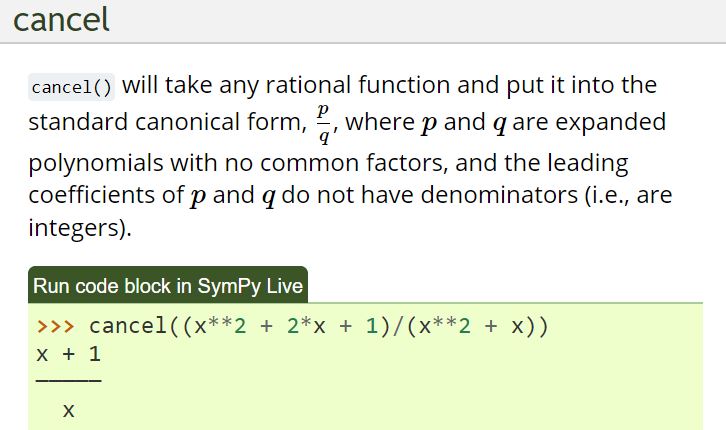
I tried sympy cancel function and it did the job well but very slow. it simplify the fraction into polynomial in numerator and polynomial in denominator. There are two examples in the attached pictures, one from sympy and the other from my work.

Thanks a lot.

[isuruf]

Here's something you can do in symengine,

In [23]: from symengine import *                                                                                                                                      

In [24]: var("V1, R1, C1 s")                                                                                                                                          
Out[24]: (V1, R1, C1, s)

In [25]: H = -V1/(R1**2 *(-((s*C1+R1**-1)/R1 - R1**-2)-R1**-2))                                                                                                       

In [26]: H                                                                                                                                                            
Out[26]: -V1/(R1**2*(-((s*C1 + R1**(-1))/R1 - R1**(-2)) - R1**(-2)))

In [27]: a, b = H.as_numer_denom()                                                                                                                                    

In [28]: a/b                                                                                                                                                          
Out[28]: -V1/(-1 - s*R1*C1)

Is this sufficient?

[Ali-Mohamed0]

I tried this before but unfortunately it was exponentially slow as circuit grow. linsolve outputs increase exponentially so as_numer_denom() become slow.

[isuruf]

@Ali-Mohamed0, so it does give you the output you need, but it's just slow. Is that correct?

[Ali-Mohamed0]

unfortunately No, in small expressions it do simplification but it doesn't simplify as cancel in large ones.

[isuruf]

Does something like below work?

In [29]: a, b = H.as_numer_denom()                                                                                                                                    

In [30]: a.expand()/b.expand()                                                                                                                                        
Out[30]: -V1/(-1 - s*R1*C1)

[Ali-Mohamed0]

Unfortunately no, and also the problem is as_numer_denom() is slow as expression grows up.

[isuruf]

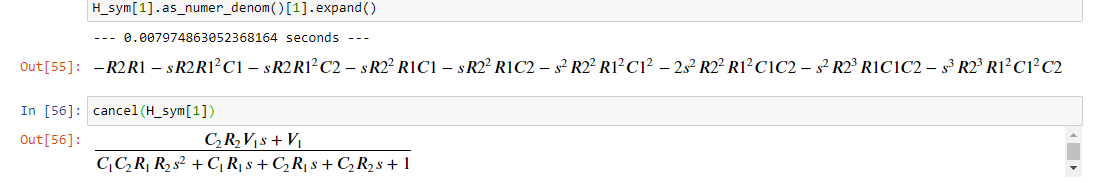
@Ali-Mohamed0, can you post the expression H_sym[1]?

[Ali-Mohamed0]

expression is output from solving the circuit. This is it as string.

-V1*(s*C2 + R2 ** (-1))*((s*C1 + R1 ** (-1) + R2**(-1))/R1 - R1** (-2))/(R1*(-1/(R2 ** 2*R1 ** 2) + R1 ** 2*(-1/(R2 ** 2*R1 ** 2) + (s*C2 + R2**(-1))*((s*C1 + R1 ** (-1) + R2**(-1))/R1 - R1**(-2))/R1)*(-((s*C1 + R1** (-1) + R2**(-1))/R1 - R1**(-2)) - R1** (-2))))

[Ali-Mohamed0]

I found something weird, when i try to use as_numer_denom() in symengine i found that it is slower 5 times than sympy. This is a that used in the expression. a = -(-1 + (2 + s)*(1 + s))/(-1 + ((1 + s)** 2*(-1 + (2 + s)*(1 + s)) - (1 + s)** 2)*(-1 + (-1 - (1 + s))*(-1 + (2 + s)*(1 + s)))/(1 + s)** 2)

Thanks a lot for helping @isuruf