Numerical instability for small ky rho_ref in branch feature/Davies-linear-EM-terms

[rd1042]

Issue to track a numerical instability in the electromagnetic stella branch feature/Davies-linear-EM-terms (commit 47f9f536). Possibly related to issue #98 (which mostly concerns the master branch).

Some details of the test case I'm examining has the features:

• CBC, with zero gradients
• Zero-incoming parallel BC
• Kinetic ions + kinetic electrons
• implicit treatment of streaming + mirror terms
• ky=0.05 , dt=0.004, upwinding parameters uz=0.02, ut=0.02, uvpa=0.02
• apar=bpar=0 i.e. an electrostatic problem. The differences between this implementation and the master branch is (1) the formulation of the GKE (uses h rather than/as well as g as distribution function variable) and (2) a refactoring of the response matrix for streaming to avoid code duplication. Some features of the instability:
• Occurs at low ky
• Occurs for all timestep sizes tried (in the range 1E-4 - 1) for ky=0.05. The instability growth rate increases as the timestep decreases (NB this is the opposite to the trend observed in the master branch, issue #98 )
• It appears this can be stabilised by increasing u_z (to ~0.3) or u_t (to ~0.3), but this may introduce too much dissipation for physical modes.
• Instability does not occur for the same input file using master branch (commit dcc6aa42). This becomes unstable when dt is increased (0.004 to e.g. dt=0.4), (consistent with #98 )
• Insensitive to whether the mirror term is implicit/explicit
• Making the streaming term explicit gives rise to an instability, but this looks a bit different (stabilised at sufficiently low dt). So I think there are 2 long-wavelength instabilities, which manifest depending on how parallel streaming is implemented.

Example input file attached. I'll provide more information/diagnostics shortly. It looks to me like some problem with the streaming algorithm. (Although there isn't an instability for the unsheared slab geometry with periodic BCs).

input.in.txt

[rd1042]

This appears to be related to how the centering is performed in the term (Z/T e^(-v^2) <Delta chi>) in the streaming scheme. The current scheme calculates this source term as: source_term = Z/T ( e^(-v^2) )_{centered_midpoint} * (<Delta chi>)_{centered}

This is O(dz^2) centered without z upwinding (i.e. u_z=0), but it "mixes" ( e^(-v^2) ) and (<Delta chi>) between adjacent gridpoints. An alternative is: source_term = Z/T ( e^(-v^2) * <Delta chi>)_{centered}

which is also O(dz^2) centered without z upwinding, but doesn't "mix" terms from adjacent gridpoints. This alternative approach is implemented in branch bugfix/Davies-linear-EM-terms-maxwellian-centering-streaming . With the same input file as above, this branch is stable. Some next steps/questions are:

• Is this approach stable for all ky/dt combinations?
• Can it be explained why the first approach is unstable?
• Is the same occurring in the master branch?

[rd1042]

Just an update that, with branch bugfix/Davies-linear-EM-terms-maxwellian-centering-streaming, numerical instability occurs if ky is reduced to e.g. 0.01. The numerical instability gets worse as the timestep increases, which is the opposite behaviour to the original instability, but the same behaviour as the master branch.

[mabarnes]

so should we interpret this as meaning that with the slight tweak to the centering in the EM implementation, the code behaves in the same way as the master branch? E.g., an electrostatic simulation with the delta phi and h formulations gives the same behaviour as master branch?

[rd1042]

Not quite - running the same input files for both simulations, the (delta phi and h) approach is more instability-prone (i.e. for a given ky, instability occurs if the timestep exceeds a partiuclar dt_max, and dt_max is smaller for the (delta phi and h) approach).

[rd1042]

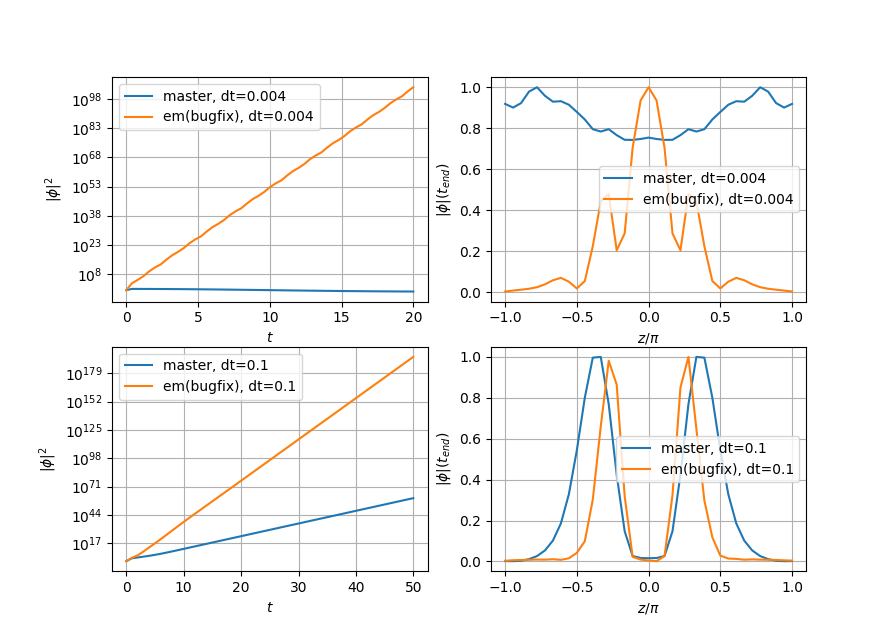
Attached are mode structures for master & em_stella (the latter with the bugfix) showing instabilities for different dt with ky=0.01. master is stable for dt=0.004 (and 0.04, but not shown) but becomes unstable for dt=0.1. The (delta phi and h) approach is unstable for dt=0.004. The mode structures are smooth in z, but seems to change between dt=0.004 and dt=0.1 for the em branch.