falcon-public
 falcon-public copied to clipboard
falcon-public copied to clipboard
Batch Normalization protocol does not match code implementation.
Hey, snwagh. I have been reading your paper of Falcon and found this repo. And I am interested in how you perform the computation of Batch Normalization.
I have the following two questions:
-
the implementation of BN seems to be just a single division
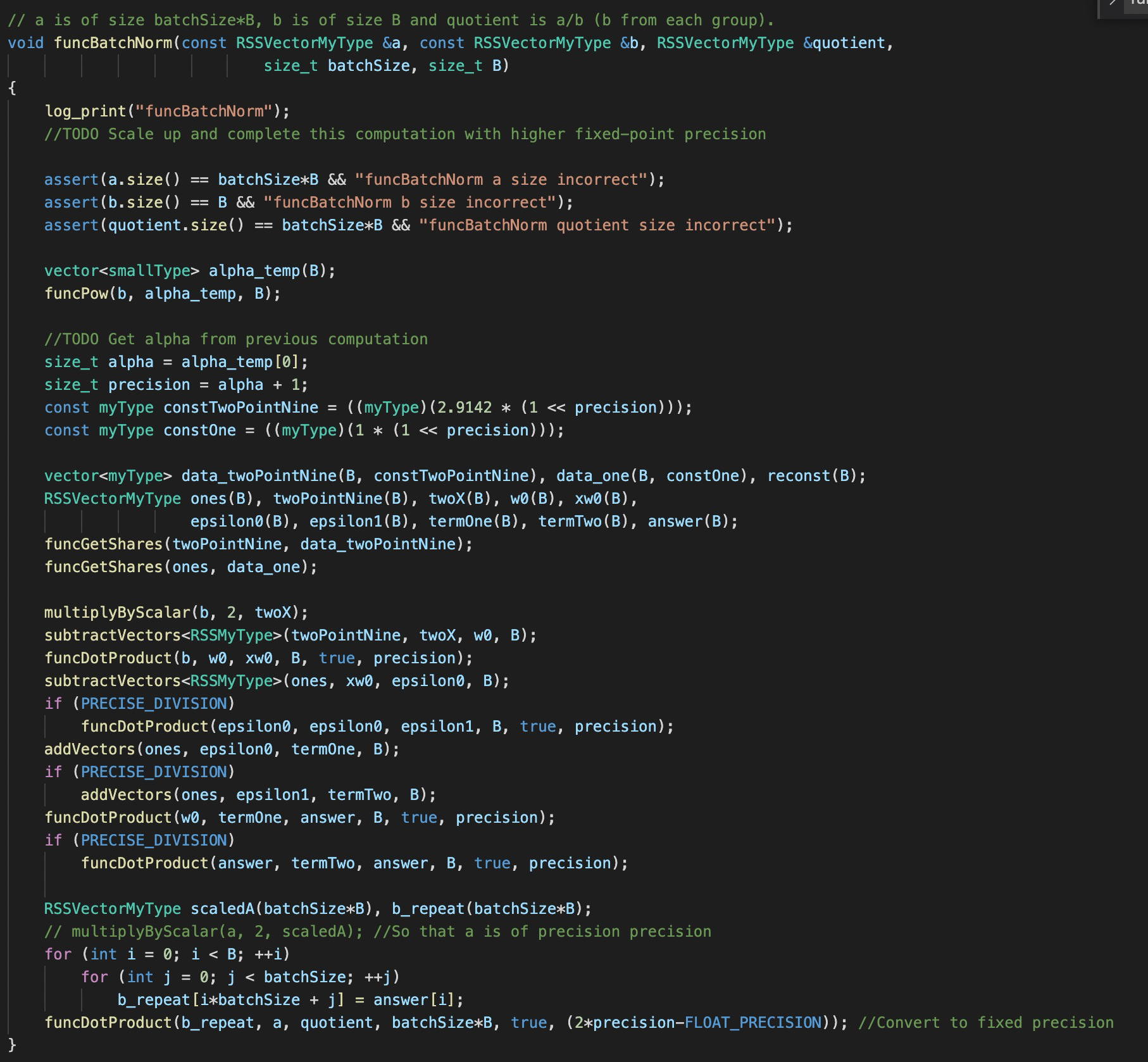
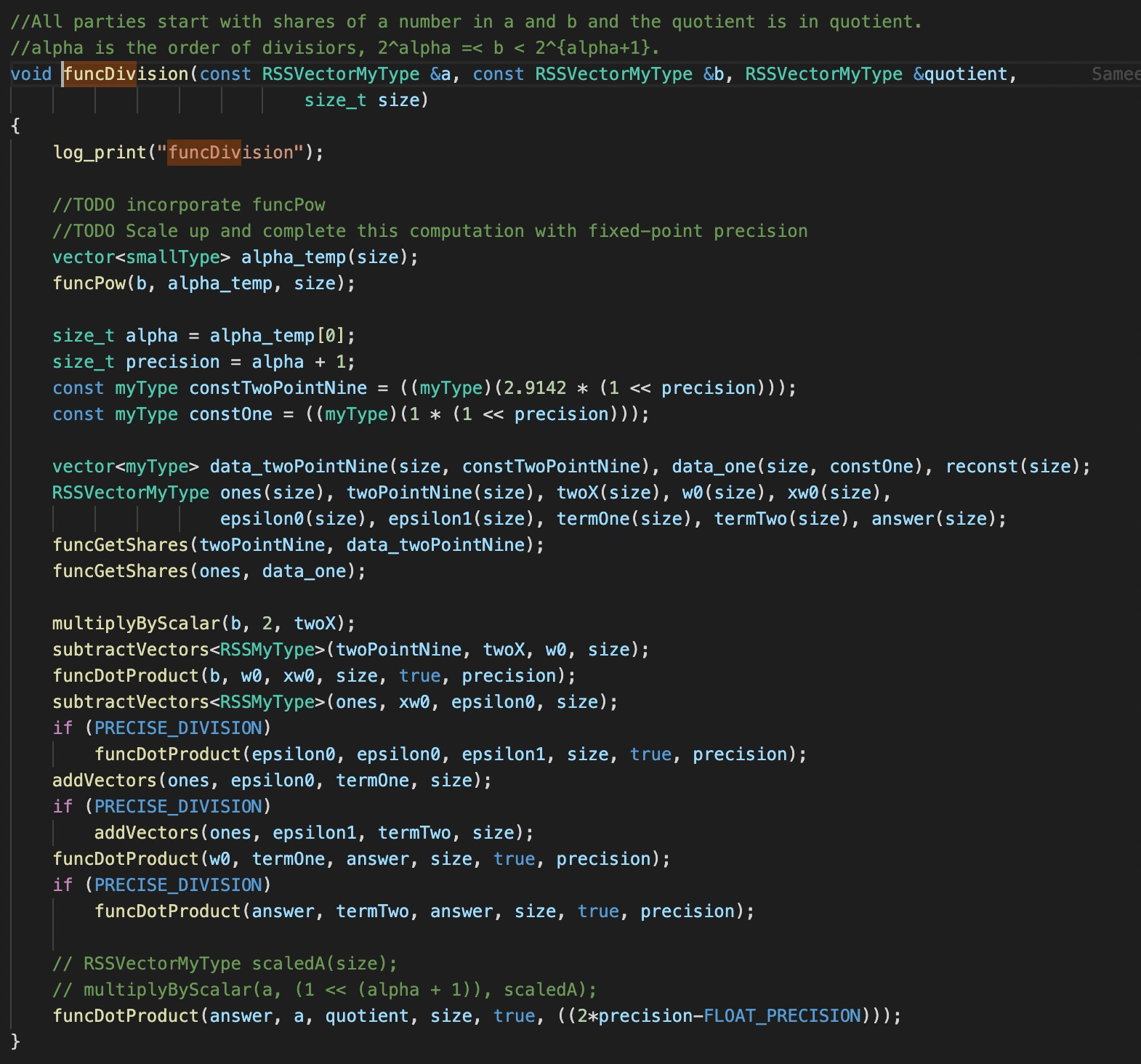
-
the protocol of
Powseems to reveal the information of the exponent, i.e., \alpha -
the BIT_SIZE in your paper is 32, which seems to be too small. How you guarantee the accuracy or say precision? IS the BN actually essential to your ML training and inference?
@llCurious I've added responses in order for your questions below:
- Right, the
Powfunction needs to be vectorized. Take a look at this git issue for more details. The division protocol also needs to be modified accordingly. The function correctly reports the run-time but effectively computes only the first component correctly. - The
Powdoes indeed reveal information of the exponent \alpha and it is by design (see Fig. 8 here). This considerably simplifies the computation and the leakage is well quantified. However, the broader implications of revealing this value (such as can an adversary launch an attack using that information) is not studied in the paper. - A
BIT_SIZEof 32 is sufficient for inference and the code to reproduce this is given in thefiles/preload/. End-to-end training in MPC was not performed (given the prohibitive time and parameter tuning) though I suspect you're right, it would either require a larger bit-width or adaptive setting of the fixed-point precision.
Thank you for you responses. Do you mean the division protocol currently can only handle the case where the exponent of the divisor b is the same? Or say, if the divisors in the vector have different exponents, then the current division protocol fails?
BTW, you seem to miss my question about the BN protocol. You mention that a larger bit-width or adaptive setting of the fixed-point precision. can be helpful in end-to-end training, do you mean to employ BN to tackle this problem?
Yes, that is correct. Either all the exponents have to be the same or the protocol doesn't really guarantee any correctness.
About your BN question, like I said, end-to-end training in MPC was not studied (still many open challenges for that) so it is hard to make a comment empirically on the use of BN for training. However, the use of BN is known from ML literature (plaintext) and the idea is that the benefits of BN (improving convergence/stability) will translate into secure computation too. Does this answer your question? If you're asking if BN will help train a network in the current code base then I'll say no, though it is an issue, it is not the only issue that is preventing training.
OK,i got it. Sry for the late reply~
-
I also notice that you in the Paper Section 5.6, you present the elemental data for the training performance with (or without) BN. I am a little bit confused that how the accuracy is obtained? It seems to be that this is end-to-end secure training?
-
In addition, i wonder how the comparison to prior works is conducted. Do you carry out the experiments of the prior works using 32-bit (which is identical to your setting) or the setting in their papers (like 64-bit in ABY3)?
Really thanks for your patient answers!!!!
- The numbers are for end-to-end training but unfortunately for plaintext.
- I think the numbers are identical (the fastest way to verify would be to run the Falcon code).