optimizing performance

[schlegelp]

Hi @Vannghia69. I just now had a chance to test your new implementation of the dendrogram optimization on a more realistic and larger dataset: depending on the size and the "alignability" (i.e. how easy it is to disentangle) of the two dendrograms, it becomes a prohibitively slow procedure.

For example, I had two dendrograms with just 14 leafs where I stopped the optimization after 10 minutes because it didn't look like it was going to converge anytime soon. With cdd30220baf49d46c6a2c0204af0bdf690c892e7 I made a couple changes such as using leave_list instead of dendrogram(..., no_plot=True) and avoid re-calculations of leaf order wherever possible.

However, the biggest issue still was that there were too many nested loops and that the number of linkage variants to test increased exponential (2, 4, 8, 16, 32, ...) with every li_MID step. Bottom line: we have to cut down on the number of nested loops somehow. I hope I read your code correctly but my understanding is that your implementation broadly did this (pseudo code):

for li_MID in range(number of hinges) (first loop):
   get all possible variations of rotating around the top li_MID hinges
   for every variant of the left dendrogram (second loop):
      for every variant of the right dendrogram (third loop):
         coarse refinement by testing all possible rotations from the bottom to li_MID (this contains multiple nested loops)
         fine refinement by rotating only the leaves (also loops)
         test entanglement of refined version and keep if better than what we've seen so far
   if entanglement has not improved twice break loop

I was wondering if it was sufficient only do a refinement at the very end, outside the main loop. Like this:

for li_MID in range(number of hinges) (first loop):
   get all possible variations of rotating around the top li_MID hinges
   for every variant of the left dendrogram (second loop):
      for every variant of the right dendrogram (third loop):
         test entanglement and keep if better than what we've seen so far
   if entanglement has not improved twice break loop
coarse refinement of the best linkage from the bottom to li_MID 
fine refinement by rotating only the leaves

Thoughts?

[Vannghia69]

Hi Phillipp,

First of all, I appreciate that you spent time testing my code and indicating the drawback of it.

Second of all, I agree with you that the method contains lots of nested loops, which makes the running time longer and unpredictable. With the problem I am working with, it takes approximately 10 to 20 mins to run the program. I am definitely considering your suggestion to decrease the number of loops. In the meantime, could you run the code again using your real data and please be patient? It is worth to wait a bit longer I reckon.

One thing we both know is that when Li_MID is increased by 1, the number of linkage variants to test is double and some of them might be examined in the previous "Li-MID loop". I used to choose ONLY ONE value of Li-MID (for example 3, not an interval from 1 to Li-MID) to shorten the running time. However, this number must be different in distinct data to make sure that the result is the real minimum. Therefore, I need it to run from 1 to "some point", until the result is repeated 2 times or 3 times. I am trying to solve this problem.

I will keep you updated with new improvements.

Best regards, Nghia

---

From: Philipp Schlegel [email protected] Sent: Thursday, 21 January 2021 17:01 To: schlegelp/tanglegram [email protected] Cc: Van Nghia Nguyen [email protected]; Mention [email protected] Subject: [schlegelp/tanglegram] optimizing performance (#9)

Hi @Vannghia69https://github.com/Vannghia69. I just now had a chance to test your new implementation of the dendrogram optimization on a more realistic and larger dataset: depending on the size and the "alignability" (i.e. how easy it is to disentangle) of the two dendrograms, it becomes a prohibitively slow procedure.

For example, I had two dendrograms with 14 leafs where I stopped the optimization after 10 minutes because it didn't look like it was going to converge anytime soon. With cdd3022https://github.com/schlegelp/tanglegram/commit/cdd30220baf49d46c6a2c0204af0bdf690c892e7 I made a couple changes such as using leave_list instead of dendrogram(..., no_plot=True) and avoid re-calculations of leaf order wherever possible.

However, the biggest issue still was that there were too many nested loops and that the number of linkage variants to test increased exponential (2, 4, 8, 16, 32, ...) with every li_MID step. Bottom line: we have to cut down on the number of nested loops somehow. I hope I read your code correctly but my understanding is that your implementation broadly did this (pseudo code):

for li_MID in range(number of hinges) (first loop): get all possible variations of rotating around the top li_MID hinges for variant of the left dendrogram (second loop): for variant of the right dendrogram (third loop): coarse refinement by testing all possible rotations from the bottom to li_MID (this is also a loop) fine refinement by rotating only the leaves (also a loop) test entanglement of refined version and keep if better than what we've seen so far if entanglement has not improved twice break loop

I was wondering if it was sufficient only do a refinement at the very end, outside the main loop. Like this:

for li_MID in range(number of hinges) (first loop): get all possible variations of rotating around the top li_MID hinges for variant of the left dendrogram (second loop): for variant of the right dendrogram (third loop): test entanglement and keep if better than what we've seen so far if entanglement has not improved twice break loop coarse refinement of the best linkage from the bottom to li_MID fine refinement by rotating only the leaves

Thoughts?

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHubhttps://github.com/schlegelp/tanglegram/issues/9, or unsubscribehttps://github.com/notifications/unsubscribe-auth/ASOPE3BMD6XBO4M77UD5LMDS3BFWXANCNFSM4WNDMMGQ.

[schlegelp]

Looking at the dendextend package for R, they only do alphanumerical label sorting in their tanglegram function to align the trees.

I imagine several minutes per run will be prohibitive for most users. At the moment I am leaning toward implementing multiple levels of sorting - something like None, "minimal" and "optimal" - with the highest level being your thorough implementation.

[Vannghia69]

Actually, in R, they have several methods such as step1side, step2side, ladderize, DenSer... I am comparing the results from R with my result.

[Vannghia69]

I have the reason not to put the coarse and fine refinements outside of the outer loop.

Let say you are finding a pair of dendrograms, which has the smallest entanglement among all possible pairs (step 1). Then from that pair, you apply the coarse and fine refinement and find the minimum entanglement (step 2). Unfortunately, the result at the end of step 2 is still the local minimum. The global minimum can be "hidden" in the pair of dendrograms with a large entanglement. Finding a good pair does not mean that the global minimum can be found from it.

I did alter the code as you suggested and the results are not the global minimum.

[schlegelp]

With 7c2ab07fffaae08fa89b347e729af1742a088764 I implemented a couple untangling methods from dendextend:

• new function untangle() that pools below untangling methods
• new untangling (sub)functions:
  • untangle_permutations(): this is your method
  • untangle_step_rotate_2side(): rotate around each knot/hinge in both dendrograms
  • untangle_step_rotate_1side(): rotate around each knot/hinge in one dendrograms
  • untangle_random_search(): randomly shuffled dendrograms R times
• dropped _optimizing_order() in favor of the above
• implemented a distance norm L for entanglement

For your method, I made some I hope useful changes:

• use generators for the permutations
• stop condition is now a target entanglement -> this is not ideal but I didn't get how your old stop condition worked - maybe you have a better idea?
• add a progress bar
• some other small improvements

Let me know what you think.

[Vannghia69]

Hi,

Thank you for your updates! The code looks much better with these improvements.

With regard to the stop condition, it is a good idea to terminate the program when we reach the entanglement of 0. But we rarely get it with large and complicated data. The target is to find the smallest entanglement which is unknown. Hence, my convergence condition is the repeat of entanglement in two consecutive values of li_MID when we are expanding the permutations. I have been thinking a lot about how to improve the permutation but it seems to be inevitable to do this way. I believe rotating the first hinges at the top of dendograms plays a very important role in not skipping the case which we can get the global minimum from. Methods in R fail in finding the global minimum because it just focuses on decreasing the entanglement value but in fact, we might need to increase that value to get a much smaller value later on.

I have just compared the efficiency of some untangle methods (in terms of the ability to find the smallest entanglement, not the computational time). Here I run the random method with 1 000 000 iterations, which takes around 15 mins. Then I picked up 50 values (each every 200 values) to plot with other methods. The entanglement values are not normalized yet.

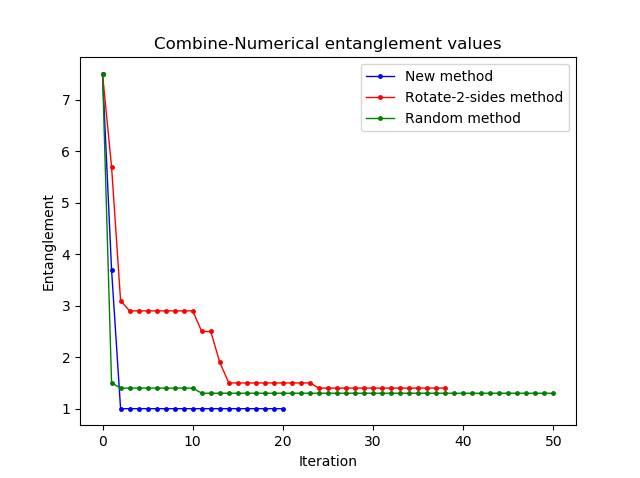
What's your opinion?

[schlegelp]

I think there is certainly a place for the permutation method. I would probably implement a few optional stop conditions (time, number of runs, no improvement in consecutive runs) for it so the user can pick their own poison.

A quick Google search dug up a few research articles on the tanglegram problem but I don't have the time - and quite frankly not the background - to dig into those. Just in case you feel like having a jab, this conferences paper on "Generalized Binary Tanglegrams: Algorithms and Applications" seems relevant. They even say they implemented some stuff in Python but I couldn't find it off the bat and the paper is 12 years old by now.

As to your benchmark: good stuff! I suspect that depending on the conditions, the permutation method might be the fastest to get to the global minimum while random/2-side will be faster to get you close-ish to that minimum. Two comments:

First, it might be better to plot the time on the x-axis rather than iterations since (a) a single iterations don't take the same amount of time across methods and (b) later iterations in the permutation method are exponentially slower than earlier ones.

Second: what's the size of the tree there? From the entanglement, I suspect that your tree is relatively small and this figure might look very different with even just slightly larger trees. You could check by trying various different tree sizes and plotting tree size on the x-axis against entanglement after N mins or time to reduce entanglement below 0.1 (normalized) on the y-axis.

[Vannghia69]

I will have a look at the paper and also focus on how to plot more wisely. I used the trees which I showed you before. Thanks for your thoughts!

Get Outlook for Androidhttps://aka.ms/ghei36

---

From: Philipp Schlegel [email protected] Sent: Sunday, January 24, 2021 3:18:11 PM To: schlegelp/tanglegram [email protected] Cc: Van Nghia Nguyen [email protected]; Mention [email protected] Subject: Re: [schlegelp/tanglegram] optimizing performance (#9)

I think there is certainly a place for the permutation method. I would probably implement a few optional stop conditions (time, number of runs, no improvement in consecutive runs) for it so the user can pick their own poison.

A quick Google search dug up a few research articles on the tanglegram problem but I don't have the time - and quite frankly not the background - to dig into those. Just in case you feel like having a jab, thishttp://people.csail.mit.edu/mukul/BCEF_Tanglegrams09.pdf conferences paper on "Generalized Binary Tanglegrams: Algorithms and Applications" seems relevant. They even say they implemented some stuff in Python but I couldn't find it off the bat and the paper is 12 years old by now.

As to your benchmark: good stuff! I suspect that depending on the conditions, the permutation method might be the fastest to get to the global minimum while random/2-side will be faster to get you close-ish to that minimum. Two comments:

First, it might be better to plot the time on the x-axis rather than iterations since (a) a single iterations don't take the same amount of time across methods and (b) later iterations in the permutation method are exponentially slower than earlier ones.

Second: what's the size of the tree there? From the entanglement, I suspect that your tree is relatively small and this figure might look very different with even just slightly larger trees. You could check by trying various different tree sizes and plotting tree size on the x-axis against entanglement after N mins or time to reduce entanglement below 0.1 (normalized) on the y-axis.

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHubhttps://github.com/schlegelp/tanglegram/issues/9#issuecomment-766355521, or unsubscribehttps://github.com/notifications/unsubscribe-auth/ASOPE3G2Z2IQ23WYV4AFTWLS3QT2HANCNFSM4WNDMMGQ.

[Vannghia69]

Two ways to decrease the running time and the size of permutations:

1. Each time we increase the Li_MID we just take care of the newly-rotated-tree combinations and skip the old ones. This declines half of the running time. I did apply this solution and it worked.

2. We skip the very first numbers of Li_MID and start with a specific value. This value depends on the size of the tree. For example, with a tree of size 20, Li_MID could be 4 (if the root is 1) so that it creates enough varients in permutation and could be able to find out the global minimum. This solution seems to be vague but it is worth to think of.

What do you think?

[schlegelp]

Good thoughts!

Unless I'm misunderstanding 1, this is already implemented - see this line: https://github.com/schlegelp/tanglegram/blob/2d2072baa62bfafae152aef0730f69c5de24a05c/tanglegram/tangle.py#L457

If 1 is implemented, then we don't need 2, right?

[Vannghia69]

You are not misunderstood. However, there is a problem with the get_all_linkage_gen generator which generates only new layouts of the tree. In fact, we need the old ones also in order to pair with the new layouts of the other tree (to get a new variant of the tanglegram). For example, in the first iteration, we rotate the root so we have layouts A, B (tree 1) and A', B' (tree 2). We have 4 variants AA', AB', BA', BB'. In the next iteration, we should have the following layouts: A, B, C, D (tree 1) and A', B', C', D' (tree 2). At this point, we are interested in the new variants AC', AD', BC', BD', CA', CB', CC', CD', DA', DB', DC', DD' and skip the old variants which are studied in the previous iteration. The generator above gives us only C, D (tree 1) and C', D' (tree 2). Therefore, you can see that it ignores some variants. We need to fix that, don't we?

[Vannghia69]

I did run the updated program using the generator for permutation and it did not return the results I expected.

[schlegelp]

get_all_linkage_gen () should be doing what you describe - i.e. return all possible combinations.

If you look at the code, you will notice that it always begins rotating at the top but does not actually start returning combinations until the defined start. Basically: all possible rotations from the top are performed but not necessarily returned.

Can you provide a minimal example of what you expect vs where you think the generator is not doing the correct thing?

[Vannghia69]

For example, we start with an original tree A (tree 1). When you rotate the first hinge which is the root does the generator return 2 layouts A and B or only B? I tested it and it returned B only. I expected that it gave me A and B.

[schlegelp]

A little example:

# The function without the leaf order/label stuff
def get_all_linkage_gen(linkage, stop, start=0):
    length = len(linkage)
    linkage = linkage.reshape(-1, length, 4)

    # Invert to/from
    start = length - 1 - start
    stop = length - 1 - stop

    i = length - 1
    while i > stop:
        # Use range because linkage will change in size as we edit it       
        for j in range(len(linkage)):
            # This is the new linkage matrix
            new = linkage[j].copy()
            new[i][0], new[i][1] = new[i][1], new[i][0]

            if i <= start:
                yield new

            linkage = np.append(linkage, new)
            linkage = linkage.reshape(-1, length, 4)
        i -= 1 

>>> import numpy as np
>>> # A mock linkage 
>>> Z = np.array([['a', 'b', None, None], ['c', 'd', None, None]])
>>> # Initialize generator
>>> gen = get_all_linkage_gen(Z, stop=2, start=0)
>>> # Get all combinations
>>> list(gen)
[array([['a', 'b', None, None],
        ['d', 'c', None, None]], dtype=object),
 array([['b', 'a', None, None],
        ['c', 'd', None, None]], dtype=object),
 array([['b', 'a', None, None],
        ['d', 'c', None, None]], dtype=object)]

>>> # Same thing but skip the first rotationn
>>> gen2 = get_all_linkage_gen(Z, stop=2, start=1)
>>> list(gen2)
[array([['b', 'a', None, None],
        ['c', 'd', None, None]], dtype=object),
 array([['b', 'a', None, None],
        ['d', 'c', None, None]], dtype=object)]

Looks alright to me but maybe there is an error in how that generator is invoked in untangle_permutations()?

[schlegelp]

Actually, comparing your original non-generator implementation I see now that the generator also ought to return the original configuration. Will fix that.

[Vannghia69]

I understand the example. The problem is how do you get all the possible combinations if you skip the old layouts.

[Vannghia69]

Yes. We will fix that :)

[schlegelp]

The problem is how do you get all the possible combinations if you skip the old layouts.

That's exactly my point: it does not skip the old layouts - it just does not return them so we don't have to do the whole bottom-up/refinement again.

[Vannghia69]

Yes. It does not return them. But we need them to pair with the new ones of the other tree.

[schlegelp]

Ah now we're getting somewhere.

[schlegelp]

But then I'm confused re your previous statement:

Each time we increase the Li_MID we just take care of the newly-rotated-tree combinations and skip the old ones. This declines half of the running time. I did apply this solution and it worked.

[Vannghia69]

I think that statement is not precise. The newly-rotated-tree combinations here refer to all combinations that are new compared to the previous iterations. They can include the newly-rotated trees and the old trees.

[Vannghia69]

One more thing is that it is necessary to execute the bottom_up function several times until no further improvement. It seems that you apply it only one time.

[Vannghia69]

Hi, I run your new program but it did not give me the smallest entanglements. I tried to test the functions bottom_up and refine. It seemed that the problem came from these functions. Will find out soon.

[Vannghia69]

Here is an example: I tested the function bottom_up with li_MID (stop) = root for the same linkages. The old bottom_up gave me a result of 0.21 (the first picture). The new bottom-up returned the result of 0.43 (the second picture). We can see how different the functions rotated the hinges.

[Vannghia69]

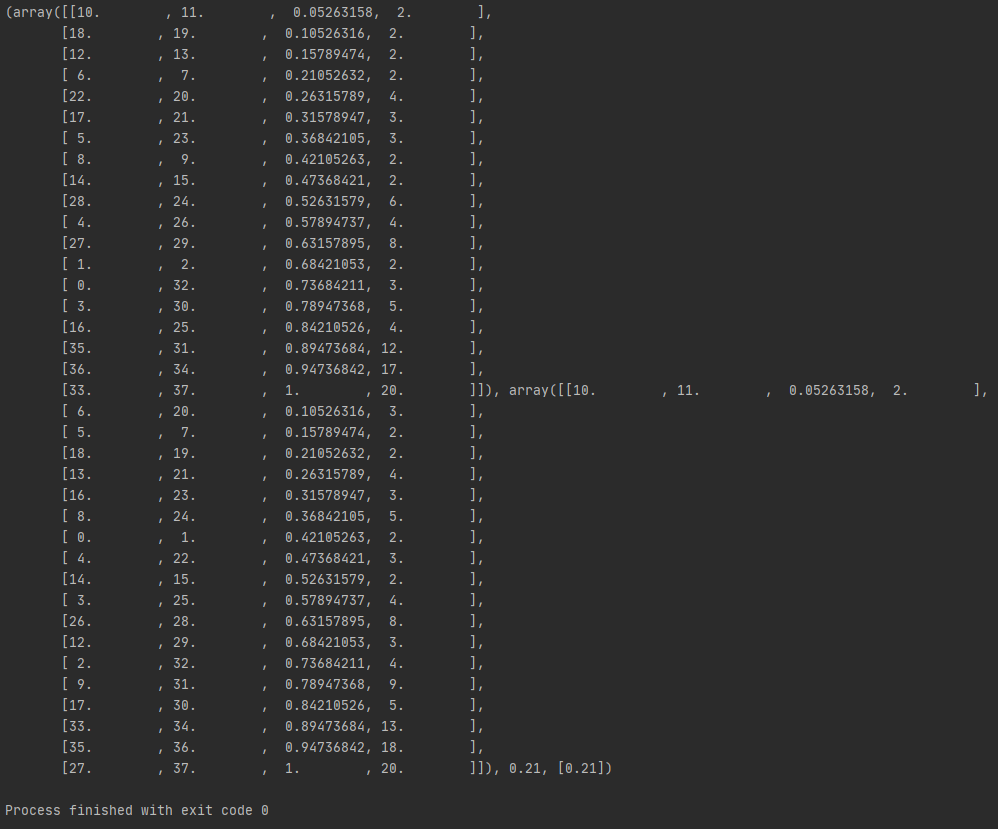
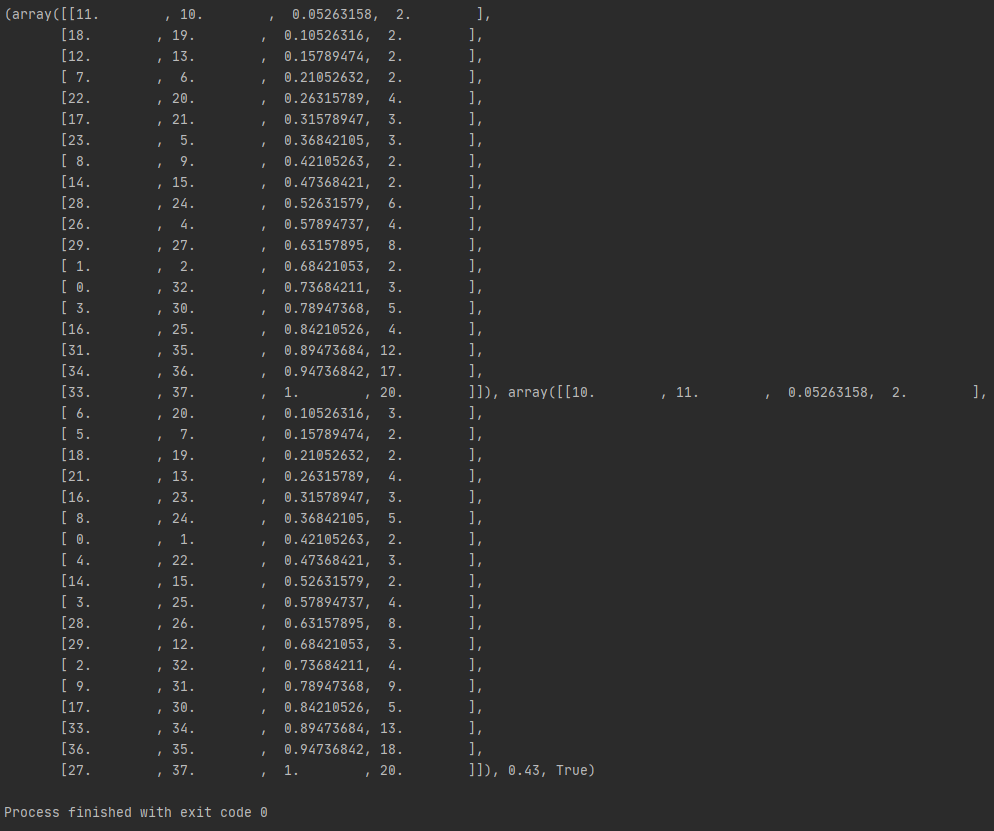
I suspect that the entanglement function gives us different results from the get_entanglement function (the old function). I rotated one hinge in a linkage I have and I calculated the entanglement with L=1. The entanglement function gave 0.66 (absolute entanglement 132). Whereas, the old function gave 0.67 (absolute entanglement 134). The worst entanglement was 200.