Rounding number of successes in the negative binomial distribution to the closest integer

[leoisl]

trafficstars

By default, pandora computes the log likelihood of minimizer kmers in a PRG to find the maximum likelihood path using a Negative Binomial distribution where the number of successes (negative_binomial_parameter_r) is the number of times a kmer was read incorrectly, and the probability of success (negative_binomial_parameter_p) is the probability of reading a kmer incorrectly:

https://github.com/rmcolq/pandora/blob/955e1c0c7bcd127361d66a74342a8ac19d651a2a/src/kmergraphwithcoverage.cpp#L95-L104

Like this we can compute the likelihood of a minimizer kmer given its coverage and this distribution.

There is a technical incompatibility with this approach and the simulations based on the Negative Binomial RNG required by the genotype confidence percentiler implementation (https://github.com/rmcolq/pandora/issues/216).

While the likelihoods of minimizer kmers are computed using boost::math::negative_binomial, which accepts a continuous negative_binomial_parameter_r values, the object used to compute random kmer coverages for the percentiler, boost::random::negative_binomial_distribution, do not. We need to transform the double value to an int, and thus we get these differences in the distribution (blue is the distribution used by pandora to compute likelihoods of minimizer kmers, and green are the simulated coverages for the GCP):

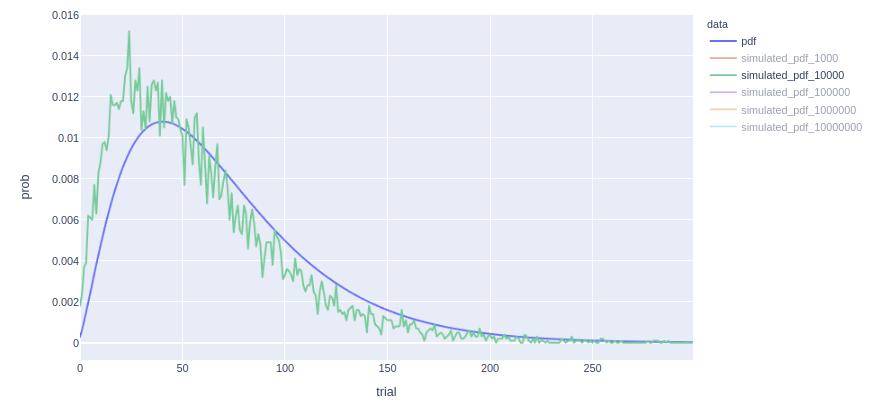
This was observed on real data, sample 063_STEC, where we have the following values for the Negative Binomial model parameters:

    double negative_binomial_parameter_r = 2.41921;
    double negative_binomial_parameter_p = 0.0335631;

In this case, the percentiler draws random values from a negative binomial distribution with negative_binomial_parameter_r = 2, instead of 2.41921, and thus the difference.

I don't think this is a problem with boost, as the function used by Minos to simulate coverages based on negative binomial also truncates this value to int: https://numpy.org/doc/1.16/reference/generated/numpy.random.negative_binomial.html

Therefore in order to enable the GCP to simulate values on the correct distribution, and for it to give us correct percentiles, I think we should round negative_binomial_parameter_r to the closest integer value... or maybe truncate?

[iqbal-lab]

The NB distribution is not defined for non integer params

One option is to use a continuous generalisation of the NB distribution. See Gordon Smyth's answer here: https://stats.stackexchange.com/questions/310676/continuous-generalization-of-the-negative-binomial-distribution

I'm confused how some boost functions do/not accept non-integer values.

Would like to talk through what is going on

[leoisl]

We are having issues with results on ONT data on the branch where we implemented GCP (https://github.com/leoisl/pandora/tree/GCP). ROC on ONT data shows that our precision and recall dropped significantly due to some changes in this branch. This rounding is the only thing I think that might be affecting results, and we might need to rollback the changes. GCP implementation should not affect results. https://github.com/rmcolq/pandora/issues/217 might also affect results, but this is actually a bug (we might need to adjust the min kmer covg threshold if this is the issue (maybe exp_depth_covg / 10 is not good for all samples)).

I pushed some commits with some changes in this branch. boost::math::negative_binomial, which is used to model the kmer coverage, keeps accepting a continuous negative_binomial_parameter_r value (as before, but this is still weird for me that it is a continuous value), while boost::random::negative_binomial_distribution, which is used to simulate kmer coverages for the percentiler, uses the closest int value. The percentiler will receive a distribution that is a bit different than the distribution of the kmer coverage model, e.g.:

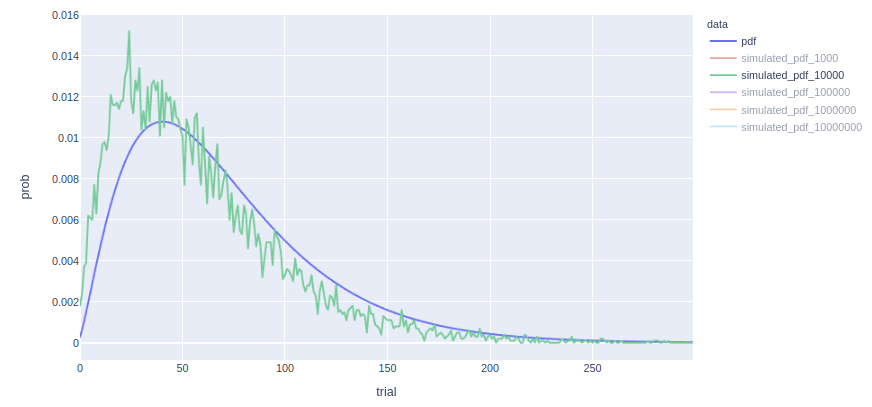
so we will endup with over or underestimated percentiles, but this is still better than affecting calls.

Pipeline is running, and will update on the new results.