Include proper feature engineering and pruning to create a reasonable cost function
A preliminary test indicates that using 1.6*log(ppm+1)+log(uncertainty_unit_cost) as the cost function works pretty well for feature engineering. This has a nice implication on runtime. As with proper feature engineering one can prune in an educated way. Note that the min costflow solver here is constantly below 0.1 seconds!
Features were motivated by this diagram:
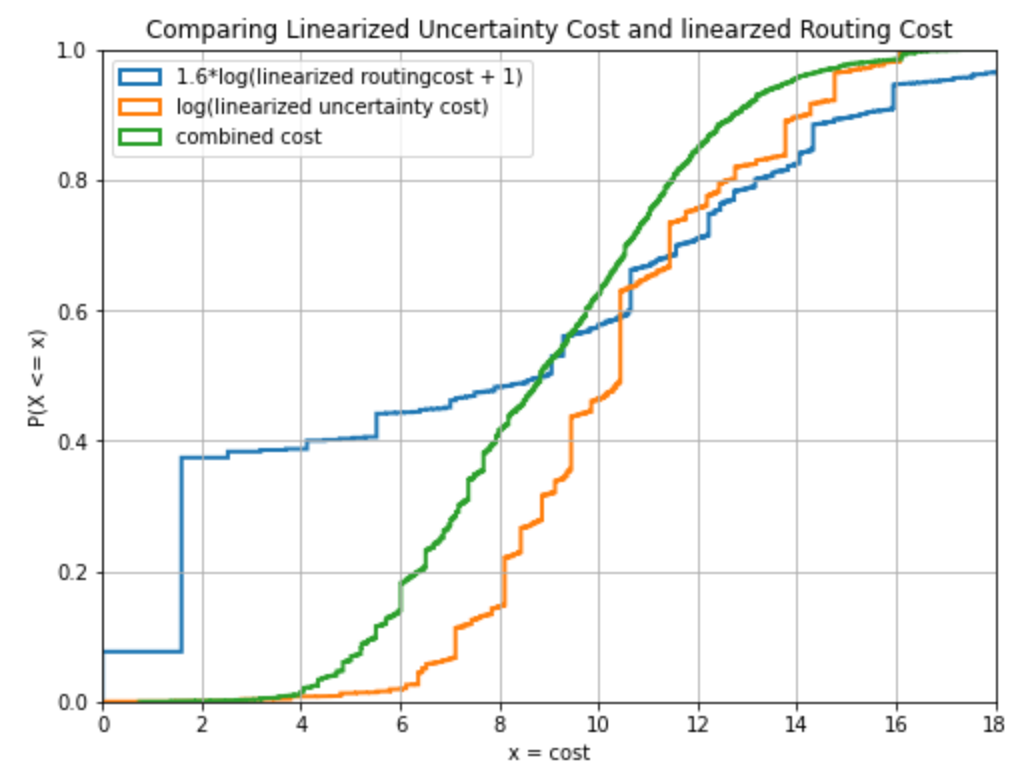
where a combined cost of 8 corresponds to pruning everything but the 20% cheapest channels (cheap as in low combined cost) as indicted by this addation to the prepare_min_cost_flow_solver indicates:
if self._prune_network:
neighbor = False
if channel.src ==src or channel.dest == dest:
neighbor = True
routing_cost = channel.linearized_integer_routing_unit_cost()
uncertainty_cost = channel.linearized_integer_uncertainty_unit_cost()
if neighbor == (False and 1.6*log(routing_cost+1) + log(uncertainty_cost))/2 > 8:
break
Here is a log of a run where the min cost flow problem is solved on the pruned network with the regular cost function (linearized_integer_uncertainty_cost + my*linearized_integer_routing_cost) and mu=1
Round number: 1
Try to deliver 29091333 satoshi:
Statistics about 29 candidate onions:
successful attempts:
--------------------
p = 78.46% amt: 192000 sats hops: 2 ppm: 1342
p = 52.80% amt: 1200000 sats hops: 2 ppm: 2572
p = 78.58% amt: 177822 sats hops: 2 ppm: 1415
p = 69.33% amt: 400000 sats hops: 2 ppm: 1382
p = 76.00% amt: 200000 sats hops: 2 ppm: 1382
p = 77.95% amt: 220000 sats hops: 3 ppm: 1439
p = 73.92% amt: 194200 sats hops: 3 ppm: 1362
p = 99.69% amt: 4329 sats hops: 3 ppm: 1757
p = 49.07% amt: 1214012 sats hops: 3 ppm: 1465
p = 27.37% amt: 2674502 sats hops: 3 ppm: 1537
p = 50.33% amt: 400000 sats hops: 4 ppm: 1562
p = 46.22% amt: 3000000 sats hops: 4 ppm: 1410
p = 38.17% amt: 145043 sats hops: 4 ppm: 1378
p = 26.31% amt: 648823 sats hops: 4 ppm: 1466
p = 20.79% amt: 1400000 sats hops: 5 ppm: 1375
p = 21.55% amt: 3200000 sats hops: 5 ppm: 1362
p = 18.59% amt: 1520569 sats hops: 5 ppm: 1352
p = 17.39% amt: 565988 sats hops: 5 ppm: 1451
p = 30.51% amt: 500000 sats hops: 5 ppm: 1344
failed attempts:
----------------
p = 64.00% amt: 1000000 sats hops: 2 ppm: 1360
p = 72.00% amt: 200000 sats hops: 2 ppm: 1357
p = 76.60% amt: 200000 sats hops: 3 ppm: 1548
p = 48.09% amt: 600000 sats hops: 3 ppm: 1548
p = 46.47% amt: 825478 sats hops: 3 ppm: 1486
p = 49.20% amt: 2453124 sats hops: 3 ppm: 1365
p = 35.01% amt: 2000000 sats hops: 3 ppm: 1567
p = 23.38% amt: 2000000 sats hops: 5 ppm: 1460
p = 10.11% amt: 1775443 sats hops: 6 ppm: 1361
p = 45.20% amt: 180000 sats hops: 6 ppm: 1347
Attempt Summary:
=================
Tried to deliver 29091333 sats
expected to deliver 10573496 sats (36.35%)
actually deliverd 17857288 sats (61.38%)
deviation: 1.69
planned_fee: 42911.104 sat
paid fees: 26748.241 sat
Runtime of flow computation: 0.09 sec
================================================================
Round number: 2
Try to deliver 11234045 satoshi:
Statistics about 10 candidate onions:
successful attempts:
--------------------
p = 65.99% amt: 740000 sats hops: 3 ppm: 1381
p = 70.60% amt: 2076764 sats hops: 4 ppm: 1417
p = 51.08% amt: 1870235 sats hops: 4 ppm: 1466
p = 33.32% amt: 1423236 sats hops: 5 ppm: 1360
p = 58.33% amt: 84619 sats hops: 5 ppm: 1378
p = 42.70% amt: 488031 sats hops: 9 ppm: 1359
failed attempts:
----------------
p = 74.67% amt: 399134 sats hops: 3 ppm: 1757
p = 84.86% amt: 825478 sats hops: 3 ppm: 1836
p = 34.33% amt: 2355557 sats hops: 3 ppm: 1537
p = 28.37% amt: 970991 sats hops: 4 ppm: 1378
Attempt Summary:
=================
Tried to deliver 11234045 sats
expected to deliver 5724478 sats (50.96%)
actually deliverd 6682885 sats (59.49%)
deviation: 1.17
planned_fee: 16607.774 sat
paid fees: 9427.854 sat
Runtime of flow computation: 0.10 sec
================================================================
Round number: 3
Try to deliver 4551160 satoshi:
Statistics about 16 candidate onions:
successful attempts:
--------------------
p = 78.72% amt: 153600 sats hops: 2 ppm: 1341
p = 76.73% amt: 360000 sats hops: 2 ppm: 2572
p = 78.84% amt: 142257 sats hops: 2 ppm: 1415
p = 76.63% amt: 160000 sats hops: 2 ppm: 1382
p = 78.27% amt: 176000 sats hops: 3 ppm: 1439
p = 73.21% amt: 300000 sats hops: 3 ppm: 1460
p = 90.20% amt: 52822 sats hops: 3 ppm: 1362
p = 97.89% amt: 25478 sats hops: 3 ppm: 1487
p = 74.75% amt: 400000 sats hops: 4 ppm: 1436
p = 70.53% amt: 240000 sats hops: 5 ppm: 1375
p = 72.77% amt: 400000 sats hops: 5 ppm: 1359
p = 46.36% amt: 472297 sats hops: 9 ppm: 1359
failed attempts:
----------------
p = 77.32% amt: 194198 sats hops: 3 ppm: 1537
p = 60.40% amt: 320000 sats hops: 4 ppm: 1562
p = 41.05% amt: 724412 sats hops: 5 ppm: 1378
p = 31.23% amt: 430096 sats hops: 10 ppm: 1368
Attempt Summary:
=================
Tried to deliver 4551160 sats
expected to deliver 2815353 sats (61.86%)
actually deliverd 2882454 sats (63.33%)
deviation: 1.02
planned_fee: 6832.375 sat
paid fees: 4446.099 sat
Runtime of flow computation: 0.09 sec
================================================================
Round number: 4
Try to deliver 1668706 satoshi:
Statistics about 5 candidate onions:
successful attempts:
--------------------
p = 78.59% amt: 140800 sats hops: 3 ppm: 1438
p = 93.77% amt: 194198 sats hops: 4 ppm: 1378
p = 73.87% amt: 240000 sats hops: 5 ppm: 1361
p = 37.17% amt: 901708 sats hops: 10 ppm: 1366
failed attempts:
----------------
p = 72.08% amt: 192000 sats hops: 5 ppm: 1375
Attempt Summary:
=================
Tried to deliver 1668706 sats
expected to deliver 943618 sats (56.55%)
actually deliverd 1476706 sats (88.49%)
deviation: 1.56
planned_fee: 2293.679 sat
paid fees: 2029.679 sat
Runtime of flow computation: 0.09 sec
================================================================
Round number: 5
Try to deliver 192000 satoshi:
Statistics about 1 candidate onions:
successful attempts:
--------------------
p = 88.00% amt: 192000 sats hops: 2 ppm: 1382
Attempt Summary:
=================
Tried to deliver 192000 sats
expected to deliver 168960 sats (88.00%)
actually deliverd 192000 sats (100.00%)
deviation: 1.14
planned_fee: 265.344 sat
paid fees: 265.344 sat
Runtime of flow computation: 0.05 sec
================================================================
SUMMARY:
========
Rounds of mcf-computations: 5
Number of onions sent: 61
Number of failed onions: 19
Failure rate: 31.15%
total runtime (including inefficient memory managment): 3.945 sec
Learnt entropy: 79.93 bits
Fees for successfull delivery: 42917.217 sat --> 1475 ppm
used mu: 1
As @C-Otto asked me yesterday what this means for setting ppm with respect to channel size here are a few comments:
We can now express the maximum ppm so that a channel is not pruned via the following thoughts:
channel_size = 10_000_000
uncertaint_cost_feature = log(1_400_000_000/channel_size)
# combined_cost = (1.6*log(ppm+1) + log(uncertaint_cost_feature))/2
# knowing that the threshold (20% percentile) is (given the current network) at 8 we can solve to
# ppm = 2**((combined_cost*2 - log(uncertaint_cost_feature))/1.6)-1
so the following code can be used or adopted to produce the diagram at the end that shows you what ppm you can currently set. Note that if users start doing this, this will yield feedback loops and potentially oscilations on the fee market. so please don't take this as a static recommendation:
channel_sizes = [x for x in range(1_000_000,200_000_000,1_000_000)]
ppms = []
for channel_size in channel_sizes:
uncertaint_cost = log(1_400_000_000/channel_size)
ppm = 2**((16 - log(uncertaint_cost))/1.6)-1
ppms.append(ppm)
plt.figure(figsize=(8,6))
plt.title("Maximum possible ppm (assuming pruned Pickhardt Payments) given capacity")
plt.plot(channel_sizes,ppms)
plt.xscale("log")
plt.xlabel("capacity")
plt.grid()
plt.ylabel("maximum possible ppm")
plt.show()

i'm trying to understand what's going on here. what does ppm mean in this context?
@JeremyRubin wrote:
i'm trying to understand what's going on here. what does ppm mean in this context?
Short answer:
ppm stands for parts per million and is the main component that contributes to the routing fees and usually the number that node operators modify on their channels to earn routing fees for providing liquidity. It is specifically defined in the bolts as [u32:fee_proportional_millionths] which is usually just abbreviated as ppm by node operators.
long answer and context:
sorry I should have given a bit more context in the issue. This is related to #11 where I introduce a full simulated implementation of our results that produce optimally reliable and cheap payment flows on the lightning network. The (hopefully) well documented notebook may be found at: https://github.com/renepickhardt/mpp-splitter/blob/pickhardt-payments-simulation-dev/Pickhardt-Payments-Simulation.ipynb The question is that we want to find a flow that minimizes both the cost of uncertainty of the liquidity and the routing fees that have to be paid. The problem can be approximated by a piecewise linearized min cost flow problem which I am doing in PR #11 .
However even linear min cost flow solvers are quite slow and thus one wishes to prune the problem.
I am suggesting to initially prune the problem by including the 20% cheapest channels (cheap as in both low uncertainty cost and low routing cost). There are more advanced ideas that would generalize from this and are hinted to in #13 . In all cases (the simple one described here, the advanced case and without pruning) we have a mathematical consequence. Since the linearized uncertainty cost is proportional to 1/capacity we can easily see that larger channels can charge a higher ppm and still be included to the problem. (But even without pruning the algorithm on the full problem would select a much larger channel over a slightly cheaper but smaller channel which means that nodes that provide a lot of liquidity have a competitive advantage from scaling effects)
going back to the original bitcoin white paper (sorry link not working in all juristictions) and its title
Bitcoin: A Peer-to-Peer Electronic Cash System
we can see that the idea was to create a peer to peer system. However the math of the current design of Lightning and the assumption that sending nodes seek the optimal solution to the min cost flow problem gives an economic advantage to node operators that provide more liquidity in comparison to node operators that provide less liquidity.
People may or may not see this to be an issue. Their opinion might correlate with the number of BTC they hold. So I think it would be good if people like me who don't have much Bitcoin could still participate in routing on the Network and compete against large scale LSPs who mathematically benefit from their higher liquidity. Thus I was thinking if one could create in analogy to mining pools decentralized routing nodes Several people would be able to provide their liquidity to a node. This can obviously done in a custodial way but I would like to have a non custodial version that does not require trust.
For any design that I had in mind the issue is always that with every channel update all participants of this decentralized node would have to sign which most likely reduces latency in routing. While latency is currently not officially used I belief it is only a matter of time and after I published this comment I heard from many LSPs that internally they already use Latency in routing decisions. So to not put users who combine their efforts at a disadvantage I was wondering if one could use option_upfront_shutdown_script as defined in BOLT02. The output in the commitment transactions would always go to an address specified at channel opening via option_upfront_shutdown_script. users would only sign of the BTC transaction if the channel opening request included this option_upfront_shutdown_script which wouuld point to an address that is controlled by all people. However the question remains how one would redistributed the funds fairly to all participants? This would have to be a percentage of each output but we don't know the outputs as they change with every channel state (and as stated before we do not wish to collect signatures for each channel update from all participants)
I currently don't know how to solve that problem with Bitcoin in its current form. My hope is that covenants may be of help but to be frank I am not even sure if I understand covenants and / or OP_CTV properly as of now (I am not that deep into the details of bitcoin since I am mainly working on reliability questions of layer two and are mainly blackboxing what is happening on Layer 1)
However the math of the current design of Lightning and the assumption that sending nodes seek the optimal solution to the min cost flow problem gives an economic advantage to node operators that provide more liquidity in comparison to node operators that provide less liquidity.
People may or may not see this to be an issue. Their opinion might correlate with the number of BTC they hold. So I think it would be good if people like me who don't have much Bitcoin could still participate in routing on the Network and compete against large scale LSPs who mathematically benefit from their higher liquidity. Thus I was thinking if one could create in analogy to mining pools decentralized routing nodes Several people would be able to provide their liquidity to a node. This can obviously done in a custodial way but I would like to have a non custodial version that does not require trust.
If my understanding is correct, it would seem your proposal can:
a) significantly increase the profitability of LSPs with greater liquidity b) potentially disadvantage smaller lightning nodes
However:
a) this disadvantage is mitigated if individual users lightning transactions can be "pooled" b) widespread pooling of individual users would benefit the efficiency of the lightning network as a whole c) the predominant current option for this is the use of major 3rd party regulated custodial exchanges, brokers, or custodians
Could the use of Federated Chaumian mints such as (Fedimint/Minimint) be a potential option? From a LSP perspective, fedimints can pool smaller bitcoin holder's liquidity, but the federated 2nd party trust model plus use of chaumian mints makes them less likely to overly centralise resulting in a balance between the extremes of individual lightning nodes and a few centralised regulated nodes and the lightning network scaling of individual privacy challenges that come about as a result.