Is it a right implementation for OC_NN?

[SpecialMOB]

Hello,

First, thank's for good works.

I have a question for implementation of the OC_NN loss function in this code.

I think the function "custom_ocnn_hyperplane_loss" In src.models.OneClass_SVDD denote the loss function for OC_NN, but this function's objective function looks different from the paper's equation (4). I feel this implementation is quite similar to original OC_SVDD.

Is it a right implementation for OC_NN?

[CA4GitHub]

@SpecialMOB I'm trying to understand this source code too.

Currently in OneClass_SVDD.py I see:

def custom_ocnn_hyperplane_loss(self):

        r = rvalue
        center = self.cvar
        # w = self.oc_nn_model.layers[-2].get_weights()[0]
        # V = self.oc_nn_model.layers[-1].get_weights()[0]
        # print("Shape of w",w.shape)
        # print("Shape of V",V.shape)
        nu = Cfg.nu

        def custom_hinge(y_true, y_pred):
            # term1 = 0.5 * tf.reduce_sum(w ** 2)
            # term2 = 0.5 * tf.reduce_sum(V ** 2)

            term3 =   K.square(r) + K.sum( K.maximum(0.0,    K.square(y_pred -center) - K.square(r)  ) , axis=1 )
            # term3 = K.square(r) + K.sum(K.maximum(0.0, K.square(r) - K.square(y_pred - center)), axis=1)
            term3 = 1 / nu * K.mean(term3)

            loss = term3

            return (loss)

        return custom_hinge

Re term1 and term2 being commented out, I'm guessing the author was testing turning off this regularization.

Re the term3 which is not commented out, I don't understand all of it's parts. Specifically, both of the K.square(r) terms. Where did these K.square(r) terms come from? In addition, the K.sum(K.max(...)) is not quite what I expected from the paper. Overall, I was expecting custom_ocnn_hyperplane_loss to look like eq 4 in the paper:

It's also not clear to me the use of X_n: vs x_n in the paper. Below shows cropped version of eq 3, which is what I think eq 4 should expand to (except the X_n: vs x_n issue/concern) to compare:

Is X_n: suppose to be a matrix where each col is some x_n? It seems like x_n should be a vector, but I'm not convinced from the notation.

[raghavchalapathy]

r = rvalue: is updated as a call back after every epoch; was experimenting with different cases ; if you could uncomment the relevant lines , you see the equation in the paper same as code; X_n is a matrix there is a notation issue in the paper

[CA4GitHub]

Thanks for your response! I'll look into the r = rvalue you mentioned.

Is the equation in the current source code for custom_ocnn_hyperplane_loss1 (see my comment above) supposed to be equation 3 in your paper? It seems like the equation in the code is more like equation 3 in Deep One-Class Classification.

Also, I would love to ask you another question or 2 to help me understand the paper & how I could implement the One-Class Neural Network algorithm correctly. Would you prefer I ask them in this same issue thread, in a new issue thread, or some other way like email? Thanks again!

[raghavchalapathy]

The OCNN is implemented correctly in the code, Deep One class classification tries to build a separate the points by a building a sphere, I also have a loss function implented for this as hypersphere in code. we follow an approach to separate points from the hyperplane from the origin.

[CA4GitHub]

I see the commented out #term1 and #term2 variables which look like those in eq 4 in your paper. However, the term3 implementation contains K.square(r) & some other values that don't seem to appear in eq 4 in your paper. I'll repeat term3's implementation here for convenience:

term3 =   K.square(r) + K.sum( K.maximum(0.0,    K.square(y_pred -center) - K.square(r)  ) , axis=1 )
# term3 = K.square(r) + K.sum(K.maximum(0.0, K.square(r) - K.square(y_pred - center)), axis=1)
term3 = 1 / nu * K.mean(term3)

I understand where the last part term3 = 1 / nu * K.mean(term3) fits into equation 4 in your paper. However, I don't see how either of the other 2 lines fit into equation 4 in your paper.

[CA4GitHub]

@raghavchalapathy I put some comments on the pic from your paper which might help me illustrate some other confusion I have:

[BenedictGreen]

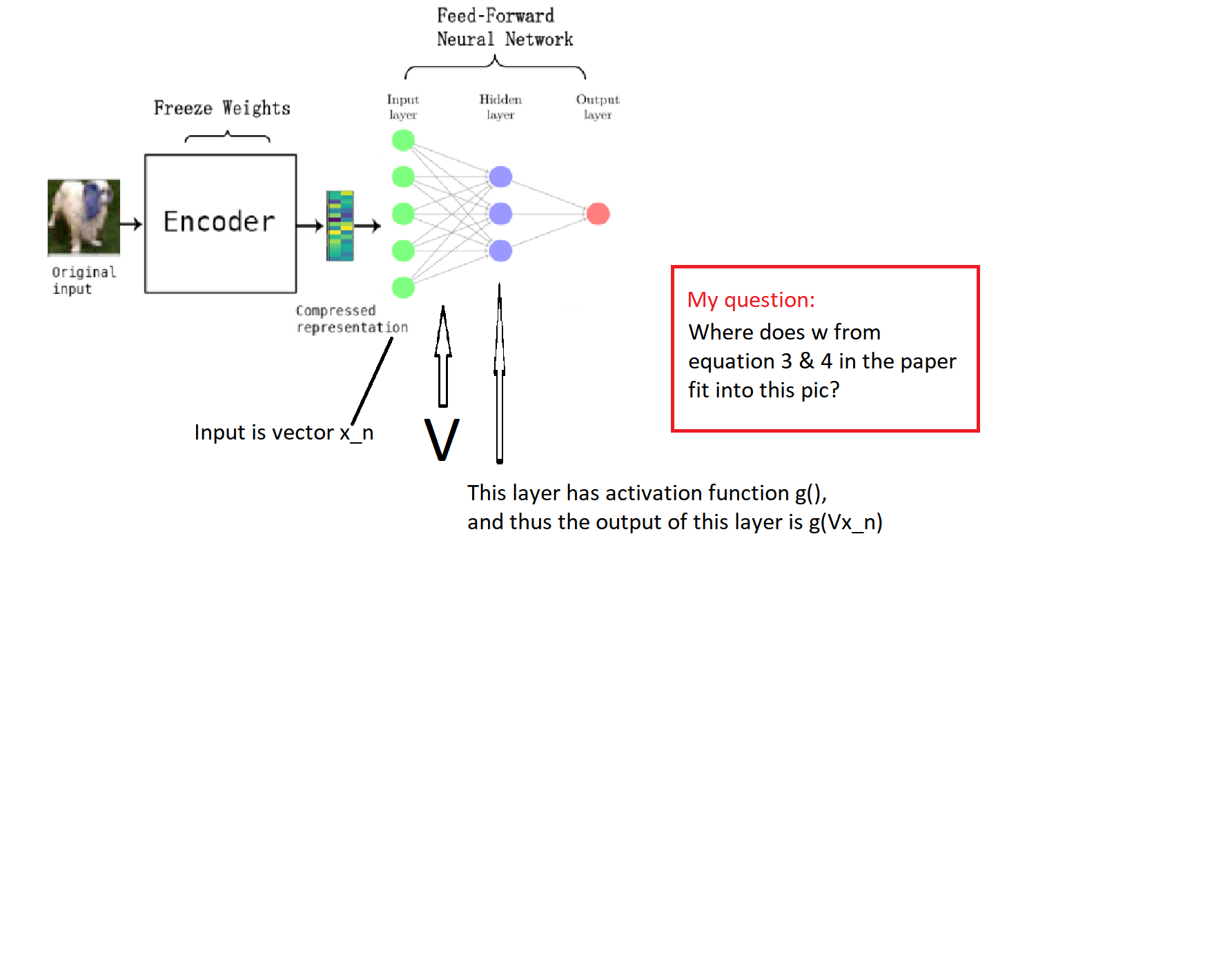
I see the commented out #term1 and #term2 variables which look like those in eq 4 in your paper. However, the term3 implementation contains K.square(r) & some other values that don't seem to appear in eq 4 in your paper. I'll repeat term3's implementation here for convenience:

term3 =   K.square(r) + K.sum( K.maximum(0.0,    K.square(y_pred -center) - K.square(r)  ) , axis=1 )
# term3 = K.square(r) + K.sum(K.maximum(0.0, K.square(r) - K.square(y_pred - center)), axis=1)
term3 = 1 / nu * K.mean(term3)

I understand where the last part term3 = 1 / nu * K.mean(term3) fits into equation 4 in your paper. However, I don't see how either of the other 2 lines fit into equation 4 in your paper.

Thanks to author for the good works. And the discussion between yours made me more clearly. @CA4GitHub ,I'm trying to understand this paper and source code too.And I got same question as you. In "OneClass_SVDD.py" as "custom_ocnn_hyperplane_loss(self):"in line886. the term3 implementation contains K.square(r) & some other values that don't seem to appear in eq 4 in the paper. I am as confused as you. I have thought about the discussion between you and author, but I still don't understand. Have you fix it out now?

Thanks again! Sincerely!

[mzietlow]

The loss function you see implemented in the code snippets posted above is taken from the paper 'Deep One-Class Classification' by Lukas Ruff et al. (2018). Here, a Hyper-Sphere is used as the decision boundary. For the Hyper-Plane loss function, I would like to point future readers towards ocnn.py.

Best wishes and good luck ~