Clarification in identification of estimands and estimation using backdoor.linear_regression

[codecD7]

I was going through the library code to better understand how the dowhy library works and explore causality in general. I came across a few questions in the identification and estimation step. Would be great if you could help me out with the understanding and reasoning behind these steps.

I have used the following graph for my exploration and have defined it using digraph:

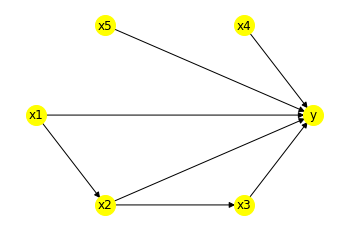
This is the code I am using for estimation:

causes = ['x2']
outcomes = ['y']

model = CausalModel(data = df, graph = Causal_Graph.replace("\n", " "), treatment = causes, outcome = outcomes)
model.view_model()

identified_estimand = model.identify_effect(method_name="exhaustive-search")
print(identified_estimand)

#regression
causal_estimate_reg = model_cg.estimate_effect(identified_estimand,
        method_name="backdoor.linear_regression",
        test_significance=True)
print(causal_estimate_reg)
print("Causal Estimate is " + str(causal_estimate_reg.value))

The output of the identification step is:

Estimand type: nonparametric-ate

Estimand : 1

Estimand name: backdoor Estimand expression: d
─────(Expectation(y|x4,x5,x1)) d[x₂]
Estimand assumption 1, Unconfoundedness: If U→{x2} and U→y then P(y|x2,x4,x5,x1,U) = P(y|x2,x4,x5,x1)

Estimand : 2

Estimand name: iv No such variable found!

Estimand : 3

Estimand name: frontdoor No such variable found!

The output of the estimation step is:

*** Causal Estimate ***

Identified estimand

Estimand type: nonparametric-ate

Estimand : 1

Estimand name: backdoor Estimand expression: d
─────(Expectation(y|x4,x5,x1)) d[x₂]
Estimand assumption 1, Unconfoundedness: If U→{x2} and U→y then P(y|x2,x4,x5,x1,U) = P(y|x2,x4,x5,x1)

Realized estimand

b: y~x2+x4+x5+x1+x2x4+x2x5 Target units: ate

Estimate

Mean value: 5.333333333333318 p-value: [0.]

These are the questions I have:

1. Why is the identification step considering x4 and x5 in the backdoor estimand? They are not related to x2 through any backdoor paths. They are effect modifiers and are considered as both observed common causes and effect modifiers in the code.

2. Why are all the backdoor paths not shown as estimands. With method_name = "exhaustive_search", it calculates all the backdoor path combinations and filters out some based on a set of rules. But it only outputs only the longest backdoor set, whereas in previous versions of the code it outputs all of them.

3. Why is x3 not considered as a front door estimand?

4. Why are the elements in the longest backdoor set considered as observed backdoor variables? Doesn't this imply that all the candidates for backdoor variables are chosen as observed backdoor variables?

5. Why is the child of x2 not being considered in the linear regression equation? Is it because backdoor.linear_regression only considers backdoor paths?

6. The example shown above is performed by specifying the graph. If we do not specify the graph, and specifying common causes, output, treatment and effect modifiers we cannot get the same graph. In fact, how do we even specify a child node if we are not giving a graph? If we specify x4 and x5 as effect modifiers in the second method (where we do not provide a graph), they are not even joined to the outcome and the results are different than expected. To get the same results as the first method the following image is of the graph that is generated in the second method.

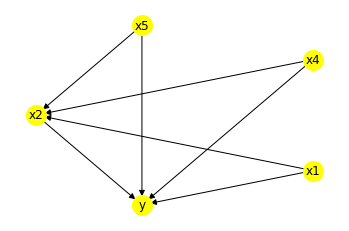
7. In the linear regression equation, why do we consider treatment * effect_modifer variables? Could you point me in the direction as to why this interaction is being considered?

[brendanflorez]

I'm new to DoWhy and Causal Inference so I may be missing something, but my problem seems the same as @codecD7 's points 1 and 2 above.

I have the following simple causal graph:

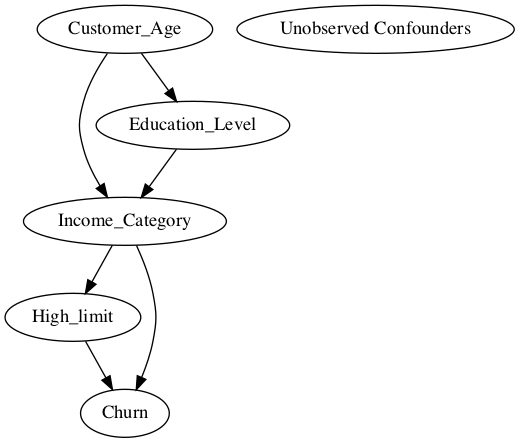
I want to find the total causal effect of High_Limit on Churn. Using the backdoor criterion it seems obvious I need to condition on Income_Category.

I have the following code:

causal_graph = """
digraph {
High_limit;
Churn;
Income_Category;
Education_Level;
Customer_Age;
U[label="Unobserved Confounders"];
Customer_Age -> Education_Level; Customer_Age -> Income_Category;
Education_Level -> Income_Category; Income_Category->High_limit;
High_limit->Churn; Income_Category -> Churn;
}

model = CausalModel(
            data = training,
            graph = causal_graph.replace("\n", " "),
            treatment = 'High_Limit',
            outcome = 'Churn')

estimands = model.identify_effect()
print(estimands)

This is what I get as my output:

`### Estimand : 1
Estimand name: backdoor
Estimand expression:
      d                                                                       
─────────────(Expectation(Churn|Education_Level,Income_Category,Customer_Age))
d[High_Limit]                                                                 
Estimand assumption 1, Unconfoundedness: If U→{High_Limit} and U→Churn then P(Churn|High_Limit,Education_Level,Income_Category,Customer_Age,U) = P(Churn|High_Limit,Education_Level,Income_Category,Customer_Age)

### Estimand : 2
Estimand name: iv
No such variable found!

### Estimand : 3
Estimand name: frontdoor
No such variable found!`

I don't understand why Estimand 1 is conditioning on all the variables when only Income_Category is needed?

To be clear, I had another person run this same code using an older version of DoWhy and he was able to generate E[Churn|Income_Category] as one of the backdoor options. However, when he updated to the latest version of dowhy he started getting the same answer as me.

[brendanflorez]

@codecD7 Did you ever figure this out?

[brendanflorez]

@amit-sharma any insight you could provide here would be helpful. Thank you to you and the team for all your great work on this!

[suryadipta]

I have been facing similar problems and will probably open up a new issue. DoWhy is a wonderful contribution to the research community and it will really help me a lot if I could get it working.

[amit-sharma]

The new dowhy version addresses most of these questions. I tried the following code, adapted from @codecD7

from IPython.display import Image, display
causes = ['x2']
outcomes = ['y']
graph = "digraph{{x1,x2,x3,x4,x5}->y;x1->x2;x2->x3}"
df=pd.DataFrame({
    'x1': np.random.random(100),
    'x2': np.random.random(100),
    'x3': np.random.random(100),
    'x4': np.random.random(100),
    'x5': np.random.random(100),
    'y':np.random.random(100)})
df['x2'] += df["x1"]
df['x3'] += df["x2"]
df['y'] += 0.2*df['x1'] + 0.2*df["x2"] + 0.2*df['x3'] + 0.2*df["x4"] + 0.2*df["x5"]
model = CausalModel(data = df, graph = graph.replace("\n", " "), treatment = causes, outcome = outcomes)
model.view_model()
display(Image(filename="causal_model.png"))

identified_estimand = model.identify_effect(method_name="exhaustive-search")
print(identified_estimand)

#regression
causal_estimate_reg = model.estimate_effect(identified_estimand,
        method_name="backdoor.linear_regression",
        test_significance=True)
print(causal_estimate_reg)
print("Causal Estimate is " + str(causal_estimate_reg.value))

The returned graph is,

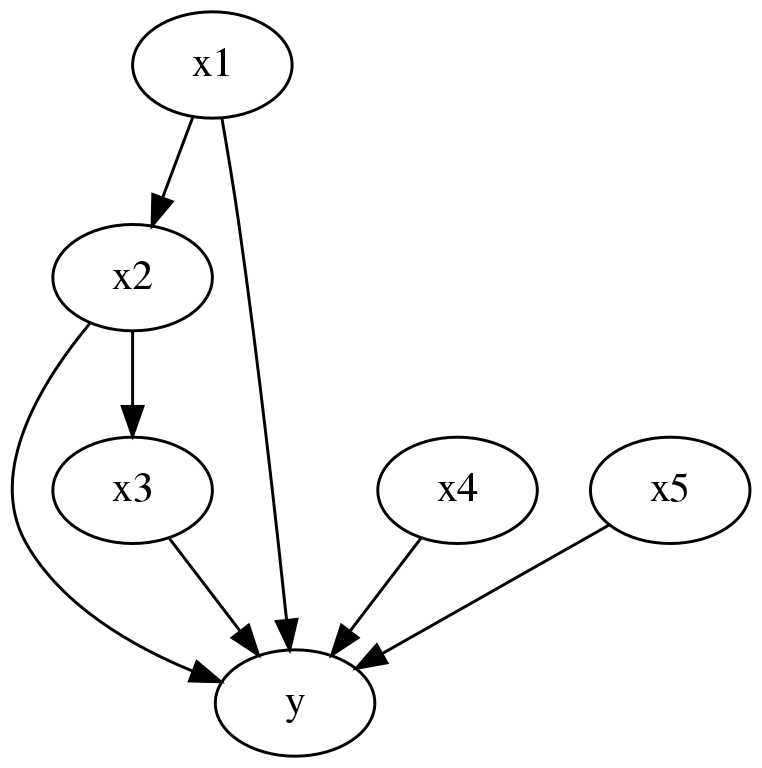
And the identification returns,

Estimand type: nonparametric-ate

### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d                     
─────(Expectation(y|x1))
d[x₂]                   
Estimand assumption 1, Unconfoundedness: If U→{x2} and U→y then P(y|x2,x1,U) = P(y|x2,x1)

### Estimand : 2
Estimand name: iv
No such variable(s) found!

### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!

Now answering the questions above,

Why is the identification step considering x4 and x5 in the backdoor estimand? They are not related to x2 through any backdoor paths. They are effect modifiers and are considered as both observed common causes and effect modifiers in the code.

Since DoWhy 0.7, there are four options for backdoor. "default", "exhaustive-default", "minimal-adjustment" and "maximal-adjustment". The code above shows a default backdoor set chosen from the exhaustive list based on heuristics.

Why are all the backdoor paths not shown as estimands. With method_name = "exhaustive_search", it calculates all the backdoor path combinations and filters out some based on a set of rules. But it only outputs only the longest backdoor set, whereas in previous versions of the code it outputs all of them.

If you want to see the full list, you can type,

identified_estimand.backdoor_variables

which returns,

{'backdoor1': ['x1', 'x4', 'x5'],
 'backdoor2': ['x1', 'x4'],
 'backdoor3': ['x1', 'x5'],
 'backdoor4': ['x1'],
 'backdoor': ['x1']}

Why is x3 not considered as a front door estimand?

Front-door criterion requires that all paths between treatment and outcome is mediated by x3. Here you have a directed edge from treatment and outcome too, that's why it is not considered as a front-door variable.

Why are the elements in the longest backdoor set considered as observed backdoor variables? Doesn't this imply that all the candidates for backdoor variables are chosen as observed backdoor variables?

No, only if the candidates satisfy the backdoor criterion. "maximal-adjustment" will return the maximal such set, while "minimal-adjustment" will return the minimal set.

Why is the child of x2 not being considered in the linear regression equation? Is it because backdoor.linear_regression only considers backdoor paths?

Yes. Considering the child of x2 will bias the estimation of total effect of x2, which is the default. It may be useful if the goal is to estimate direct effect, but then you need to use a different method.

The example shown above is performed by specifying the graph. If we do not specify the graph, and specifying common causes, output, treatment and effect modifiers we cannot get the same graph. In fact, how do we even specify a child node if we are not giving a graph? If we specify x4 and x5 as effect modifiers in the second method (where we do not provide a graph), they are not even joined to the outcome and the results are different than expected. To get the same results as the first method the following image is of the graph that is generated in the second method.

Specifying common_causes, etc. is a convenient way to express the most common graphs. It cannot specify all general graphs. Inputting graphs is the recommended way to use dowhy.

In the linear regression equation, why do we consider treatment * effect_modifer variables? Could you point me in the direction as to why this interaction is being considered?

In linear models, effect modification can be captured through interaction terms.