Proper concurrent handling of `BoundPeer`s in `KBucket`s

[greymistcube]

Seems like usage of ConcurrentDictionary<K, V> for a capped size dictionary is not enough. Aside from the operations for mutating the internal dictionary of a KBucket under current implementation not being atomic, there seems to be no easy way to implement such functionality simply by using ConcurrentDictionary<K, V>.

Given bucket size n, a key value pair (k, v), we need something like TryAddOrUpdate() which does the following in one go:

• If k is in the bucket, update its value to v.
• Else, if the bucket isn't full, add (k, v).
• Else, fail.

[greymistcube]

Additionally, how to resolve a possible race condition is not fully specified in the original paper and seems somewhat implementation specific. Consider the following scenario:

• Node A makes a request.
• Try to add A to bucket K_B.
  • Bucket K_B is full.
  • Ping K_B's oldest node X.
• While waiting for a reply, node X makes a request.
  • Update X's status in K_B.
  • X is no longer the oldest node in K_B.
• Node A makes another request.
• Try to add A to bucket K_B since there is no special pending status.
  • Bucket K_B is still full.
  • Ping K_Bs oldest node, which is now Y.
• Both pings to X and Y fail.
• Remove X and Y from K_B and add A "twice".
  • Since K_B is a dictionary, adding A twice just overwrites A's status on the second try.

Somehow we've managed to remove two nodes in order to add in a single node to K. This is just an example implementation where things could go "wrong".

[greymistcube]

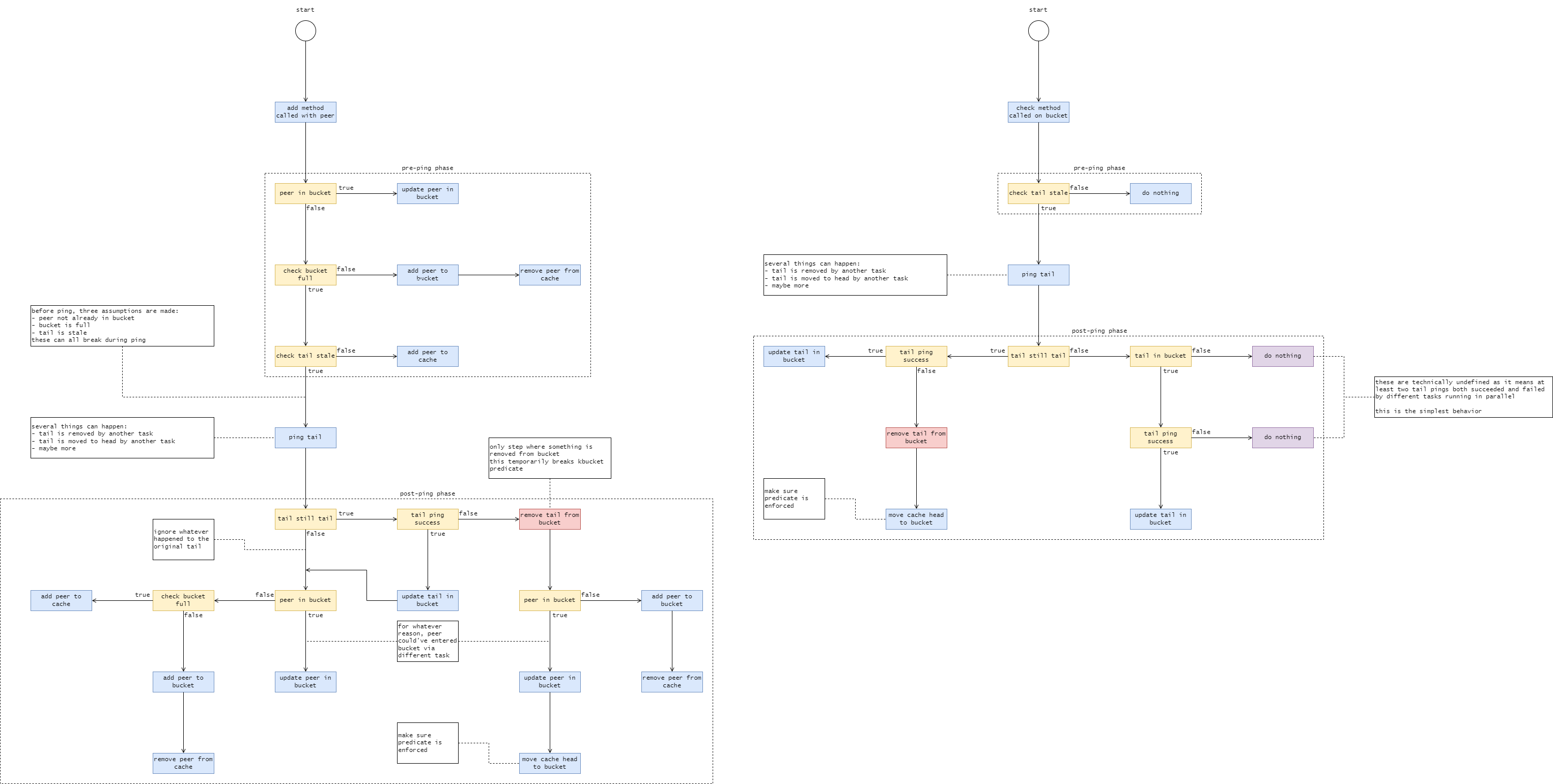
I think I have most things ironed out. Diagram was getting a bit unwieldy to use a mermaid diagram. 😕

Although most mentions of $k$-bucket make it seem like a trivial entity as a part of Kademlia protocol, it is not. This is mainly because most discussions revolve around pinging being an instantaneous process. With multiple tasks having race conditions, all, if not most, assumptions before ping can break while waiting for a response, or lack there of. 😐

There are a few things that can get more streamlined, such as reordering of conditionals, in the diagram above, and some steps require additional clarification.

As for actually implementing the logic for KBucket, as the logic is rather substantial, KBucket would need its own Ping() method, probably as a wrapped ITransport.SendMessageAsync().

[greymistcube]

Just writing down some working definition so that everyone can be on the same page. I think the definition below is not unreasonable and is mostly intuitive, but this might just be my personal opinion. If anybody has a different idea, please leave a comment. 😗

PS. Sorry, I ran out of alphabets while further formulating the properties of $k$-bucket, so started calling it $n$-bucket instead.

PPS. Comment rendering is different from markdown file rendering so word-wrapping is a bit off. I'm too lazy to edit them.

PPPS. If implemented properly, $k$-bucket can (and perhaps should) be implemented without any async.

---

Peers

Let $P$ be the set of all peers[^1] and $T$ be the set of all timestamps. Let $T$ have canonical ordering, i.e. for $t_{1}, t_{2} \in T$, $t_{1} < t_{2}$ if $t_{1}$ is an earlier timestamp to $t_{2}$.

A timestamped peer is any element $\hat{p} = (p, t) \in P \times T$. Let $\hat{p}, \hat{q}$ be two timestamped peers. We define an equivalence relation $\sim$ as

$$ \hat{p} \sim \hat{h} \iff p = h. $$

That is, $\hat{p}$ and $\hat{q}$ are equivalent if and only if peers are the same. For example,

$$ (p, t_{1}) \sim (p, t_{2}) $$

for any $t_{1}, t_{2} \in T$.

Additionally, we let an ordering $<_{T}$ on $P \times T$ the ordering inherited from $T$. That is,

$$ (p, t) <_{T} (q, s) \iff t < s. $$

For example, we can have

$$ (p, t) =_{T} (q, t) $$

where $p \neq q$ as long as the timestamps are the same.

Buckets

Let $\varphi: P \times T \to P$ be the canonical projection map. That is,

$$ \varphi(p, t) = p. $$

A bucket is any finite $X \subsetneq P \times T$ with the following properties:

• Uniqueness under equivalence relation $\sim$:

$$ |\varphi(X)| = |X| $$

• Total ordering under $<_{T}$[^2]:

$$ \forall \hat{p}, \hat{q} \in X, \quad \hat{p} =_{T} \hat{q} \iff \hat{p} = \hat{q} $$

Colloquially, a bucket cannot contain two different timestamped peers with the same peer and no two timestamps can be the same for all timestamped peers.

We denote the set of all possible buckets as $\mathcal{B} \subseteq \mathcal{P}(P \times T)$.

Given bucket size $n$, we define an $n$-bucket to be a tuple of buckets $B = (R, C)$, where $R$ is called the real bucket of $B$ and $C$ is called the cache bucket of $B$, with the following properties:

• Size limit $n$ on $R$ and $C$:

$$ \begin{align*} R = {\hat{p_{i}} = (p_{i}, t_{i}) \in P \times T : 1 \leq i \leq k} \quad&\mathrm{where}\quad |R| = k \leq n \ C = {\hat{q_{j}} = (q_{j}, s_{j}) \in P \times T : 1 \leq j \leq l} \quad&\mathrm{where}\quad |C| = l \leq n \end{align*} $$

• Disjointness between $R$ and $C$[^3][^4]:

$$ \varphi(R) \cap \varphi(C) = \varnothing $$

• Fill priority of $R$ over $C$:

$$ |R| < n \implies |C| = 0 $$

We say bucket $X$ of an $n$-bucket is full if $|X| = n$.

[^1]: The term peer is only used for the context of peer-to-peer network. From theoretical point of view, it can be any chunk of data, such as a bytestring. [^2]: Although strictly not necessary, this is to simplify further theoretical formulation by making head and tail functions well-defined. Without this requirement, the natural ordering induced by $<_{T}$ on $P \times T$ would be a preorder where minimum may not be defined to be unique for a set of peers. When implementing, selecting any minimal element should suffice. [^3]: The requirement is not necessary. In fact, the idea of a replacement cache in an $n$-bucket is not mentioned in the original paper. This, in theory, should help the routing table to be more populated, but the downside is, of course, having another point of logical complication. [^4]: It is possible to do away with this requirement, but when moving a peer from the cache bucket to the real bucket, it would require to loop through the cache bucket.