Wrong position of a point using the "scale" option

[AlainMatthes]

The problem

Without the use of scale=1.25 the searched point D has coordinates (18,0) but with scale=1.25 the displayed point is not exactly at the right place. The position of the point is correct if I use the option transform canvas ={scale=1.25} but this causes complications on the bounding box. Is there a way to get around this?

Minimal working example (MWE)

\documentclass[landscape]{article} 
\usepackage{tikz,fullpage}
 \usetikzlibrary{calc} 
\begin{document} 

\begin{tikzpicture}[scale=1.25]
  \draw[help lines](0,0) grid (18,1);
  \coordinate(A) at (0,0);
  \coordinate(C) at (10,0);
  \coordinate(B) at (6,0);
  \path (A) -- (B) coordinate[pos=.5](E);
  \path (B) -- (C) coordinate[pos=.5](F);
  \path[coordinate] let 
    \p1 = ($ (B) - (E) $),
    \n1={veclen(\x1,\y1)},
    \p2 = ($ (B) - (F) $),
    \n2={veclen(\x2,\y2)},
     in (barycentric cs:E={-\n2/1cm},F={\n1/1cm}) coordinate (D);
  \foreach \point in {A,B,C,D,E,F}
     \fill [black,opacity=.5] (\point) circle (2pt);
\end{tikzpicture}

\end{document}

[muzimuzhi]

It's the result of accumulated rounding errors. With scale=1 (the default) and scale=1.25, the coordinate B is at (170.71646pt, 0.0pt) and (170.74771pt, 0.0pt), respectively. Almost in-distinguishable difference. But after some computation, coordinate D is at (512.14938pt, 0.0pt) and (513.18889pt, 0.0pt), respectively. Not in-distinguishable anymore.

Loading tikz library fpu then adding /pgf/fpu/install only={reciprocal} to the tikzpicture env seems to work. Coordinate computations involving nodes (and coordinates) use reciprocal internally and fpu increases its accuracy.

Full example

\documentclass[landscape]{article}
\usepackage[margin=1cm, paperwidth=50cm]{geometry}
\usepackage{tikz}
\usetikzlibrary{calc, fpu} 

% add pins to named nodes
% code: https://github.com/muzimuzhi/latex-examples/blob/master/utilities/tikz-auto-mark-nodes.tex
% doc: https://github.com/muzimuzhi/latex-examples#utilitiestikz-auto-mark-nodestex
\InputIfFileExists{tikz-auto-mark-nodes.tex}{}{}

\makeatletter
% helper
\def\shownodecenter#1{%
  \pgf@process{\pgfpointanchor{#1}{center}}%
  \pgferror{point #1: (\the\pgf@x, \the\pgf@y)}%
}
\makeatother

\begin{document}
\raggedleft

\def\test#1{%
  \begin{tikzpicture}[#1]
    \draw[help lines](0,0) grid (18,1);
    \coordinate(A) at (0,0);
    \coordinate(C) at (10,0);
    \coordinate(B) at (6,0);
    \path (A) -- (B) coordinate[pos=.5](E);
    \path (B) -- (C) coordinate[pos=.5](F);
    \path[coordinate] let 
      \p1 = ($ (B) - (E) $),
      \n1={veclen(\x1,\y1)},
      \p2 = ($ (B) - (F) $),
      \n2={veclen(\x2,\y2)},
       in (barycentric cs:E={-\n2/1cm},F={\n1/1cm}) coordinate (D);
    %%% begin debug
    \shownodecenter B
    \shownodecenter D
    %%% end debug
    \foreach \point in {A,B,C,D,E,F}
       \fill [black,opacity=.5] (\point) circle (2pt);
  \end{tikzpicture}\par}

\test{auto mark/.try}
\test{auto mark/.try, scale=1.25, /pgf/fpu/install only={reciprocal}}
\test{auto mark/.try, scale=1.75, /pgf/fpu/install only={reciprocal}}
\end{document}

[AlainMatthes]

I agree with you about accumulated rounding errors, nevertheless I wonder about two points I noticed. First, if we use a scale that is a power of 2 there is no error, e.g. scale=2. Then why transform canvas={scale=1.25} also makes the error disappear.

In my example the error is minimal but with complex figures obtained with tkz-euclide, they become annoying. I had already tried to use fpu but not with the install only option which indeed seems to work.

[muzimuzhi]

Can you try this patch? It reduces (but not totally avoids) the inaccuracy introduced by four consecutive multiplied-by-0.1. It seems to solve the problem with scale=1.25, but i'm sure it won't work for all cases.

\usepackage{xpatch}
\makeatletter
\xpatchcmd\pgfmathreciprocal@@
  {\[email protected]\pgfmath@y\[email protected]\pgfmath@y\[email protected]\pgfmath@y\[email protected]\pgfmath@y}
  {\pgfmath@y\dimexpr\pgfmath@y/10000\relax}
  {}{\PatchFailed}
\makeatother

diff --git a/tex/generic/pgf/math/pgfmathfunctions.basic.code.tex b/tex/generic/pgf/math/pgfmathfunctions.basic.code.tex
index 1607c386..8aa03888 100644
--- a/tex/generic/pgf/math/pgfmathfunctions.basic.code.tex
+++ b/tex/generic/pgf/math/pgfmathfunctions.basic.code.tex
@@ -238,10 +238,7 @@
                 \multiply\c@pgfmath@counta-10000\relax%
                 \advance\c@pgfmath@countb\c@pgfmath@counta%
                 \pgfmath@y\c@pgfmath@countb pt\relax%
-                \[email protected]\pgfmath@y% Yes! This way is more accurate. Go figure...
-                \[email protected]\pgfmath@y%
-                \[email protected]\pgfmath@y%
-                \[email protected]\pgfmath@y%
+                \pgfmath@y\dimexpr\pgfmath@y/10000\relax
                 \advance\pgfmath@x\pgfmath@y%
             \fi%
         \fi%

[hmenke]

@muzimuzhi I have a similar idea some time ago https://github.com/hmenke/pgf/commit/50778951982497e0999aae8aff419cccc75fd334 (which you are already aware of because you commented on it).

Note that \dimexpr a*b and \dimexpr a/b will use TeX's fixed point arithmetic whereas \dimexpr a*b/c will use double precision floating point for the intermediates and then truncate (or round?) and convert back to fixed point. Depending on the case that could produce a decent accuracy improvement.

Demo

\documentclass{article}
\usepackage{tikz}
\begin{document}
\makeatletter
\newdimen\a
\newdimen\b
\foreach \x in {0.0001, 0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0} {
  \a=\x pt
  \b=1.2345 pt
  \makebox[3.5cm][l]{%
    dimexpr = \strip@pt\dimexpr 1pt * \a / \b\relax
  }
  \makebox[3.5cm][l]{%
    \pgfmathdivide{\x}{1.2345}
    PGF = \pgfmathresult
  }
  \makebox[3.5cm][l]{%
    LUA = \directlua{tex.sprint(tostring(\strip@pt\a / \strip@pt\b))}
  }
  \par
}
\end{document}

Excerpt from the e-TeX manual

Emphasis mine.

[AlainMatthes]

@muzimuzhi The patch is very interesting, it gives good results for the few figures that I had problems with! @hmenke Thanks for the demo file, your comment about dimexpr is very interesting

[muzimuzhi]

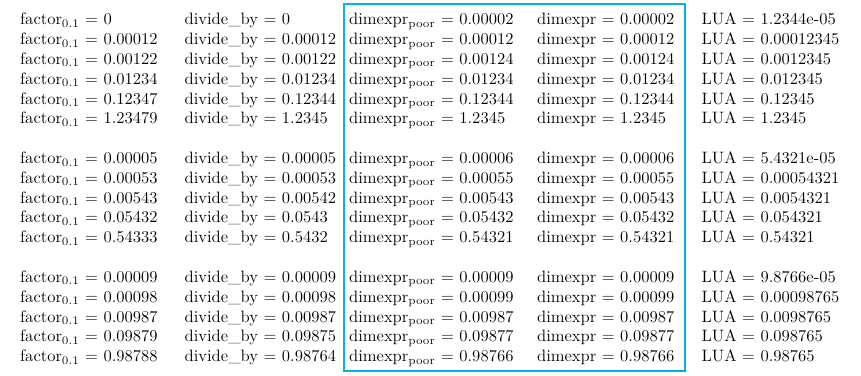
Sorry for late comment. Just for being divided by 10000, it seems the poor \dimexpr a/b is as accurate as \dimexpr a*b/c.

Tests using

\foreach \x in {0.12345, 1.2345, 12.345, 123.45, 1234.5, 12345,
                0.54321, 5.4321, 54.321, 543.21, 5432.1,
                0.98765, 9.8765, 98.765, 987.65, 9876.5}
{ compute \x/10000 in different ways }

% !TeX TS-program = lualatex
\documentclass[landscape]{article}
\usepackage{tikz}
\begin{document}
\newcommand\mybox[2][3.5cm]{\hbox to #1{#2\hss}\ignorespaces}

\makeatletter
\newdimen\a
\newdimen\b

\foreach \x in {0.12345, 1.2345, 12.345, 123.45, 1234.5, 12345,
                0.54321, 5.4321, 54.321, 543.21, 5432.1,
                0.98765, 9.8765, 98.765, 987.65, 9876.5}
{
  \a=\x pt
  \b=10000pt
  \ifdim\a<1pt \bigskip\fi\leavevmode
  \mybox{\a=.1\a \a=.1\a \a=.1\a \a=.1\a factor\textsubscript{0.1} = \strip@pt\a}
  \mybox{\divide\a by 10000 divide\_by = \strip@pt\a}
  \mybox[4cm]{dimexpr\textsubscript{poor} = \strip@pt\dimexpr \a / 10000\relax}
  \mybox{dimexpr = \strip@pt\dimexpr 1pt * \a / \b\relax}
  \mybox{LUA = \directlua{tex.sprint(tostring(\strip@pt\a / \strip@pt\b))}}
  \par
}
\end{document}