Add a `symmetric` keyword to Domain predicates

[keenancrane]

Is your feature request related to a problem? Please describe.

Mathematical relations, such as predicates, often have important properties such as reflexivity, transitivity, symmetry, etc. Yet Domain schemas currently support only a generic predicate type. The lack of such properties can make it difficult or impossible to implement some common pattern matches, especially if one wishes to avoid redundant code.

As a real motivating example, consider the structural-diagrams example, which includes types

type Atom
type Hydrogen <: Atom
type Oxygen <: Atom
predicate Bond( Atom a1, Atom a2 )

In this domain, we can construct a water molecule in a variety of ways, e.g.,

Hydrogen H1, H2
Oxygen O
Bond( O, H1 )
Bond( O, H2 )

or

Hydrogen H1, H2
Oxygen O
Bond( H1, O )
Bond( O, H2 )

etc.

Suppose that in Style we now want to enforce the constraint that the bond angle for a water molecule is 104.5 degrees. Our first attempt is

forall Oxygen o; Hydrogen h1; Hydrogen h2
where Bond(o,h1); Bond(o,h2) {
   -- enforce the bond angle
}

However, this pattern will match only the first version of our code, not the second. Currently the only solution is to duplicate the code:

forall Oxygen o; Hydrogen h1; Hydrogen h2
where Bond(o,h1); Bond(o,h2) {
   -- enforce the bond angle
}
where Bond(h1,o); Bond(o,h2) {
   -- enforce the bond angle
}

Of course, even this modified code doesn't cover all cases.

Describe the solution you'd like One possibility is to allow a Domain predicate to be tagged with additional properties. For instance, we might write

symmetric predicate Bond(Atom a1, Atom a2)

The semantics here are that Bond holds for either ordering of the arguments. More generally, symmetric would most naturally indicate that the order of arguments is irrelevant, for any number of arguments.

Another natural property (though perhaps more difficult to handle) is transitive. For instance, consider the predicate

transitive predicate P(T x, T y)

and the associated Substance program

T x, y, z
P( x, y )
P( y, z )

In this case, the following Style pattern

forall T u; T v
where P(u,v)

would match not only on u=x,v=y and u=y,v=z, but also (by transitivity) u=x,v=z. In this case it would not match on u=y,v=x (since it's not symmetric), nor on u=x,v=x (since it's not reflexive).

(These examples are meant only to stimulate thinking about how predicates could be better designed… lots of questions to still think about here.)

Describe alternatives you've considered Currently the solution is to duplicate code (see above).

Additional context This issue is related to (but distinct from) #290.

[keenancrane]

Here's another example, from examples/triangle-mesh-2d/triangle-mesh-2d.sty. The goal is to draw a line for any edge shared by two triangles:

-- Draw a thin line for any edge shared by two triangles
forall Triangle s; Triangle t; Vertex i; Vertex j; Vertex k; Vertex l
where s := MakeTriangle(i,j,k); t := MakeTriangle(j,i,l) {
   
   shape edgeSegment = Line {
      start: i.center
      end: j.center
      color: Colors.black
      thickness: .5*Global.lineThickness
   }
}

However, the selector will only match in the very particular case where the vertices of both triangles appear in exactly the given order. For instance, if you permute ijk or jil (even by an even permutation) then the match fails.

The issue of even vs. odd permutations is also a common one. For instance, when talking about a tensor A you say that it's fully symmetric if its value remains unchanged under any permutation of the inputs, and fully antisymmetric if a permutation of its inputs affects only the sign: negative for an odd permutation, positive (i.e., unchanged) for an even permutation. In the scenario above, the question of even vs. odd permutation is also natural, because an even vs. odd permutation of the vertices of an oriented simplex (like a triangle) will preserve vs. reverse its orientation. The relative orientations of two simplices in turn are a key property that often needs to be indicated in a diagram. For this, we could introduce a detail keyword even, e.g.,

even symmetric constructor MakeTriangle( Vertex i, Vertex j, Vertex k ) -> Triangle.

In this case, a Style selector that includes

where s := MakeTriangle(i,j,k); t := MakeTriangle(j,i,l) {

would match on, say, ijk and ilj, but not ijk and ijl.

[keenancrane]

Note that one way to match on symmetric predicates would be to implement Boolean logic a la #775, and then expand a symmetric predicate into a collection of or statements. For instance,

where P(x,y); P(y,z)

becomes

where (P(x,y) and P(y,z)) or (P(x,y) and P(z,y)) or (P(y,x) and P(y,z)) or (P(y,x) and P(z,y))

However, this is not how we should implement it, because it leads to a combinatorial explosion (especially for predicates with more arguments, or longer lists of predicates in the where clause). It's also unnecessary—for instance for a pair of symmetric predicates

symmetric predicate P(x,y,z)
symmetric predicate Q(x,y,z)

and a selector

forall T x; T y; T z; T w
where P(x,y,z); Q(y,z,w)

we are essentially just asking whether the sets {x,y,z} and {y,z,w} intersect in a pair of elements {y,z}, which can be determined by checking, for each element of the first set, whether it appears in the second one. More explicitly, we can sort the two argument lists lexicographically. Then, starting with the first element of the first list we check if it appears in the second list. If so, we locally label it as y. Then we move on to the next element of the first set, until we find a second match, which we label z. Or we fail to find y and z, in which case the match fails. Since the sorting takes O(n log n) time and the scanning takes O(n) time, the whole check takes O(n log n) time—much better than the exponential cost of expanding all permutations of the arguments into a Boolean expression!

[christianp]

I don't know if I'm doing things in an awkward way, but I think this would also be useful for constructors. I have two types, Point and Edge, and I have constructor MkEdge(Point, Point) -> Edge. This effectively represents a relation on points, which for an undirected graph should be symmetric. I copied this from the graph theory DSL in the examples directory.

This could be a predicate, pretty much exactly as @keenancrane described above, but I have a feeling that if I wanted to draw a graph and its dual, the constructor method would lead to shorter code. I'll have a go and see!

(and if it's just as easy with a predicate: what's the point of constructors?)

[keenancrane]

I'm running into this issue again—seems to be quite common in real examples.

Here's the specific use case this time around: I have a domain where there are Vertices, and then Edges and Triangles are described as pairs or triples of Vertices, respectively. I also have a Corner type defined by three vertices. Most importantly, each Edge e is associated with some angle e.alpha that determines how much this edge "bends". The diagrams look something like this:

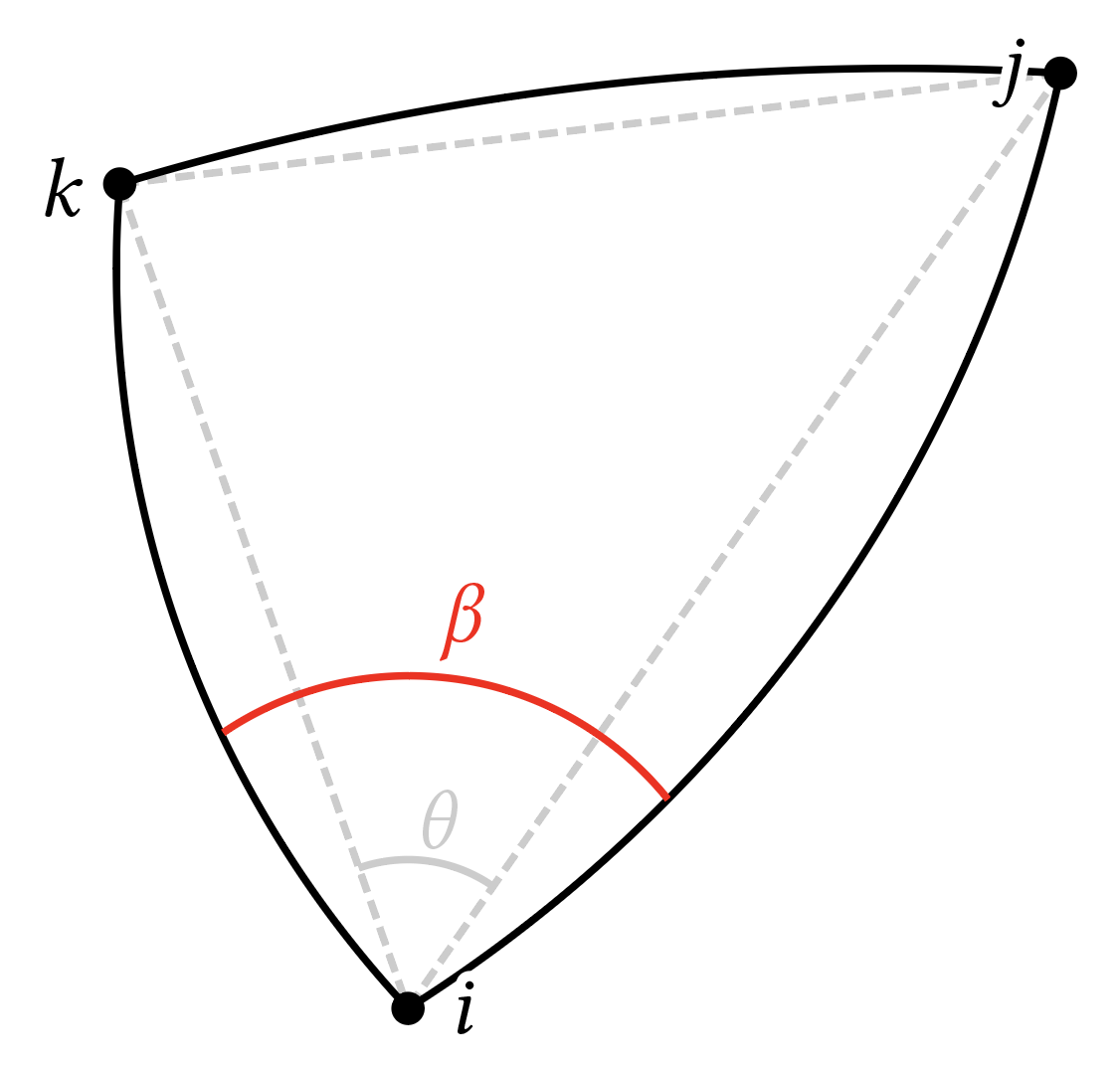
It's easy enough to draw the angle θ between the straight edges, since here I need only data associated with the vertices. So, I can just write a selector like this one:

forall Corner c; Vertex i; Vertex j; Vertex k
where c := Corner(i,j,k) {

But suppose I want to draw the red arc, labeled β, between the two "bent" edges (which here I've added in Adobe Illustrator, on top of a Penrose diagram). Then I really need access to the data on edges. But a match like this one won't work:

forall Corner c; Vertex i; Vertex j; Vertex k; Edge e1; Edge e2
where c := Corner(i,j,k); e1 := MakeEdge(i,j); e1 := MakeEdge(i,k) {
-- (access e1.alpha and e2.alpha to draw the corner arc)

The problem is that each of the edges could have been made in either order, e.g., e1 := MakeEdge(i,j) or e1 := MakeEdge(j,i). So, with this setup, you would need to write redundant rules that match on all possible permutations of orderings:

where c := Corner(i,j,k); e1 := MakeEdge(i,j); e1 := MakeEdge(i,k) {
where c := Corner(i,j,k); e1 := MakeEdge(j,i); e1 := MakeEdge(i,k) {
where c := Corner(i,j,k); e1 := MakeEdge(i,j); e1 := MakeEdge(k,i) {
where c := Corner(i,j,k); e1 := MakeEdge(j,i); e1 := MakeEdge(k,i) {

[liangyiliang]

Hello! I have some ideas about how we would implement symmetric predicates.

Augmenting the Substance Program

Suppose we have programs.

-- dsl.dsl
type Atom
type Oxygen <: Atom
type Hydrogen <: Atom
symmetric predicate Bond (Atom, Atom)

-- sub.sub
Oxygen O
Hydrogen H
Bond (H, O)

The current issue is that the following Style program

-- sty.sty
forall Oxygen O; Hydrogen H
where Bond (O, H) {
  // ...
}

will not match the Bond (H, O).

I'm currently thinking about internally "augmenting" the Substance program during the Substance compilation phase into something like

-- augmented_sub.sub
Oxygen O
Hydrogen H
Bond (H, O)
Bond (O, H) -- this line is augmented by the Substance compiler because `Bond` is symmetric

Using this augmentation, though the previous Style program will not match Bond (H, O), it will certainly match the augmented Bond (O, H) and hence draw things correctly.

Possible Issues

This does, however, lead to some potential issues. For example, suppose we have a dummy example

-- dsl.dsl
type MyType
symmetric predicate MyPred(MyType, MyType)

-- sub.sub
MyType x
MyType y
MyPred (x, y)

-- sty.sty
forall MyType x; MyType y
where MyPred(x, y) {
  // ... drawing something
}

If we augment our Substance program, we have

MyType x
MyType y
MyPred (x, y)
MyPred (y, x) -- this is augmented

Then, the Style program will match both applications of MyPred, even though one of them is not specified by the programmer, and hence will render the same thing twice. I'm not sure if this is the desired behavior.

Also, does it really make sense for MyPred(MyType, MyType) to be symmetric, given that both of its arguments are of the exact same type?

Crux of Problem

I think the center of this problem is, what does it mean for predicates to be symmetric?

1. Is it in the sense of matching (i.e. Bond(H, O) should match both Bond (H, O) and Bond (O, H))?
2. Or, are we talking about the mathematical meaning of symmetric relations, i.e. if Bond(H, O) holds, then Bond(O, H) necessarily holds, and if MyPred(x, y) holds, then MyPred(y, x) necessarily holds too?

The second point corresponds to the proposed solution of augmenting the Substance program. I think the second point implies the first point, but not necessarily vice versa. This question also influences which component handles symmetry: the first point hints at the Style matcher handling symmetry, whereas the second point suggests, as I proposed, the Substance compiler handling symmetry.

I also imagine that the approach of augmenting the Substance program will also work for partial symmetries and transitive predicates.

[keenancrane]

Three comments:

1. My gut feeling is that we should really implement symmetric matching directly, rather than using a "kludge" like augmenting the Substance program. Because, as you say, there are inevitably unintended consequences to the latter approach—like a rule being invoked multiple times when it should only be invoked once.

2. The symmetry really seems to pertain to the full selector, and not just a single predicate within the selector. Consider for instance the selector

forall Oxygen o; Hydrogen h1; Hydrogen h2
where Bond( o, h1 ); Bond( o; h2 ) {
   ...
}

Since both Oxygen and Hydrogen are subtypes of Atom, the predicate Bond is defined for a generic (Atom,Atom) pair. The issue here is that, without symmetric matching, the selector is looking for a very particular type signature: (Oxygen,Hydrogen) and (Oxygen,Hydrogen). But we want to allow other possibilities, like (Hydrogen,Oxygen) and (Oxygen,Hydrogen). I think @wodeni and/or @samestep will have to provide some guidance on how to actually implement something like this; I don't know the internals of the new Style compiler well enough to say anything useful!

3. It does make sense to talk about symmetry even when all arguments have the same type, again because you're trying to allow permutations in the context of a larger selector. Consider the triangle example from above:

forall Corner c; Vertex i; Vertex j; Vertex k; Edge e1; Edge e2
where c := Corner(i,j,k); e1 := MakeEdge(i,j); e1 := MakeEdge(i,k)

Here, both Corner and Edge are predicates on either two or three instances of Vertex. But the point is that there needs to be the freedom to permute the arguments in one predicate relative to another. (I agree that if there's one and only one binary symmetric predicate, then nothing more is needed to make this predicate symmetric.)

[liangyiliang]

I agree on the third point. On the second point, I would also argue that the approach of augmenting Substance works.

Hydrogen H1, H2
Oxygen O
Bond( H1, O )
Bond( O, H2 )

will become

Hydrogen H1, H2
Oxygen O
Bond( H1, O )
Bond( O, H2 )
Bond( O, H1 ) -- augmented
Bond( H2, O ) -- augmented

and

forall Oxygen o; Hydrogen h1; Hydrogen h2
where Bond( o, h1 ); Bond( o; h2 ) 

then matches the second and third Bond(...) applications in the augmented Substance program.

But overall, I do understand that this method feels more like a "hack" to the process due to its potential unintended consequences.

[keenancrane]

Yeah, creating multiple instances of the same predicate seems like trouble…

[liangyiliang]

Partially resolved with basic binary symmetric predicates