Can't return solution of coupled differential equations

[cgiovanetti]

I'm trying to solve a mid-sized system of coupled differential equations with diffrax. I'm using version 0.2.0. Here's a short snippet of dummy code that raises the issue I'm having:

import jax.numpy as jnp
from diffrax import diffeqsolve, ODETerm, Kvaerno3,PIDController

def Results():
    def Y_prime(t, Y, args):
        dY = jnp.array([Y[6], (Y[5]-Y[6])**2,Y[0]+Y[7], (Y[1])**2, Y[2],Y[3], Y[4]**3, Y[5]**2])
        return dY
        
    t_init = 100
    t_fin = 1e5

    Yn_i = 1e-5
    Yp_i = 1e-6
    Yd_i = 1e-12
    Yt_i = 1e-12
    YHe3_i = 1e-12
    Ya_i = 1e-12
    YLi7_i = 1e-12
    YBe7_i = 1e-12

    Y0=jnp.array([[Yn_i], [Yp_i], [Yd_i], [Yt_i], [YHe3_i], [Ya_i], [YLi7_i], [YBe7_i]])
    term = ODETerm(Y_prime)
    solver = Kvaerno3()
    stepsize_controller = PIDController(rtol=1e-8, atol=1e-8)
    t_eval = jnp.logspace(jnp.log10(t_init),jnp.log10(t_fin),num=100)
    sol_at_MT = diffeqsolve(term, solver, t0=jnp.float64(t_init), t1=jnp.float64(t_fin), dt0=jnp.float64((t_eval[1]-t_eval[0])/10),y0=Y0,stepsize_controller=stepsize_controller,max_steps=None)
    Yn_MT_f, Yp_MT_f, Yd_MT_f, Yt_MT_f, YHe3_MT_f, Ya_MT_f, YLi7_MT_f, YBe7_MT_f = sol_at_MT.ys[-1][0][0],sol_at_MT.ys[-1][1][0],sol_at_MT.ys[-1][2][0],sol_at_MT.ys[-1][3][0],sol_at_MT.ys[-1][4][0],sol_at_MT.ys[-1][5][0],sol_at_MT.ys[-1][6][0],sol_at_MT.ys[-1][7][0]

    Yn_f,Yp_f,Yd_f,Yt_f,YHe3_f,Ya_f,YLi7_f,YBe7_f = Yn_MT_f, Yp_MT_f, Yd_MT_f,Yt_MT_f,YHe3_MT_f,Ya_MT_f,YLi7_MT_f, YBe7_MT_f
    return jnp.array([Yn_f,Yp_f,Yd_f,Yt_f,YHe3_f,Ya_f,YLi7_f,YBe7_f])
Yn_f,Yp_f,Yd_f,Yt_f,YHe3_f,Ya_f,YLi7_f,YBe7_f = Results()
print(Yn_f)

It seems diffrax successfully solves the differential equation, but struggles to return the output, i.e. it seems the code hangs when trying to assign values to the variable sol_at_MT. Tampering a bit with the diffrax source, it looks like there are two things going on.

One is that, no matter what I try to return (even if I set all of the returns to None), if the lines right before the return in integrate.py

branched_error_if(
    throw & jnp.invert(is_okay(result)),
    error_index,
    RESULTS.reverse_lookup,
)

aren't commented out, the code will freeze. I can include a print statement right after these lines (just before the return) that prints out successfully even when they're not commented, but I can't assign anything to sol_at_MT in without the code hanging if these lines are left in.

Then, if I comment that branched_error_if() call out, the code still hangs if I try to return ts, ys, stats or result from integrate.py. This doesn't seem to be an issue of time or memory; the code just freezes up and can't even be aborted from the command line whether I'm running locally or with extra resources on a cluster.

[patrick-kidger]

What is the value of sol_at_MT.result if you pass diffeqsolve(..., throw=False)?

Also, which backend (CPU/GPU/TPU) are you using?

[cgiovanetti]

I've tried with both CPU and GPU and had the same result.

I can't access sol_at_MT.result; the code hangs before it finishes assigning values to that variable (setting throw=False doesn't seem to help with that). Best I can do is print out result directly from integrate.py, but there's no concrete value assigned yet, so the "value" right now is just

Traced<ShapedArray(int32[], weak_type=True)>with<DynamicJaxprTrace(level=0/1)>

[patrick-kidger]

Okay. So I'm finding that this code takes a very long time to run, as you've set tight tolerances and chosen a large integration time of 1e5. Can you provide a smaller example demonstrating the issue, that I can try to run?

What you're describing sounds pretty odd though. For example setting throw=False should effectively disable the branched_error_if block you've highlighted. How did you determine that commenting out this block might help?

By the way, if you're using float64 then you need to specifically enable this for JAX. See below for a complete example of a tidied-up version of your code. In addition, in case you've not seen it before, I've also left in one of my own debug statements of jax.experimental.host_callback.id_print, just to demonstrate how that can be used.

import jax
import jax.experimental.host_callback as hcb
import jax.numpy as jnp
from diffrax import diffeqsolve, ODETerm, Kvaerno3,PIDController

jax.config.update("jax_enable_x64", True)

def results():
    def y_prime(t, y, args):
        hcb.id_print(t)
        return jnp.stack([y[6], (y[5]-y[6])**2, y[0]+y[7], (y[1])**2, y[2],y[3], y[4]**3, y[5]**2])

    term = ODETerm(y_prime)
    solver = Kvaerno3()

    t0 = jnp.array(100, dtype=jnp.float64)
    t1 = jnp.array(1e5, dtype=jnp.float64)
    t_eval = jnp.logspace(jnp.log10(t0),jnp.log10(t1),num=100)

    y0_n = 1e-5
    y0_p = 1e-6
    y0_d = 1e-12
    y0_t = 1e-12
    y0_He3 = 1e-12
    y0_a = 1e-12
    y0_Li7 = 1e-12
    y0_Be7 = 1e-12
    y0 = jnp.array([y0_n, y0_p, y0_d, y0_t, y0_He3, y0_a, y0_Li7, y0_Be7], dtype=jnp.float64)

    stepsize_controller = PIDController(rtol=1e-8, atol=1e-8)
    sol = diffeqsolve(term, solver, t0=t0, t1=t1, dt0=(t_eval[1]-t_eval[0])/10, y0=y0,
                      stepsize_controller=stepsize_controller, max_steps=None)
    (y1,) = sol.ys
    return y1

y1_n, *_ = results()

[patrick-kidger]

In passing -- if you're trying to solve a stiff differential equation with an implicit solver, then it's often worth setting non-default values in the PIDController -- see here.

[cgiovanetti]

Thanks for the tip about the debug statement! Apologies about the float64 line missing--I pulled this snippet from a larger block of code and must have left that line out.

I don't think the original tolerances and interval were so extreme they should have caused the code to take a long time to run. i.e., if the branched_error_if block is commented out, and ts, ys, stats and result in integrate.py are all set to None, I find the solver actually finishes pretty quickly.

But using the debug statement, it looks like the solver hangs at a particular point around t of 176, give or take a few decimal places. So you could change t1 to 200, and maybe set rtol and atol to 1e-5, and you'll probably still get the same behavior I'm trying to describe. Something odd that's happening, though, is that leaving the debug statement in causes the solver to get stuck around t of 176, regardless of any of my commenting or returning None. Whereas if I leave the hcb.id_print(t) line out, I can get to the end of the script if I set ts, ys, stats and result to None.

I found the issue with the branched_error_if block by taking the very naive approach of commenting out chunks of the source code to find the piece that caused the code to hang. But I had also set all of the returns to None, so I do find that if I set throw=False and set ts, ys, stats and result to None, the code doesn't hang. So it seems returning these particular variables is the larger issue.

[patrick-kidger]

The fact that things finish fast when you comment out ts/ys/stats/result is to be expected. These are all of the outputs from the solver that depend on you actually solving a differential equation. I expect what's happening is that the JAX compiler is just deleting the entire differential equation solve, which is why things appear to work.

I think the fact that the solve can't progress past 176 is because the state explodes. If I change it to id_print((t, y)) then I start seeing e.g.

( 176.22964696                                                                                                                                       
  [7.18675227e+01 1.47735555e+19 1.21738049e+08 5.13855080e+26                                                                                       
 3.99147616e+01 2.11710976e+15 1.25960702e+03 1.47735555e+19] )

from which you can see that y is starting to take on some extremely large values, for which it's expected that things should go wrong. For example the implicit problem tackled at every stage of the solver may become unsolvable. Or perhaps you're just seeing finite-time blow-up of your differential equation. (Your vector field is non-Lipschitz, so there's no guarantee that your solution even exists.)

[cgiovanetti]

That's odd--I can solve this dummy system with scipy.integrate.solve_ivp in a few seconds. I use their built-in method BDF, but changing the PIDController tolerances to something smaller doesn't seem to resolve the issue, so I don't think it's a matter of just trying to solve a stiff system.

I can also modify this code to be a bit more realistic if you think the system I chose is the culprit in this example, but that seems unlikely to me; the behavior I'm seeing is the same whether I use this simple system or the more complicated system I want to work with.

[jaschau]

FWIW I previously also encountered similar issues - the solvimg would just insanely long - when using implicit solvers on a non-stiff system that worked just fine with explicit methods. So this might hint that there is indeed an issue with the implicit solvers - it might be coincidental though and unfortunately I cannot straightforwardly create a minimum working example at the moment.

[patrick-kidger]

For this particular example, switching to Dopri8 produces blow-up at the same point in time. So this won't be anything to do with implicit solvers.

[cgiovanetti]

I've found some other examples of systems that diffrax seems to have a hard time solving, in the hopes it might make the issue a little clearer. In particular, here's one that doesn't blow up too suddenly anywhere--most curves just trace exponentials:

def y_prime(t, y, args):
    return jnp.stack([y[3]/y[7], jnp.sqrt(y[2]), y[7]+y[0], y[1], y[0],y[6], y[5]/y[6], y[4]])

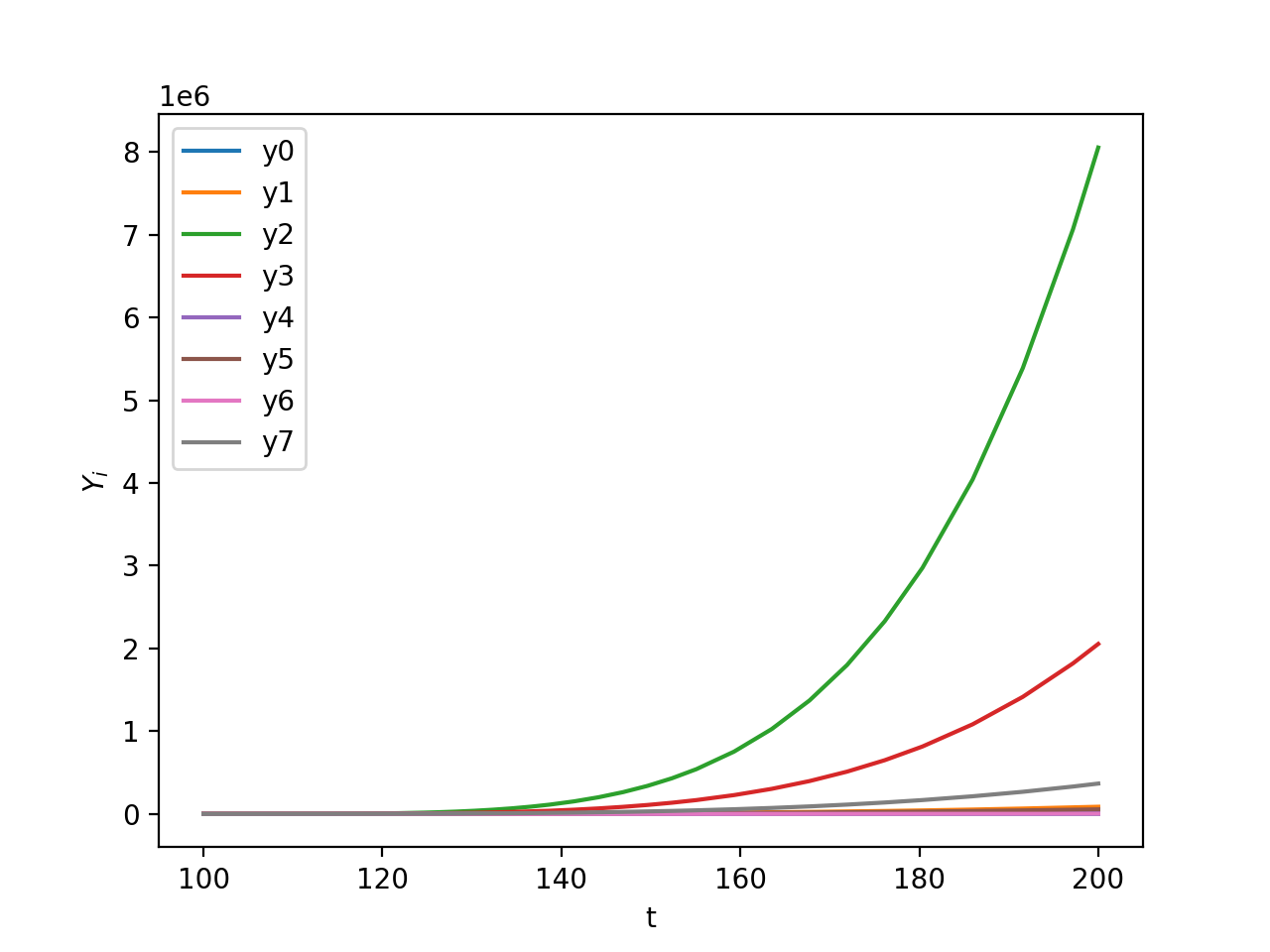
Using all of the same initial conditions etc. I specified above, solve_ivp can handle this one too without breaking a sweat: diffrax, however, doesn't even seem to be able to take the first few steps. I just get a bunch of nans in the output. This is what the diffrax system looks like just before it breaks:

( 100.07026054
[-1.03544580e-02  1.62113874e-06 -1.03083638e-07  8.96000308e-08
 -1.03083988e-07  1.27193046e-03  3.11953334e-02  1.01504118e-11] )

after which it looks like

( 100.07026054 [nan nan nan nan nan nan nan nan] )

and never recovers. Meanwhile I can differentiate the results of solve_ivp to recover the original equation, i.e.

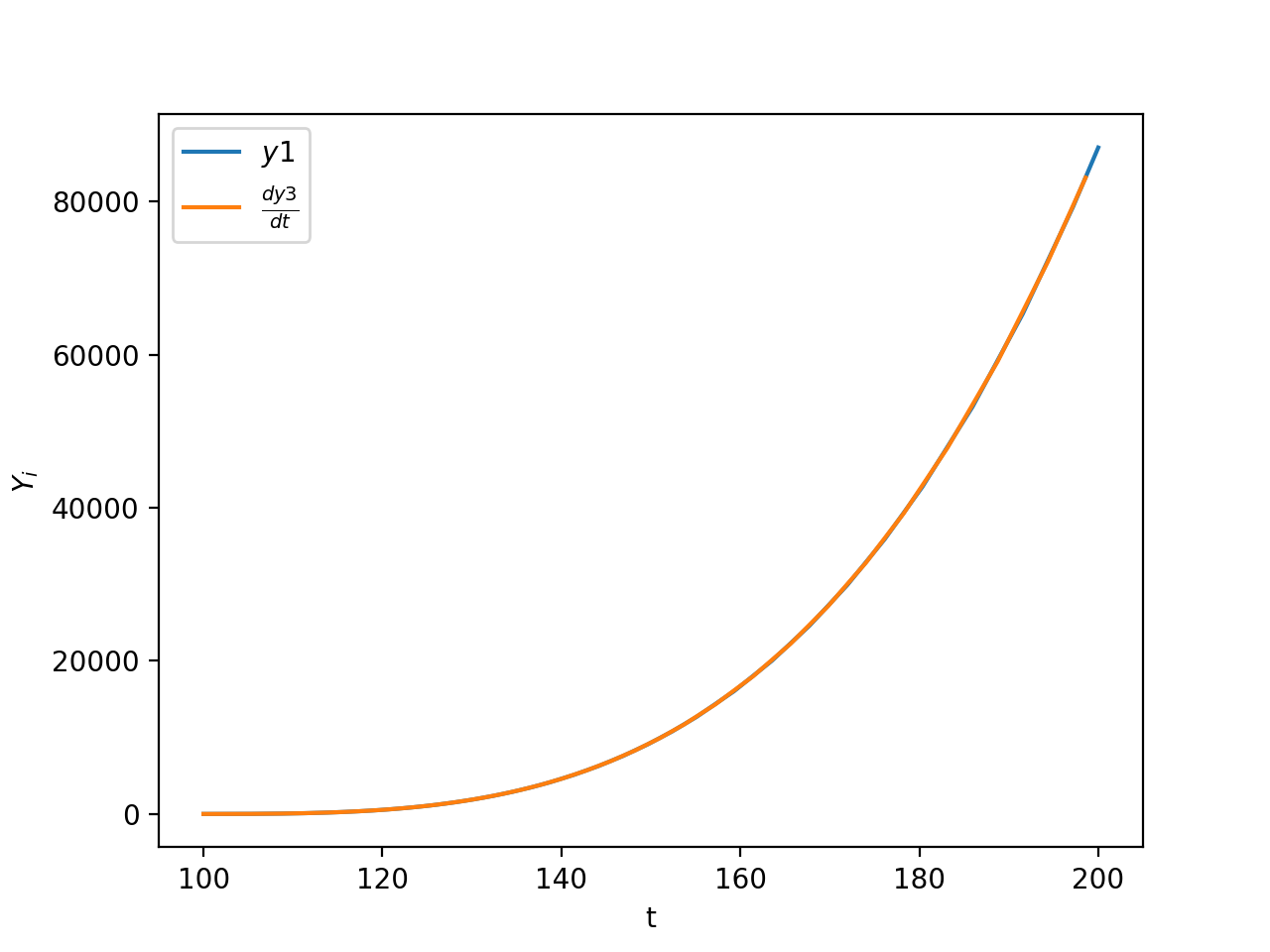
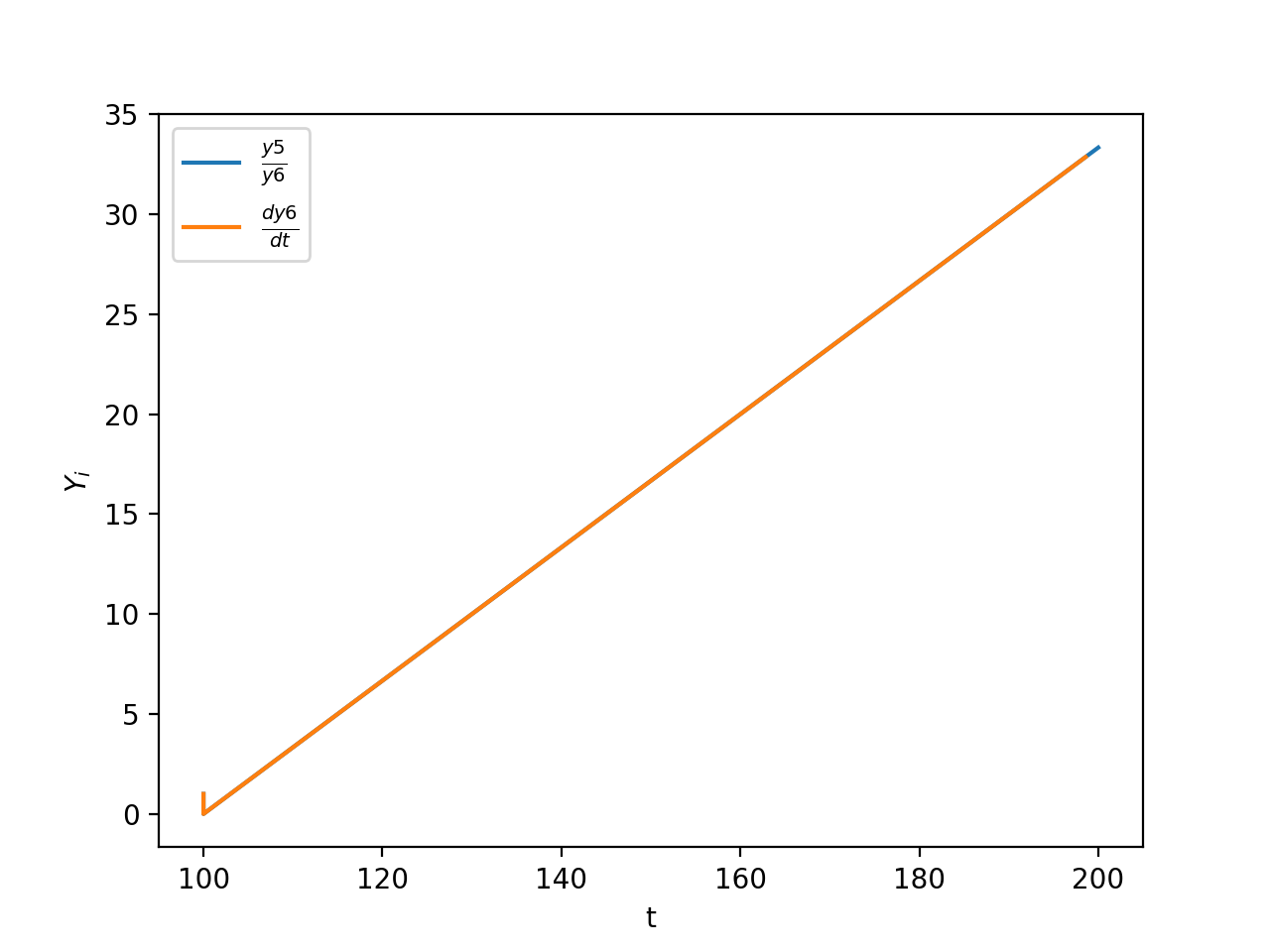
I'm not sure what gives solve_ivp the advantage here, but this system doesn't seem too pathological to me and I'm not sure why diffrax seems to have such a hard time with it.

[patrick-kidger]

It turns out that what is going on here is this:

1. The initial step size dt0 that is being passed into diffrax.diffeqsolve is very large. When the solver makes its first numerical step, using this step size, we end up in a nonphysical region of space for which y[2] is negative.
2. Too-large step sizes normally aren't a problem, as the stepsize controller will just reject these. Except the vector field for this system is sort-of-questionably-defined: it includes a square root, in particular jnp.sqrt(y[2]). And jnp.sqrt(something negative) produces a NaN.
3. Thus instead of seeing "this error is too large", the stepsize controller just sees a NaN, which it doesn't know how to handle, and the whole thing chokes.

As a general rule, you shouldn't use vector fields that are capable of returning NaNs: the NaN can propagate and break things in strange ways, as it has done here. (In this case, both the sqrt and the / are pretty suspicious.)

It's actually pretty hard to come up with a sensible policy for handling NaNs in all the various cases they might arise. Still, at least for this case it's clear that we want to reject the step -- I'll submit a PR soon so that diffrax.PIDController rejects steps in the event of a NaN.

For posterity, a couple of other solutions to this problem (right now, even without this upcoming PR):

1. Pass either dt0=None or dt0=something small: in this case we never end up in an unphysical region of space, things work as normal, and both Diffrax and solve_ivp obtain identical solutions.
2. Ensure that your vector field is never capable of returning a NaN. In your case, out = jnp.stack(...); return jnp.where(jnp.isnan(out), jnp.inf, out) will suffice.

[cgiovanetti]

Sorry it's taken so long for me to get back to you, just wanted to be sure this was also helping with the larger set of DEs I'm trying to solve. This is helpful, thanks!