does periodic need to be false for conservative?

[raphaeldussin]

https://github.com/pangeo-data/xESMF/blob/f9653558699d6a4da079088e9e77ec261458a0b7/xesmf/frontend.py#L206

I'm not sure this should be the case

[aulemahal]

As a test, I modified the current code so that we could have periodic grids with conservative. More precisely I commented the line referenced above and modified : https://github.com/pangeo-data/xESMF/blob/90d3c0ff3246c1c36f85a421792c274e001f3055/xesmf/backend.py#L215-L225 to

    #assert (grid.num_peri_dims == 0) and (
    #    grid.periodic_dim is None
    #), 'Cannot add corner for periodic grid'

    grid.add_coords(staggerloc=staggerloc)

    lon_b_pointer = grid.get_coords(coord_dim=0, staggerloc=staggerloc)
    lat_b_pointer = grid.get_coords(coord_dim=1, staggerloc=staggerloc)

    if grid.num_peri_dims > 0:
        lon_b_pointer[...] = lon_b[:-1, :]
        lat_b_pointer[...] = lat_b[:-1, :]
    else:
        lon_b_pointer[...] = lon_b
        lat_b_pointer[...] = lat_b

Then I made tests with

ds_in = xe.util.grid_global(2, 2)
ds_out = xe.util.grid_global(6, 6)
reg = xe.Regridder(di, do, 'conservative')
regp = xe.Regridder(di, do, 'conservative', periodic=True)

With an a uniform field we get strange results. For example:

da = np.zeros((90, 180)) + 1
d_per = regp(da)
d_nop = reg(da)

d_per and d_nop are equal everywhere except at the last column (last lon) where the difference is on the order of 1e-16. That difference is kinda linear with the uniform field value, going to 0 if da is all 0. More intringing: with da[:] = 1e15, the difference was:

array([ 0.   ,  0.25 ,  0.125,  0.25 ,  0.125,  0.25 ,  0.125,  0.25 ,
       -0.125,  0.125,  0.   ,  0.125,  0.125,  0.25 ,  0.25 ,  0.125,
        0.   ,  0.   ,  0.125,  0.125,  0.125,  0.25 ,  0.125,  0.375,
        0.25 ,  0.125,  0.25 ,  0.25 , -0.25 , -0.125])

This result was not random, it should be repeatable.

I'm not sure why the results would be different at all... When the bounds are given, shouldn't the regridding be the exact same? With the short analysis I just did, it seems the difference is on the order of machine precision for most use cases.

All this said, allowing periodic=True and requiring bounds is easily implementable, but a decision on which column of bounds to remove has to be made (I decided to remove the last column) and this decision makes a difference for fields with super large values.

[jsimkins2]

I can confirm that performing the changes @aulemahal demonstrated above works for an irregular grid. My motivation for using the periodic=True tag was due to dateline artifacts for a topography file that was regridded to an irregular Northeast Pacific grid.

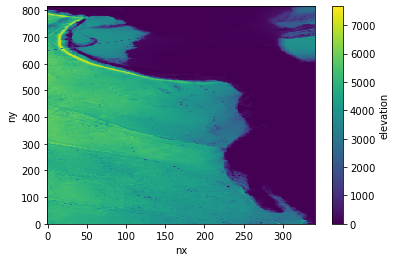
The dashed line at the top of the image represents the dateline issue. As mentioned above, setting the periodic argument to true is overwritten in xesmf.Regridder . I followed the steps above exactly and got the following result.

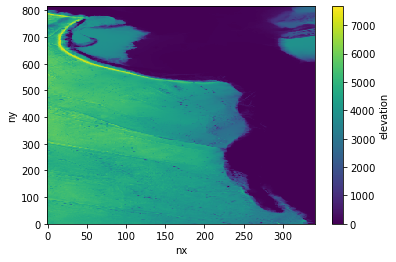
Here is the difference between the two images.