Question about bearing
Here's an example of a function I wrote using Pygeodesy. Given two lat/longs and a bearing direction from each, I find the intersection point.
def intersection_point(lat_long_1, bearing_1, lat_long_2, bearing_2):
vector1 = pygeodesy.sphericalNvector.LatLon(*lat_long_1)
vector2 = pygeodesy.sphericalNvector.LatLon(*lat_long_2)
return vector1.intersection(bearing_1, vector2, bearing_2)
The docstring for this function says bearing is measured relative to "North". Is it safe to say this is true north, not magnetic north?
Also, can I expect this function to be accurate in-real life? I just don't really understand all the jargon in the READMe. For my use case, I would walk onto a large field, get a GPS location and a bearing, walk 30 meters to another point and bearing, and then the intersection of the two lines would have a location. Would the result of my function be that location?
-
In all of PyGeodesy, north is True north at 0 degrees bearing.
-
Not sure about the
intersection_pointfunction and the description of the use case.
Function intersection_point computes the intersection of 2 lines, given as 2 bearings from 2 points.
The use case consists of 1 point, 1 bearing and 1 distance (30 meter). To compute the point after a given distance, use the destination method, example:
def destination_after(lat_lon, bearing, distance):
vector1 = pygeodesy.sphericalNvector.LatLon(*lat_lon)
return vector.destination(distance, bearing)
HTH
Sorry, I don't think I explained my use case well. Here is a picture:
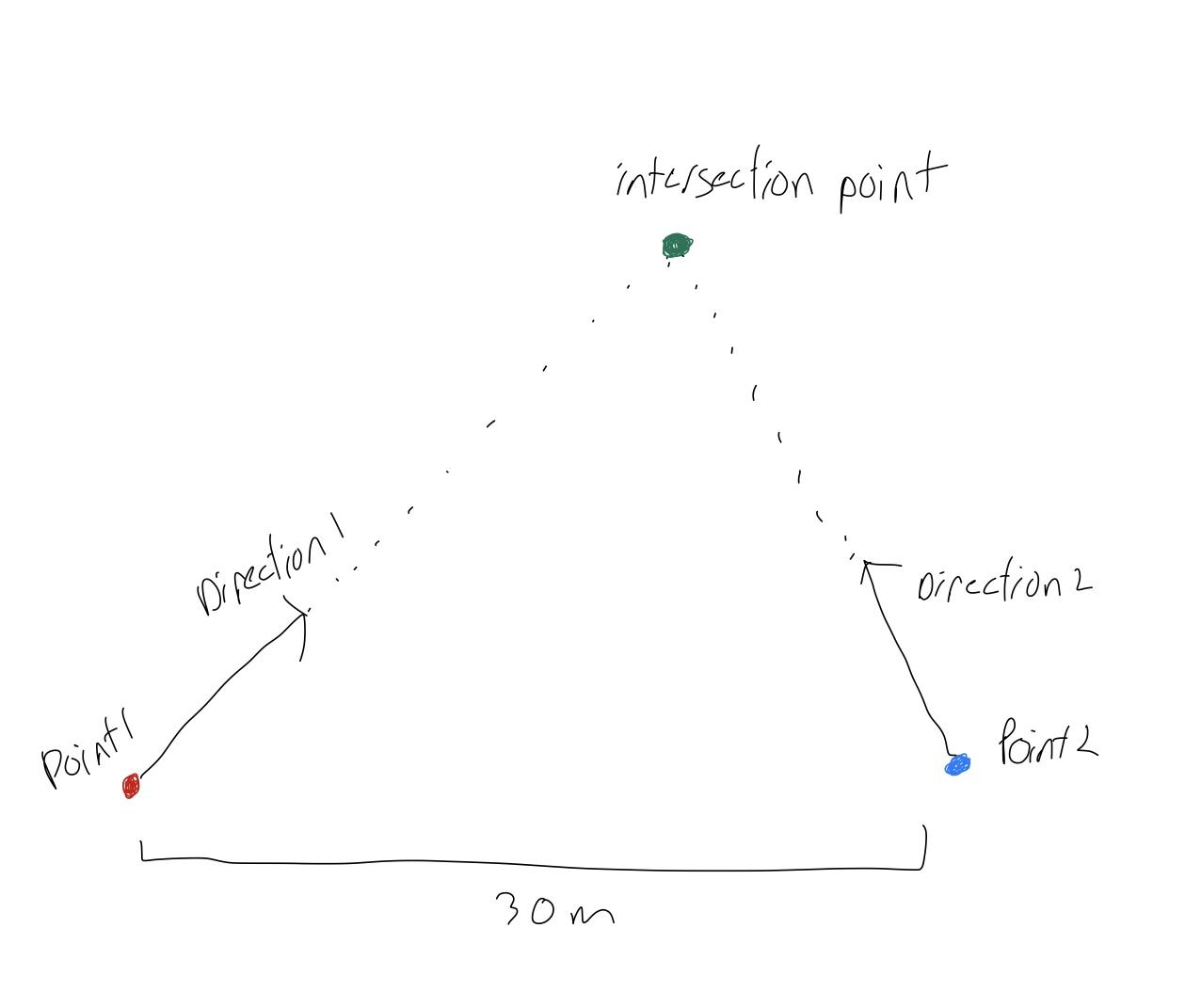
I believe this is the correct use case, I'm just not sure if I should be using the intersection function or if one of the other intersection functions is more accurate to real-world GPS coordinates.
In general and for longer distances the ellipsoidal functions are more accurate than the spherical ones. For shorter distances -say less than 100 km- the difference may be insignificant, but it depends on the use case.
For shorter distances -and certainly for 30 m- simple 2-d geometric would be applicable. See 3-d vector function intersection3d3 and set useZ=False.
There should -and soon will- be a function intersection2(lat1, lon1, bearing1, lat2, lon2, bearing2, …) to conveniently compute the lat-/longitude of the intersection.
Is there any disadvantage to using the ellipsoidal functions? Do they have the same signatures as the spherical ones?
All LatLon classes require a lat and lon value as the first 2 arguments. Additional arguments may be different but are optional and have reasonable default values.
Ellipsoidal intersections are computed iteratively and therefore take more time.
Use one of the ellipsoidal functions if the highest accuracy is needed and if the distance between the points and intersection can exceed, say 1,000 km.
One, arbitrary example. The intersection of (lat1=0, lon1=0, bearing1=30) and (lat2=0, lon2=0.000269, bearing2=-30) -with 0.000269 being about 30 m- from the ellipsoidal, spherical and Vector3d function is the same (lat=0.00023296083361801397, lon=0.00013449999999999996).
With lon2=0.01 or about 1 km, the 3 intersections are still the same (lat=0.008660254037844388, lon=0.005). The 3 intersections differ for lon2=5 degrees, or approx. 500 km and above.
For the given use case, 3-d function intersection3d3 is sufficient provided the intersection point is nearby. The forthcoming release 23.4.11 contains function intersection2(lat1, lon1, bearing1, lat2, lon2, bearing2, datum=None, ...)to compute the intersection point 4 different ways through the datum keyword argument.
Thank you. My only concern then, is the way latitude and longitude are specified. intersection3d3 seems to take cartesian points - would providing real-world lat,long work for that? If not, then I think it would be best for me to stick with spherical coordinates.
Use lon for x and lat for y, like the new function intersection2 does it internally. Get the .whl or .zip file from here to try intersection2 since 23.4.11 is not on PyPI yet.
Thank you. Last question, the data I'm getting for latitude and longitude are in degrees * 10 ^7, will these functions accept that, or do I need to convert to just degrees?
All lat-, longitudes and bearing in pygeodesy are in degrees (modulo 360). Angles named phi and lam (lambda) are lat- and longitudes in radians (modulo PI2). Distance, elevation, height, length, radius, etc. are in meter, conventionally.
Perhaps, use something like the following to keep all degrees 10^7-based around intersection2 ...
from pygeodesy import intersection2 # PyGeodesy 23.4.12 or later
def _e(f, e, *args):
for arg in args:
yield f(arg * e)
def intersection7(lat1, lon1, bearing1, lat2, lon2, bearing2):
args = _e(float, 1e-7, lat1, lon1, bearing1, lat2, lon2, bearing2)
elel = intersection2(*args) # or add ... datum=R_M or datum=-R_M
return tuple(_e(int, 1e7, *elel)) # 2-tuple (lat, lon) x 1e7
PyGeodesy 23.4.12 is available on PyPI and GitHub.
The new function intersection2 offers 5 different choices to compute an intersection, selected with the datum keyword argument. Use new keyword argument small to set an upper limit for "small" distances (in meter), default 100 Km.
HTH