Use np.linalg.multi_dot instead of multiple np.dot routines

[maldil]

Reference issue

Not a reported issue

What does this implement/fix?

It is more succinct and effective to refactor code to use np.linalg.multi_dot rather than numerous np.dot routines. What do you think about this change?

[welcome[bot]]

Hello! 👋 Thanks for opening your first pull request here! ❤️ We will try to get back to you soon. 🚴🏽‍♂️

[cbrnr]

Looks good to me!

[agramfort]

I am a bit relunctant to do these changes automatically. In the specific use cases here we know size of the matrices so we put the () at the right place so the order of the dots are optimal. To do these changes I would suggest you time in a real use case eg taking the examples that use these methods on real data and see how it affects the run time. Does it sound reasonable?

[drammock]

In the specific use cases here we know size of the matrices so we put the () at the right place so the order of the dots are optimal.

According to the docstring: "multi_dot chains numpy.dot and uses optimal parenthesization of the matrices". So we can probably trust that it won't slow things down, but I agree with @agramfort that it's worth a quick timing to make sure. I do think it's more readable than what we have now, although I'd argue it's less readable than using @:

CMinvG = np.dot(np.dot(U / (S + eps), U.T), G)  # current; hard to read
CMinvG = np.linalg.multi_dot([U / (S + eps), U.T, G])  # better
CMinvG = (U / (S + eps) @ U.T) @ G  # most readable?

[cbrnr]

If we're already benchmarking, if it turns out that @ is not significantly slower, I'd vote for that option because it's the best in terms of readability.

[larsoner]

AFAIK there isn't a mechanism for the __matmul__ / @ operator to modify the order of operations if it's chained, so it's very likely multiple @ will be slower than explicitly chosen parens or automatic resolution via multi_dot

[cbrnr]

Likely, but it would be better to check.

[maldil]

Do anybody know if these are square matrices? In another project, I had a good discussion regarding this, we discovered that multiple dot calls (what you already have in this project) perform well for square matrixes and multi_dot perform better for non-square matrixes. @ does not work well in either case.

[drammock]

we discovered that multiple dot calls perform well for square matrixes and multi_dot perform better for non-square matrixes. @ does not work well in either case.

Define what "works well" / "performs well" means here? Faster? Uses less memory? Less prone to programmer error? More numerically stable? Something else?

[maldil]

Sorry about not defining the terms. This is about time complexity. Did not analyze memory consumption or other things as you mentioned.

[drammock]

This is about time complexity

ok, well, quoting @larsoner:

it's probably worth some quick checks with arrays of these shapes to see if it's at least as good as what we had before. Let me know if you need help with this @maldil

So the next step is figure out what shapes these matrices have, and run some timing tests.

[agramfort]

this was brought by @maldil on the pyRiemann repo and see a quick benchmark I did:

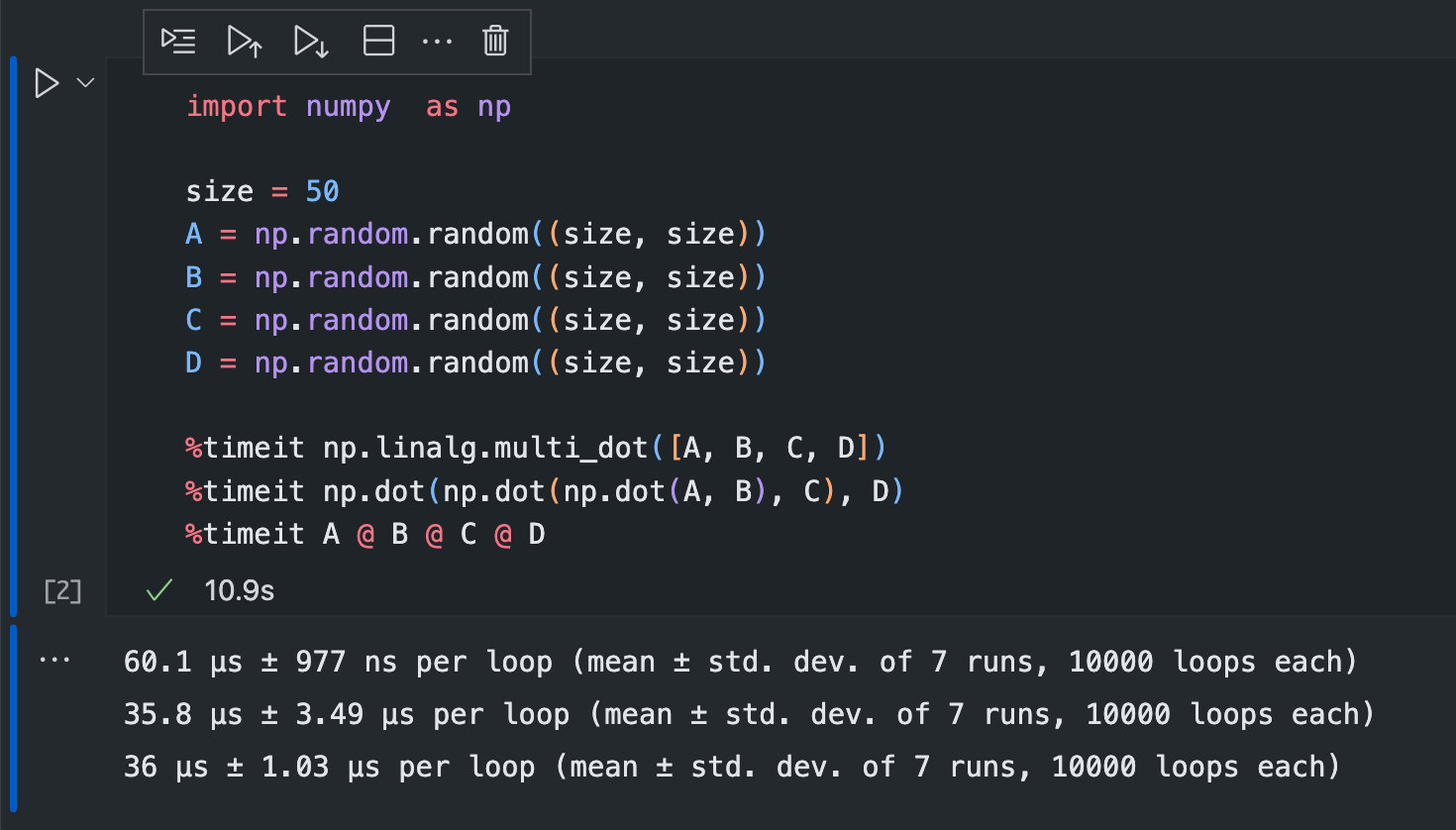
in other words it's not a silver bullet for all use cases

[larsoner]

Makes sense. Looks like there is ~30 uS overhead for deciding which order to use, so we'd only want to think about this if the sizes are big enough. More evidence that we need to look at the sizes in use in each case, and what sizes they can be at the extremes (given differences in numbers of source points and/or sensors)!

[maldil]

Yes, the sizes are sufficiently big enough, and it should perform well (in terms of time) for non-square matrices. I'm attempting to run test cases of the modified methods to determine matrices sizes and shapes. I am getting the following error. Anyone have any ideas? @larsoner

Dataset testing version 0.0 out of date, latest version is 0.137

Dataset out of date, force_upload=False, and download=False, returning empty data_path

This should be an issue of fundamentals

[larsoner]

Do you need to update sample or testing? Something like this should work

mne.datasets.sample.data_path(force_update=True, download=True, verbose=True)

[maldil]

I was trying to run following test cases.

1. https://github.com/mne-tools/mne-python/blob/6c43b2d398780e2e69ea2f5b2e3db6b59135825c/mne/preprocessing/tests/test_ica.py#L598
2. https://github.com/mne-tools/mne-python/blob/6c43b2d398780e2e69ea2f5b2e3db6b59135825c/mne/inverse_sparse/tests/test_gamma_map.py#L57
3. https://github.com/mne-tools/mne-python/blob/6c43b2d398780e2e69ea2f5b2e3db6b59135825c/mne/decoding/tests/test_csp.py#L89

So that I can an idea about the matrix sizes and shapes in the changed methods. I changed the hyper parameters to download the data as @larsoner suggested above but still no luck. Now I am dealing with below error. I would appreciate it if someone who has previously set up the project could run these and comment on the sizes and shapes. Once I know the sizes and shapes, I am happy to do a speed test.

Thank you.

0.00B [00:00, ?B/s]
Untarring contents of '/Users/root/mne_data/mne-testing-data-0.137.tar.gz' to '/Users/root/mne_data'
ERROR: usage: _jb_pytest_runner.py [options] [file_or_dir] [file_or_dir] [...]
_jb_pytest_runner.py: error: unrecognized arguments: --cov-report=
  inifile: /Users/root/Downloads/mne-python/setup.cfg
  rootdir: /Users/root/Downloads/mne-python```

[larsoner]

You need to pip install pytest-cov or conda install pytest-cov

[maldil]

Thank you for the help @larsoner This PR has an effect on five code locations (np.dots), which are shown below. I ran a test case for each of the five cases listed below to gain a better understanding of matrix shapes. Then, for each identified shape, I ran an experiment to see how multi_dot and dot perform. Below is the script that used for the experiment

from numpy import dot
from numpy.linalg import multi_dot
A = np.random.rand(38, 38)
B = np.random.rand( 38,38)
C = np.random.rand(38, 123)
%timeit -n 10 multi_dot([A, B, C])
%timeit -n 10 dot(dot(A, B), C)

Results

1. https://github.com/mne-tools/mne-python/blob/4351e611364be97c9bd156535ba73735bf6ea78d/mne/decoding/csp.py#L549 matrix shapes : cov = (4,4) , eigen_vectors[:, jj].T = (1,4) , eigen_vectors[:, jj] = (4,1) performance of multi_dot : 9.18 µs ± 4.15 µs per loop (mean ± std. dev. of 7 runs, 100 loops each) performance of dots : 17.8 µs ± 15.9 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

2. https://github.com/mne-tools/mne-python/blob/4351e611364be97c9bd156535ba73735bf6ea78d/mne/inverse_sparse/_gamma_map.py#L104 matrix shapes : U / (S + eps) : (58, 58) U.T = (58, 58) G = (58,23784) performance of multi_dot : 2.65 ms ± 79.2 µs per loop (mean ± std. dev. of 7 runs, 100 loops each) performance of dots : 2.91 ms ± 530 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

3. https://github.com/mne-tools/mne-python/blob/4351e611364be97c9bd156535ba73735bf6ea78d/mne/decoding/csp.py#L563 matrix shapes : eigen_vectors[:, ii].T = (1,4) mean_cov = (4,4) eigen_vectors[:, ii].T = (4,1) performance of multi_dot : 9.18 µs ± 4.15 µs per loop (mean ± std. dev. of 7 runs, 100 loops each) performance of dots : 17.8 µs ± 15.9 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

4. https://github.com/mne-tools/mne-python/blob/4351e611364be97c9bd156535ba73735bf6ea78d/mne/inverse_sparse/mxne_debiasing.py#L45 matrix shapes : ATA=(4,4), B=(4,4), CCT=(4,4) performance of multi_dot : 17.9 µs ± 7.38 µs per loop (mean ± std. dev. of 7 runs, 100 loops each) performance of dots : 10 µs ± 21.6 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

5. https://github.com/mne-tools/mne-python/blob/4351e611364be97c9bd156535ba73735bf6ea78d/mne/preprocessing/ica.py#L902 matrix shapes : self.unmixing_matrix_ = (38,38), self.pca_components_[:self.n_components_] = (38,38), data= (38,123) performance of multi_dot : 35.6 µs ± 5.45 µs per loop (mean ± std. dev. of 7 runs, 100 loops each) performance of dots : 44.8 µs ± 32.4 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

The results above show that multi_dot performs well, with the exception of the three square matrixes (In case 4).

As another point, using the np.dot is preferable if you are certain of the matrix forms and the best ordering. If you are not, it is recommended that you use multi_dot, which will select the appropriate ordering for you. The matrix shapes for the aforementioned scenarios, in my opinion, are not pre-known and are instead dependent on user inputs. For instance, the below csp.fit calls the functions in case 1 and 3.

https://github.com/mne-tools/mne-python/blob/4351e611364be97c9bd156535ba73735bf6ea78d/mne/decoding/csp.py#L149

[larsoner]

As another point, using the np.dot is preferable if you are certain of the matrix forms and the best ordering. If you are not, it is recommended that you use multi_dot, which will select the appropriate ordering for you. The matrix shapes for the aforementioned scenarios, in my opinion, are not pre-known and are instead dependent on user inputs.

Indeed for at least some of these it will depend on 1) the number of channels and 2) either the number of sources, or the number of PCA components retained. And these won't be fully caught by tests, since those often use many more channels and/or sources. But the fact that they speed up some of these already is sufficient for me at least to assume it'll generalize to the denser cases (where overhead is even less of a concern)!

My vote is to change all but case (4) to use multi_dot for now. We can look deeper, but based on the variable naming for (4) these all seem like they will be square, so for that I would just chain @ for readability.

There are probably other parts of the codebase that could benefit from this as well based on a git grep "np.\dot.*np\.dot", (which will itself only catch the instances that occur in a single line, and also won't catch any chained @ calls). But we should probably tackle those in another PR with appropriate benchmarking, too.

[cbrnr]

On my computer, multi_dot always performs worst, and @ best. In addition, @ is also best in readability, so my vote goes to replacing everything with @.

# multi_dot, dot, @
# Case 1:
11.1 µs ± 8.09 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
4.35 µs ± 2.39 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
3.37 µs ± 802 ns per loop (mean ± std. dev. of 7 runs, 10 loops each)

# Case 2:
10.6 ms ± 3.79 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
6.06 ms ± 1.42 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
3.91 ms ± 1.02 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

# Case 3:
12.6 µs ± 4.08 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
3.39 µs ± 1.35 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
3.26 µs ± 730 ns per loop (mean ± std. dev. of 7 runs, 10 loops each)

# Case 4:
9.9 µs ± 3.01 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
6.31 µs ± 6.51 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
3.6 µs ± 800 ns per loop (mean ± std. dev. of 7 runs, 10 loops each)

# Case 5:
40.5 µs ± 6.25 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
30.9 µs ± 642 ns per loop (mean ± std. dev. of 7 runs, 10 loops each)
30.4 µs ± 1.03 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

from timeit import timeit

import numpy as np
import pandas as pd
from numpy import dot  # noqa
from numpy.linalg import multi_dot  # noqa

shapes = [
    [(4, 4), (4, 1), (1, 4)],
    [(58, 58), (58, 58), (58, 23784)],
    [(1, 4), (4, 4), (4, 1)],
    [(4, 4), (4, 4), (4, 4)],
    [(38, 38), (38, 38), (38, 123)],
]

df = pd.DataFrame({
    "multi_dot": np.zeros(len(shapes)),
    "dot": np.zeros(len(shapes)),
    "@": np.zeros(len(shapes)),
})
for i, (r, s, t) in enumerate(shapes):
    A = np.random.rand(*r)
    B = np.random.rand(*s)
    C = np.random.rand(*t)
    t1 = timeit("multi_dot([A, B, C])", number=10, globals=globals())
    t2 = timeit("dot(dot(A, B), C)", number=10, globals=globals())
    t3 = timeit("A @ B @ C", number=10, globals=globals())
    df.iloc[i] = [t1, t2, t3]

df["shapes"] = shapes
df.set_index("shapes", inplace=True)
print(df)

[hoechenberger]

@cbrnr

On my computer, multi_dot always performs worst, and @ best. In addition, @ is also best in readability, so my vote goes to replacing everything with @.

On my M1 machine, using your benchmark code, multi_dot is always the slowest, and @ is sometimes slightly slower than dot, but probably not so much as to warrant the bad readability in comparison to @

[cbrnr]

OT: I'm a bit disappointed. Your M1 is only about 2x faster than my 8 year old MacBook Pro:

                                   multi_dot       dot         @
shapes                                                          
[(4, 4), (4, 1), (1, 4)]            0.000356  0.000034  0.000073
[(58, 58), (58, 58), (58, 23784)]   0.082977  0.067537  0.042829
[(1, 4), (4, 4), (4, 1)]            0.000283  0.000062  0.000097
[(4, 4), (4, 4), (4, 4)]            0.000197  0.000061  0.000052
[(38, 38), (38, 38), (38, 123)]     0.000381  0.000306  0.000320

But yes, I'd say we go for @ here.

[hoechenberger]

I'm a bit disappointed. Your M1 is only about 2x faster than my 8 year old MacBook Pro:

I have the slowest M1 and tried this while running on battery and with OpenBLAS. I believe there's lots of room for improvement. Besides .... pretty synthetic benchmark 😆

[cbrnr]

With everything I've read about the M1, it should not throttle at all while on battery, and even the slowest one should be much faster than an 8 year old Intel chip. And yes, these are pretty synthetic and specialized benchmarks, but it still surprised me that the difference is so small. Maybe we have to try with much larger matrices. Or there might be something wrong with your Python setup (OpenBLAS is normally very fast, comparable to Accelerate).

[drammock]

Using @cbrnr's script, but changing number from 10 to 100, I get this:

                                   multi_dot       dot         @
shapes                                                          
[(4, 4), (4, 1), (1, 4)]            0.000599  0.000166  0.000178
[(58, 58), (58, 58), (58, 23784)]   0.221222  0.189372  0.164674
[(1, 4), (4, 4), (4, 1)]            0.000582  0.000242  0.000281
[(4, 4), (4, 4), (4, 4)]            0.000611  0.000272  0.000320
[(38, 38), (38, 38), (38, 123)]     0.003133  0.002683  0.002686

So on my system too, multi_dot is slowest in every case. 🤔

[cbrnr]

Maybe something to report upstream? I thought the only reason why multi_dot exists is because it is faster...

[drammock]

Maybe something to report upstream? I thought the only reason why multi_dot exists is because it is faster...

I don't think so. I think it's faster if you're careless about putting in parentheses where it's sensible to do so. None of these test cases involve multiplication where the shapes would cause temporary creation of an intermediate larger matrix, or where the largest matrix is multiplied first (rather than last). Changing the order of parentheses like

t2 = timeit("dot(A, dot(B, C))", number=n, globals=globals())
t3 = timeit("A @ (B @ C)", number=n, globals=globals())

does indeed make dot and @ much slower than multidot for such cases:

                                   multi_dot       dot         @
shapes                                                          
[(58, 58), (58, 58), (58, 23784)]   0.233216  0.711049  1.747860

So for me, multi_dot works as expected but is not too useful for the kinds of operations we do... sure, we don't always know the dimensions in advance, but in an N×M @ M×M @ M×P operation we usually know that, for example, N << M, which is often enough info to place the parentheses optimally.

[larsoner]

we don't always know the dimensions in advance, but in an N×M @ M×M @ M×P operation we usually know that, for example, N << M, which is often enough info to place the parentheses optimally.

I agree with this in general. I'd say let's

1. transition to preferring @ instead of np.dot in new code, and when we touch old code
2. use multi_dot for cases where the shapes are variable enough (in the right ways) to benefit from it choosing the optimal order for us

And for (2) I don't think we've seen a compelling case for it yet. So my vote would be to close this PR at the moment. WDYT @maldil are you convinced?

[cbrnr]

Just a quick final question: what is the optimal order? Why do large matrices have to come last and what makes this faster than any other order?

[larsoner]

It's not really large vs small, it's tall vs short. If everything is square it doesn't matter.

Imagine an operation of the following, using shapes in place of var names: (4, 1) @ (1, 4) @ (4, 4). If the order of operations is:

1. ((4, 1) @ (1, 4)) @ (4, 4): evaluating the first/left requires 16 multiplications to get to the next operation (4, 4) @ (4, 4), and this requires 64 multiplications to get to the final output of shape (4, 4), for a total of 80 multiplies
2. (4, 1) @ ((1, 4) @ (4, 4)) evaluating the first/right requires 16 multiplications to get to the next operation (4, 1) @ (1, 4), and this requires 16 operations to get to the final output of shape (4, 4), for a total of 32 total multiplies

Here we're just talking about multiplies but the additions required are similar IIRC