parcellation_fragmenter
 parcellation_fragmenter copied to clipboard
parcellation_fragmenter copied to clipboard
Annotation restricted fragmentation
The current version takes either the whole surface or a specified region of interest (ROI) and fragments it into N-equal sized parcels.
One possible additional feature could be that the fragmentation is restricted within each annotation region. This most likely would imply that one specifies the average region size (or total number of fragments on the sphere) and that the algorithm than computes for each region, into how many parcels it would need to be fragmented.
This has been fixed -- Fragment.fit() now has a 'size' parameter, which, if specified, overrides the n_clusters parameter. If size is specified, we determine how many clusters to generate with the following check:
Fragment.fit(vertices, faces, n_clusters=n... size=s)
...
...
...
if size:
n_clusters = np.floor(n_samples / size)
which is applied either at the whole surface level, or on a region-by-region basis.
Thank you for implementing this. But am I correct that size like this means the number of vertices per ROI, not how big the surface area of the ROI should be, correct?
Yeah that's correct -- should we implement surface area? We'll need some more inputs for this -- namely how far apart in real-world space vertices are.
My thought is, if you can also fragment by surface area, that would allow that all patches in the end have kind of the same size, but are restricted by the surface parcellation. I think on the sphere, this approach is rather simple, but don't know how this can be quickly done on a folded mesh. The only open question that I have is, how can you quickly compute the area of each ROI in a parcellation "atlas"/"mask".
We could compute the surface area of a region by computing the surface area of each face in the region, using the 3D vertex coordinates of the faces.
This yes! But does that run quickly enought? Perhaps it can be optimized with cython or numba? Would be very curious to see how this works.
Hey guys! Glad I ran into this, this will be very useful. For my own research, I had done something similar in Matlab and was planning to port it to python at some point ;)
One easier approach to consider is to use the number of vertices (easy to compute for each ROI) as a proxy to its surface area (its not a bad proxy for Freesurfer, given the vertex density is pretty high). Also, there isn't usually a good justification area specifications in physical units, although if its possible, it would be good to have.
I will try to contribute if and when I can. Some sort of notes on how you envision it to be used would make it faster for me to get started.
My use case: this pkg would serve graynet: https://github.com/raamana/graynet
Hi @raamana - Great! We're very happy if you can use it for your work. And the proxy via number of vertices is a very good idea. Especially as it's quickly computed.
The vision for the implementation is probably that the user just has to specify how many parcels on the sphere he wants. With the total number of vertices on the sphere and the number of vertices per ROI, it should be a quick calculation to know how many times a specific region need to be subdivided. That's at least my vision.
What would you imagine/prefer?
Hi @raamana thanks for the feedback! Adding a parcel size option is a good idea -- the Fragment.fit() method actually has a parameter called "size" that allows for control over how many vertices large each new fragment should be, on a region-by-region basis -- if specified, "size" overrides "n_clusters" defined in the Fragment object instantiation. Though we weren't sure if we should take in a parameter describing surface area in mm^{2} or just the number of vertices per parcel....
Wouldn't the surface area of each face be homogeneous for a particular mesh? If so, the area should just be calculated on a single face and divide that from the desired surface area to get the number of vertices to apply per ROI, right? Even if they are not all the same area, the differences would be negligible for parcellations with a moderate amount of clusters.
@ctoroserey - Not sure what you mean by that. The surface of a face is not homogeneous, as it depends on the curvature it tries to model, for example:
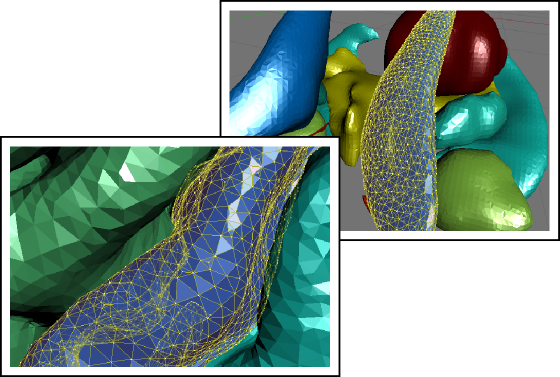
I appologize if I misunderstand what you said.
By the way, FreeSurfer has an algorithm that can computed the actual surface area of every ROI (mri_segstats), but I think the reason why it's very quick is because it's written in C.
Ah I see @miykael , thanks. So then can we just use mri_segstats? Alternatively, I still think that we would not have to calculate every face's area. We could just sample the surface and calculate the average area of the sampled faces. As @raamana said, vertex density tends to be high and I doubt that the differences in size of the faces will contribute to much variability of the total area of the ROI (in mm) (I could be completely wrong about this, but I'm trying to think of ways to avoid calculating the area of each face).
To use mri_segstats we would need the user to have FreeSurfer which is just too big of a beast as a requirements for this.
I think the average surface of a few sampled vertices could work. But in the end the question is, how accurate does the "equal size" between parcels need to be?
Anyhow, I'm happy if you want to implement both, or otherwise open a new issue for that :-)