meshzoo

When generating meshes for FEM/FVM computations, sometimes your geometry is so simple that you don't need a complex mesh generator (like pygmsh, MeshPy, mshr, pygalmesh, dmsh), but something simple and fast that makes use of the structure of the domain. Enter meshzoo.

Examples

Triangle

import meshzoo

bary, cells = meshzoo.triangle(8)

# corners = numpy.array(
#     [
#         [0.0, -0.5 * numpy.sqrt(3.0), +0.5 * numpy.sqrt(3.0)],
#         [1.0, -0.5, -0.5],
#     ]
# )
# points = numpy.dot(corners, bary).T

# Process the mesh, e.g., write it to a file using meshio
# meshio.write_points_cells("triangle.vtk", points, {"triangle": cells})

Rectangle

import meshzoo
import numpy as np

points, cells = meshzoo.rectangle_tri(
    np.linspace(0.0, 1.0, 11),
    np.linspace(0.0, 1.0, 11),
    variant="zigzag",  # or "up", "down", "center"
)

points, cells = meshzoo.rectangle_quad(
    np.linspace(0.0, 1.0, 11),
    np.linspace(0.0, 1.0, 11),
    cell_type="quad4",  # or "quad8", "quad9"
)

Regular polygon

meshzoo.ngon(4, 8)	meshzoo.ngon(6, 8)	meshzoo.ngon(9, 8)

import meshzoo

points, cells = meshzoo.ngon(5, 11)

Disk

meshzoo.disk(4, 8)	meshzoo.disk(6, 8)	meshzoo.disk(9, 8)

The disk meshes are inflations of regular polygons.

import meshzoo

points, cells = meshzoo.disk(6, 11)

points, cells = meshzoo.disk_quad(10, cell_type="quad4")  # or "quad8", "quad9"

Möbius strip

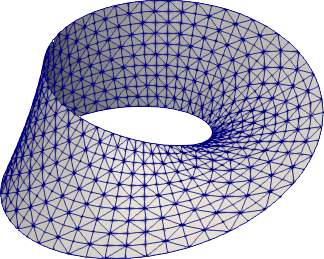
import meshzoo

points, cells = meshzoo.moebius(num_twists=1, nl=60, nw=11)

Sphere (surface)

import meshzoo

points, cells = meshzoo.uv_sphere(num_points_per_circle=20, num_circles=10, radius=1.0)
points, tri, quad = meshzoo.geo_sphere(
    num_points_per_circle=20, num_circles=10, radius=1.0
)

Spheres can also be generated by refining the faces of platonic solids and then "inflating" them. meshzoo implements a few of them. The sphere generated from the icosahedron has the highest-quality (most equilateral) triangles.

All cells are oriented such that its normals point outwards.

meshzoo.tetra_sphere(10)	meshzoo.octa_sphere(10)	meshzoo.icosa_sphere(10)

Ball (solid)

import meshzoo

points, cells = meshzoo.ball_tetra(10)
points, cells = meshzoo.ball_hexa(10)

Tube

import meshzoo

points, cells = meshzoo.tube(length=1.0, radius=1.0, n=30)

Cube

import meshzoo
import numpy as np

points, cells = meshzoo.cube_tetra(
    np.linspace(0.0, 1.0, 11), np.linspace(0.0, 1.0, 11), np.linspace(0.0, 1.0, 11)
)
points, cells = meshzoo.cube_hexa(
    np.linspace(0.0, 1.0, 11), np.linspace(0.0, 1.0, 11), np.linspace(0.0, 1.0, 11)
)