回顾基本数据结构

[ozil-110]

线性表

线性表是最简单、最常用的一种数据结构，它是n个数据元素的有限集合。实现线性表一般有数组和链表两种方式，数组用一组连续的存储单元依次存储线性表的数据元素，链表用一组任意的存储单元存储线性表的数据元素（存储单元可连续也可不连续）。

1. 数组

数组是一种大小固定的数据结构，当数组不能再存储线性表中的新元素时，我们可以创建一个新的大的数组来替换当前数组，这样就可以使用数组实现动态的数据结构。前面基于静态类型的语言，动态类型的语言，如javascript，就不同。二分查找的例子：

// 二分查找数组中的数，适用于不经常变动而查找频繁的有序列表
function binarySearch(data, arr, start, end) {
           if (start > end) {
                return -1;
            }
            var mid = Math.floor((end + start) / 2);
            if (data == arr[mid]) {
                return mid;
            } else if (data < arr[mid]) {
                return binarySearch(data, arr, start, mid - 1);
            } else {
                return binarySearch(data, arr, mid + 1, end);
            }
        }

二分查找的时间复杂度为O(logn)，比顺序查找的链表(O(n))更快，但插入、删除效率低。

2. 链表

链表是一种物理存储单元上非连续、非顺序的存储结构，逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列节点组成，这些节点不必在内存中相连。每个节点由数据部分Data和链部分Next，Next指向下一个节点，添加或者删除时，只需要改变相关节点的Next的指向，效率很高。

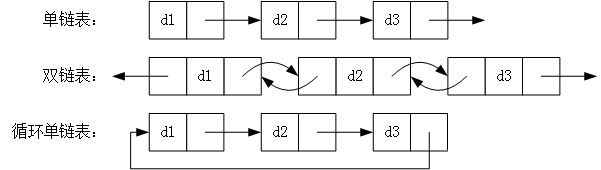
// 删除节点
var deleteNode = function (head, node) {
      // 当前节点是不是尾节点
      if (node.next) {
        node.val = node.next.val;
        node.next = node.next.next;
      // 当前只有一个节点
      } else if (node === head) {
        node = null;
        head = null;
      } else {
        // 删除的是尾节点  
        node = head;
        while (node.next.next) {
          node = node.next;
        }
        node.next = null;
        node = null;
      }
      return node;
    };
// 删除重复节点   
function deleteDuplication(pHead) {
      const map = {};
      if (pHead && pHead.next) {
        let current = pHead;
        // 计数
        while (current) {
          const val = map[current.val];
          map[current.val] = val ? val + 1 : 1;
          current = current.next;
        }
        current = pHead;
        while (current) {
          const val = map[current.val];
          if (val > 1) {
            // 删除节点
            console.log(val);
            if (current.next) {
              current.val = current.next.val;
              current.next = current.next.next;
            } else if (current === pHead) {
              current = null;
              pHead = null;
            } else {
              current = pHead;
              while (current.next.next) {
                current = current.next;
              }
              current.next = null;
              current = null;
            }

          } else {
            current = current.next;
          }
        }
      }
      return pHead;
    }

数组链表的区别：

• 数组在内存中连续存放，每个元素占用的空间相同，能通过下标快速访问，但删除和插入比较困难，需要移动大量元素。
• 链表在内存中不是顺序存储的，访问元素要从第一个开始，直到找到为止，但插入和删除比较高效，只需修改指针。
• 数组长度固定，不能动态增减，当数据增加时，可能超出原先定义的元素个数；当数据减少时，造成内存浪费，它从栈中分配空间，取速度比堆要快，但大小固定，自由度小。
• 链表动态分配，动态增减，方便插入和删除，它在堆中分配，自由度大，管理麻烦。
• javascript中的数组是对象，在堆中进行内存分配，并且是不连续的，类似哈希映射的方式存在。

下面是数组与链表插入操作对比：

    var arrInsert = [1, 2, 3];
    var arrSplice = [1, 2, 3];
    var arrList = new LinkedList();
    arrList.append(1);
    arrList.append(2);
    arrList.append(3);

    console.time("insert");
    for(var i = 0; i < 10000; i++) {
        arrInsert = insert(2, 5, arrInsert);
    }
    console.timeEnd("insert");
    console.log(arrInsert.length);


    console.time("splice");
    for(var j = 0; j < 10000; j++) {
        arrSplice.splice(2, 0, 5);
    }
    console.timeEnd("splice");
    console.log(arrInsert.length);


    console.time("arrList");
    for(var k = 0; k < 10000; k++) {
        arrList.insert(2, 5);
    }
    console.timeEnd("arrList");
    console.log(arrList.size());

    // 普通插入操作
    function insert(index, e, arr) {
        var curIndex = arr.length;

        while(curIndex > index) {
            arr[curIndex--] = arr[curIndex];
        }

        arr[curIndex] = e;

        return arr;
    }

    function LinkedList() {

    var Node = function(element){
        this.element = element;
        this.next = null;
    };

    var length = 0;
    var head = null;

    this.append = function(element){

        var node = new Node(element),
            current;

        if (head === null){
            head = node;
        } else {

            current = head;

            while(current.next){
                current = current.next;
            }

            current.next = node;
        }

        length++; 
    };

    // 链表插入操作
    this.insert = function(position, element){

        if (position >= 0 && position <= length){

            var node = new Node(element),
                current = head,
                previous,
                index = 0;

            if (position === 0){ 

                node.next = current;
                head = node;

            } else {
                while (index++ < position){
                    previous = current;
                    current = current.next;
                }
                node.next = current;
                previous.next = node;
            }

            length++; 

            return true;

        } else {
            return false;
        }
    };

    this.getHead = function(){
        return head;
    };

    this.size = function() {
        return length;
    };
}

运行结果：

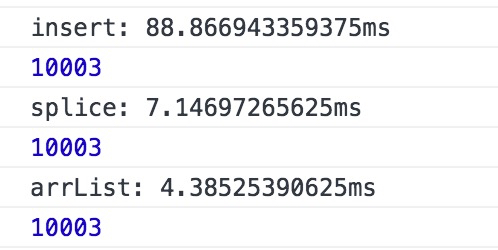
栈和队列

1. 栈

栈是一种比较特殊的线性表，访问、插入和删除元素只能在栈顶进行。

如图：

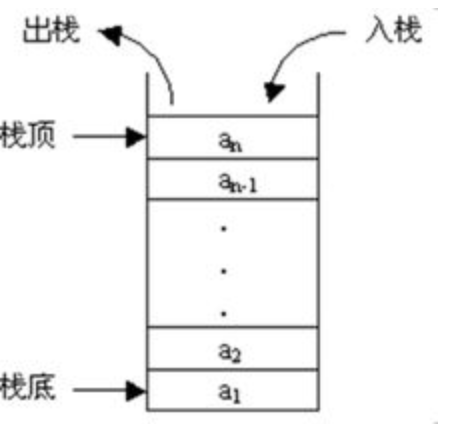
class Stack {
    constructor () {
        this.items = [];
    }
    push (element) {
        this.items.push(element);
    }
    pop () {
        return this.items.pop();
    }
    peek () {
        return this.items[this.items.length - 1];
    }
    isEmpty () {
        return this.items.length === 0;
    }
    size () {
        return this.items.length;
    }
    clear () {
        this.items = [];
    }
    print () {
        console.log(this.items.toString());
    }
}
let stack = new Stack();
console.log(stack.isEmpty());

十进制转二进制例子：

let divideBy2 = function (decNumber) {
    let remStack = new Stack();
    let rem = 0;
    let binaryString = '';
    while (decNumber > 0) {
        rem = decNumber % 2 // 记录当前余数是多少
        remStack.push(rem);  // 存入栈中
        decNumber = parseInt(decNumber / 2); // 与2除取整
    }
    while (!remStack.isEmpty()) {
        binaryString += remStack.pop().toString();
    }
    return binaryString;
};

2. 队列

队列是一种特殊的线性表，先进先出的原则，队列也有顺序队列和链式队列两种实现。数据量已知就使用数组实现队列，未知的话就使用链表实现队列。

如图：

//单链表实现
function LinkedQueue () {  
        //节点结构定义  
    var Node = function(element){  
        this.element = element;  
        this.next = null;  
    }   
  
    var length = 0,  
        front,//队首指针  
        rear;//队尾指针  
        //入队操作  
    this.push = function(element){  
        var node = new Node(element),  
            current;  
  
        if(length == 0){  
            front = node;  
            rear = node;  
            length++;  
  
            return true;  
        }else{  
            current = rear;  
            current.next = node;  
            rear = node;  
            length++;  
  
            return true;  
        }  
    }  
        //出队操作  
    this.pop = function(){  
        if(!front){  
            return 'Queue is null';  
        }else{  
            var current = front;  
            front = current.next;  
            current.next = null;  
            length--;  
            return current;  
        }  
    }  
        //获取队长  
    this.size = function(){  
        return length;  
    }  
        //获取队首  
    this.getFront = function(){  
        return front;  
    }  
        //获取队尾  
    this.getRear = function(){  
        return rear;  
    }  
        
    this.toString = function(){  
        var str = '',  
            current = front;  
  
        while(current){  
            str += current.element;  
            current = current.next;  
        }  
  
        return str;  
    }  
        //清除队列  
    this.clear = function(){  
        front = null;  
        rear = null;  
        length = 0;  
        return true;  
    }  
}

树和二叉树

树型结构是一类非常重要的非线性数据结构，二叉树是每个节点最多有两棵子树的树结构。通常子树被称作“左子树”和“右子树”。

三种遍历方式：

• 先序遍历：中左右，先找到根节点，再先序遍历左子树，再先序遍历右子树。
• 中序遍历：左中右。
• 后序遍历：左右中。

如图：

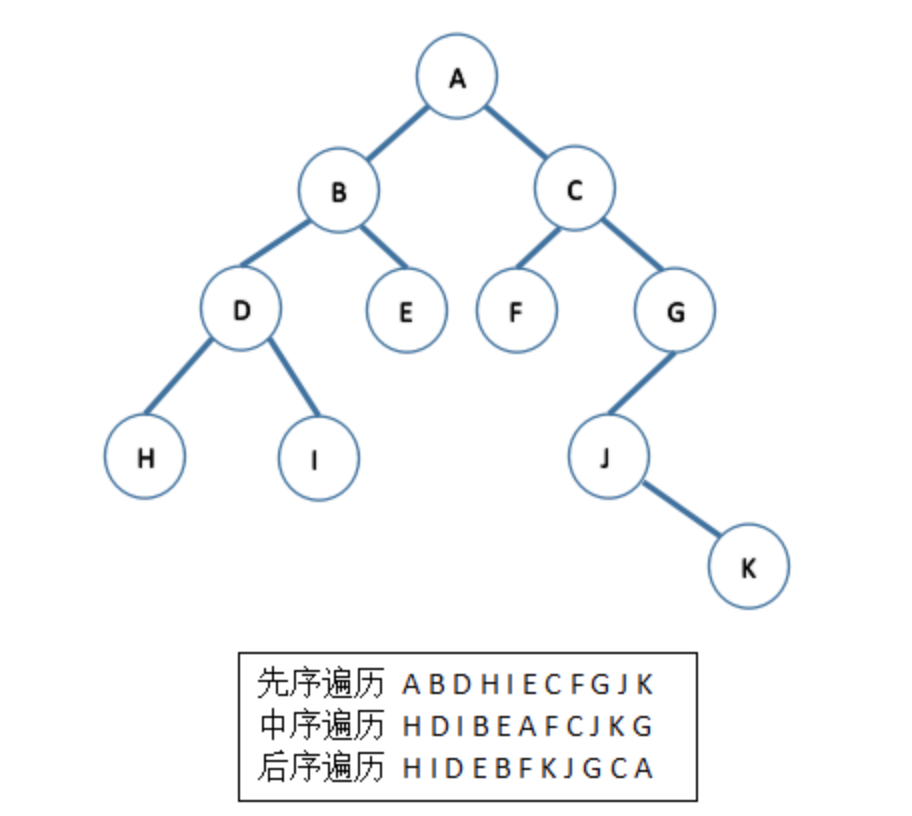
二叉搜索树的实现及遍历：

//定义节点
class Node {
    constructor(data){
        this.root = this;
        this.data = data;
        this.left = null;
        this.right = null
    }
}
//创建二叉搜索树(BST)）
class BinarySearchTree {
    constructor(){
    this.root = null
    }
    //插入节点
    insert(data){
        const newNode = new Node(data);
        const insertNode = (node,newNode) => {
            if (newNode.data < node.data){
                if(node.left === null){
                    node.left = newNode
                }else {
                    insertNode(node.left,newNode)
                }
            }else {
                if(node.right === null){
                    node.right = newNode
                }else{
                    insertNode(node.right,newNode)
                }

            }
        };
        if(!this.root){
            this.root = newNode
        }else {
            insertNode(this.root,newNode)

        }
    }
    //删除节点
    remove(data){
        const removeNode = (node,data) => {
            if(node === null) return null;
            // 找到节点
            if(node.data === data){
                // 没有左右子节点
                if(node.left === null && node.right === null) return null;
                // 没有左子节点，用右子节点覆盖
                if(node.left === null) return node.right;
                // 没有右子节点，用左子节点覆盖
                if(node.right === null) return node.left;
                // 有左右子节点，取右子树的最小节点来覆盖删除的节点并删除最小节点，而不改变树的排序
                if(node.left !==null && node.right !==null){
                let _node = this.getMin(node.right);
                node.data = _node.data;
                node.right = removeNode(node.right,_node.data);
                return node
                }
            } else if(data < node.data){
                // 递归左子树
                node.left=removeNode(node.left,data);
                return node
            } else {
                // 递归右子树
                node.right=removeNode(node.right,data);
                return node
            }
        };
        return removeNode(this.root,data)
    }
    //中序遍历
    inOrder(){
        let backs = [];
        const inOrderNode = (node,callback) => {
            if(node !== null){
                inOrderNode(node.left,callback);
                backs.push(callback(node.data));
                inOrderNode(node.right,callback)
            }
        };
        inOrderNode(this.root,callback);
        function callback(v){
            return v
        }
        return backs
    }
    //前序遍历
    preOrder(){
        let backs = [];
        const preOrderNode = (node,callback) => {
            if(node !== null){
                backs.push(callback(node.data));
                preOrderNode(node.left,callback);
                preOrderNode(node.right,callback)
            }
        };
        preOrderNode(this.root,callback);
        function callback(v){
            return v
        }
        return backs
    }
    //后序遍历
    postOrder(){
        let backs = [];
        const postOrderNode = (node,callback) => {
            if(node !== null){
                postOrderNode(node.left,callback);
                postOrderNode(node.right,callback);
                backs.push(callback(node.data))
            }
        };
        postOrderNode(this.root,callback);
        function callback(v){
            return v
        }
        return backs
    }
}

数组、链表和二叉树的比较：

操作	数组	链表	二叉树
插入、删除	O(n)	O(1)	O(logn)
查找	O(1)	O(n)	O(logn)

堆

堆就是用数组实现的二叉树，所有它没有使用父指针或者子指针，分为最大堆和最小堆。

堆的特点：

• 设父节点的编号为 i, 则其左孩子节点的编号为2i+1, 右孩子节点的编号为2i+2。
• 设孩子节点的编号为i, 则其父节点的编号为(i-1)/2。

堆与树的区别：

• 节点顺序不同。
• 内存占用不同，堆只需要一个数组来存储数据，树还需要为左右子节点分配内存。
• 平衡，二叉搜索树必须是“平衡”的情况下，复杂度为O(logn)；
• 堆中搜索会很慢。

例子： 例如数组[10, 7, 2, 5, 1]

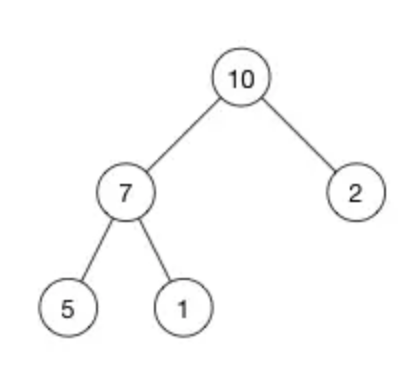
堆的实现：

function MaxHeap(initDataArray, maxSize = 9999) {
    let arr=initDataArray || [];

    let currSize=arr.length;
    // 填充heap，目前还不是一个堆
    let heap=new Array(arr.length);

    function init() {

        for(let i=0; i<currSize;i++){
            heap[i]=arr[i];
        }
        // 最后一个分支节点的父节点
        le currPos=Math.floor((currSize-2)/2);
        while (currPos>=0){
	    // 局部自上向下下滑调整
            shif_down(currPos, currSize-1);
            // 调整下一个分支节点
            currPos--;
        }

    }

    function shif_down(start,m) {
        // 父节点
        let parentIndex=start,
            // 左子节点
            maxChildIndex=parentIndex*2+1;

        while (maxChildIndex<=m){
            if(maxChildIndex<m && heap[maxChildIndex]<heap[maxChildIndex+1]){
                // 一直指向最大关键码最大的那个子节点
                maxChildIndex=maxChildIndex+1;
            }
            if(heap[parentIndex]>=heap[maxChildIndex]){
                break;
            }else {
                // 交换
                let temp=heap[parentIndex];
                heap[parentIndex]=heap[maxChildIndex];
                heap[maxChildIndex]=temp;
                // 调整它的子节点
                parentIndex=maxChildIndex;
                maxChildIndex=maxChildIndex*2+1
            }
        }
    }
    /**
     * 插入一个数据
     *
     * @param {*} data 数据值
     * @returns {boolean} isSuccess 返回插入是否成功
     */
    this.insert = function (data) {
        // 如果当前大小等于最大容量
        if(currSize===maxSize){
            return false
        }

        heap[currSize]=data;
        shif_up(currSize);
        currSize++;
        return true;
    };

    function shif_up(start) {
        let childIndex=start;   //当前叶节点
        let parentIndex=Math.floor((childIndex-1)/2); //父节点

        while (childIndex>0){
            // 如果大就不交换
            if(heap[parentIndex]>=heap[childIndex]){
                break;
            }else {
                let temp=heap[parentIndex];
                heap[parentIndex]=heap[childIndex];
                heap[childIndex]=temp;
                // 调整它的父节点
                childIndex=parentIndex;
                parentIndex=Math.floor((parentIndex-1)/2);
            }
        }
    }
}

堆的应用：

• 实现优先队列。
• 在海量数据中找到topk数据，在海量的n个数据中，使用k个数据构建一个小顶堆，遍历剩下的数据，如果元素比堆顶元素大，就删除替换堆顶元素，在调整堆。

图

图由边的集合及顶点的集合组成。边是有方向的是有序图（有向图），否则就是无序图（无向图）。可以用邻接表和邻接矩阵来表示边，邻接表是一个二维数组。

如图邻接表：

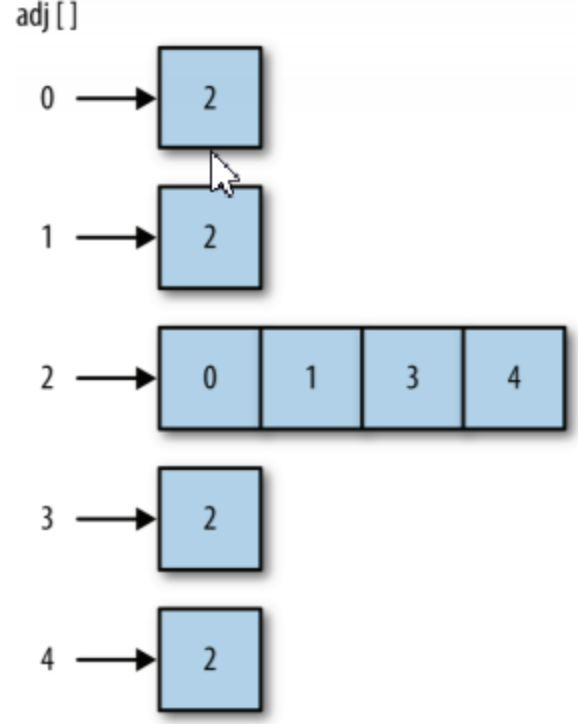
定义：

// 构造图类
function Graph(v) {
  this.vertices = v;  //顶点的数量
  this.edges = 0;
  this.adj = [];
  for (var i = 0; i < this.vertices; i++) {
    this.adj[i] = [];  //保存与顶点 i 相邻的顶点列表
  }
  this.addEdge = addEdge;
  this.showGraph = showGraph;
  this.dfs = dfs;
  this.bfs = bfs;
  this.marked = [];  //保存未访问过的顶点
  for (var i = 0; i < this.vertices; i++) {
    this.marked[i] = false;
  }
}

// 添加边
function addEdge(v, w) {
　this.adj[v].push(w);
　this.adj[w].push(v);
　this.edges++;
}

// 展示图
function showGraph() {
  for (var i = 0; i < this.vertices; i++) {
    var str = '';
    str += i + " -> ";
    for (var j = 0; j < this.vertices; j++) {
      if (this.adj[i][j] != undefined) {
        str += this.adj[i][j] + ' ';
      }
    }
    console.log(str);
  }
}

// 深度优先算法
function dfs(v) {
  this.marked[v] = true;
  if (this.adj[v] != undefined) {
    console.log("Visited vertex: " + v);
  }
  for(var w of this.adj[v]) {
    if (!this.marked[w]) {
      this.dfs(w);
    }
  }
}

// 广度优先算法
function bfs(s) {
  var queue = [];
  this.marked[s] = true;
  queue.push(s); // 添加到队尾
  while (queue.length > 0) {
    var v = queue.shift(); // 从队首移除
    if (v != undefined) {
      console.log("Visisted vertex: " + v);
    }
    for(var w of this.adj[v]) {
      if (!this.marked[w]) {this.marked[w] = true;
        queue.push(w);
      }
    }
  }
}

// 调用
g = new Graph(5);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 4);
g.showGraph();
g.dfs(0);

基本数据结构比较