x^(1/3) Not good

[APCAPCAPC]

I was working and when playing with some settings i noticed that when i tried to graph x^(1/3) it didn't draw it properly, as it showed the positive side, but on the negative side nothing was drawn. Here its the configuration

{
    "data": [
        {
            "fn": "x^(1/3)",
            "nSamples": 16000,
            "graphType": "polyline"
        }
    ],
    "xAxis": {
        "domain": [
            -7,
            7
        ]
    }
}

This is how it should be: 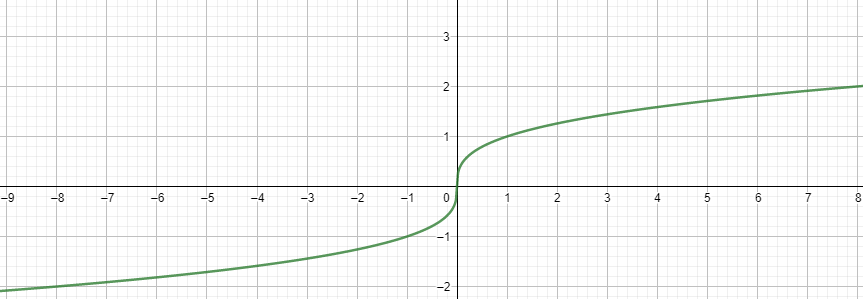And this is what the programm graphed (Note that the straight line and the text where other things not related):

[mauriciopoppe]

Thanks for the bug report! The problem is in the native Math.pow function which returns NaN if the base is negative and the exponent is a float number.

To correctly evaluate an expression like there are a few options:

• analyze the arguments in the pow nodes (somehow find out from the inner AST nodes that we have an odd/even root)
• do an approximation

Going for the approximation seems reasonable but it's not trivial to implement:

• I read https://martin.ankerl.com/2007/10/04/optimized-pow-approximation-for-java-and-c-c/ and something in JS similar could be done with https://stackoverflow.com/questions/21280440/converting-two-uint32array-values-to-javascript-number/21282715#21282715

[mauriciopoppe]

I tried a few examples of https://martin.ankerl.com/2007/10/04/optimized-pow-approximation-for-java-and-c-c/ and the results were far from good:

• 3^3=26.217211
• 2^10=994.312012

[APCAPCAPC]

I have an idea, but i do not know how to implement it. So, having in mind that it calculates the values correctly when the input is positive, we could do something like this:

Explanation:

• |x| means the absolute value of x, basicly if Enters: positive Out: positive Enters: negative Out: positive
• sign(x) means the sign that has x. For instance, if x is -14, then sign(x) is -1. Like is only the sign. What all of this is doing is converting the input to positive, calculate the ^(1/3), and then aplying the sign.

Hope this helps.

[mauriciopoppe]

Thanks for the suggestion, I think that the formula depends on the exponent denominator, let's take two examples:

• $x^\frac{1}{2} = \sqrt{x}$ and this is only defined for $x \geq 0$, this happens for every even denominator
• $x^\frac{1}{3} = \sqrt[3]{x}$, it's defined for any rational number $x$, this happens for every odd denominator

As you can see it's a matter of analyzing the denominator if the power is a fraction

[minhhai2209]

The definition of the power function $a^x$ requires that $a$ is positive. I don't think this is a bug. The current plot is correct.

Edit: If you want the first plot it should be the function $\sqrt[3]{x}$.

Edit: @mauriciopoppe That means if this is "fixed" then the fix would actually be a bug. Thank you so much for this great library btw!

[APCAPCAPC]

@minhhai2209 That is a false argument. I will use this as an example: 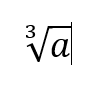What this expression does, is search a number, that multiplied by itself 3 times equals to a. Thus, it does not need to always be positive. Lets say that we are finding: 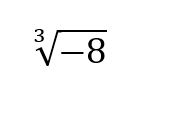If the 8 was positive, the solution would be 2, as (2)(2)(2) = 8. But, we have a negative number. However we can get negative numbers as a result: (-2)(-2)(-2) = -8. This happens because it isn't an even number of multiplications, so the negative signs don't cancel each other out. And how this all relates to exponents, roots are a representation of exponentials: 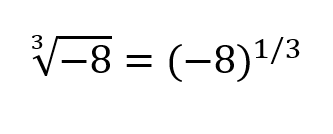Thus, in conclusion, what you said, that it needs to be positive, will only be true when the denominator of the exponential is even.

[APCAPCAPC]

@mauriciopoppe I agree on what you said. So, to solve the problem, we would need to know if the denominator is odd in order to apply the formula i mentioned a few comments ago?

I will change prespective, as I find easier to work with even numbers. So, what we can do is exactly the opposite: See only if it's even and not apply the formula.

So we are searching numbers that fall in these two categories:

• It has to be even
• It does not have any decimal digits

we could identify any even number just dividing by 2, and if we get a result that has no decimals, it would be an even, and the solution wouldn't be applied. In any other case, that it isn't even, we would apply the solution.

As I said in my other comment, i do not know what tools are available in your framework to make this work. So I don't know how would you implement such a thing. Hope everything helps.

[minhhai2209]

@APCAPCAPC Per the formal definition the function $a^{1/3}$ is different from the function $\sqrt[3]{a}$. What you have written 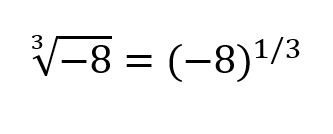is simply wrong.

More discussion here https://www.researchgate.net/publication/226461615_To_define_or_not_to_define_The_case_of_-813.

The solution to ${-8}^{1/3}$ can only be possible using complex numbers.

@minhhai2209 That is a false argument. I will use this as an example: What this expression does, is search a number, that multiplied by itself 3 times equals to a. Thus, it does not need to always be positive. Lets say that we are finding: If the 8 was positive, the solution would be 2, as (2)(2)(2) = 8. But, we have a negative number. However we can get negative numbers as a result: (-2)(-2)(-2) = -8. This happens because it isn't an even number of multiplications, so the negative signs don't cancel each other out. And how this all relates to exponents, roots are a representation of exponentials: Thus, in conclusion, what you said, that it needs to be positive, will only be true when the denominator of the exponential is even.

[APCAPCAPC]

@minhhai2209 I see the problem now. Thanks for referencing that paper, it helped a lot. So, this sort of reminds me of Because it has two solutions, -1, +1, we take the positive one. And I think we could do something similar here.

I'm still having a mental debate between the two solutions, as for me both make some sense. I would like to hear what do you think

[stale[bot]]

This issue has been automatically marked as stale because it has not had recent activity. It will be closed if no further activity occurs. Thank you for your contributions.

[stale[bot]]

This issue has been automatically marked as stale because it has not had recent activity. It will be closed if no further activity occurs. Thank you for your contributions.

[manstie]

Could you find all the roots then take the non-complex result?

[stale[bot]]

This issue has been automatically marked as stale because it has not had recent activity. It will be closed if no further activity occurs. Thank you for your contributions.

[mauriciopoppe]

Hey guys, after so many months I remembered I already implemented this a long time ago (in 2015 https://github.com/mauriciopoppe/interval-arithmetic/commit/baf57bdce3b327a9aec4b9d5a57be50f0212dba3) 😅. While you can't use x^(1/3) you can use a function called nthRoot.

functionPlot({
  target: '#playground',
  data: [
    {
      fn: 'nthRoot(x, 3)',
    }
  ]
})

https://codesandbox.io/p/sandbox/silent-firefly-z8wjp7