I'm not sure if tf.sqrt caused the loss to be nan

[SongPapers]

Hi Dr.Lu, Thank you very much for sharing and answering. I am trying to simulate a system of equations and solve it by DeepXDE. However I meet a problem. In order to briefly, I give the picture and the code.

A set of equations are given by

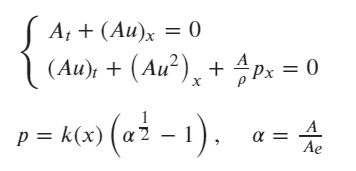
The input variables are x and t as well as the outputs are A and u. Ae = 1, k(x) = 1.

Then I set up a network.

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import deepxde as dde
from deepxde.backend import tf
import numpy as np

from matplotlib import pyplot as plt
dde.config.real.set_float64()



Ae = 1.0
k = 1
rho = 1.0 

def pde(x,f):
    A = f[:,0:1]
    u = f[:,1:2]
    
#     p = f[:,2:3]
#     eq3 = (p/k + 1 )**2 - (A/Ae)
#     eq3 = p - k*((A/Ae)**(1/2)-1)
    Au = A*u
    Au2 = A*u*u
    p = k*(tf.sqrt(A/Ae)-1)
    
    
    A_t = dde.grad.jacobian(f, x, i=0, j=1)
#     Au_x = dde.grad.jacobian(Au)
    Au_x = tf.gradients(Au, x)[0][:, 0:1]
    Au_t = tf.gradients(Au, x)[0][:, 1:2]
    Au2_x = tf.gradients(Au2, x)[0][:, 0:1]
    p_x = tf.gradients(p, x)[0][:, 0:1]
#     p_x = dde.grad.jacobian(f, x, i=2, j=0)
    
    eq1 = A_t + Au_x
    eq2 = Au_t + Au2_x + p_x*A/rho
    return [eq1, eq2]
#     return [eq1, eq2, eq3]



A_ic = 1
u_ic = 1

def on_initial(_, on_initial):
    return on_initial

def func_IC_A(x):    
    return A_ic

def func_IC_u(x):
    return u_ic

def boundary_Al(x, on_boundary):
    return on_boundary and np.isclose(x[0], 0)

def boundary_ul(x, on_boundary):
    return on_boundary and np.isclose(x[0], 0)

def boundary_Ar(x, on_boundary):
    return on_boundary and np.isclose(x[0], 1)

def boundary_ur(x, on_boundary):
    return on_boundary and np.isclose(x[0], 1)



geom = dde.geometry.Interval(0, 1)
timedomain = dde.geometry.TimeDomain(0, 1)
geomtime = dde.geometry.GeometryXTime(geom, timedomain)


IC_A = dde.IC(geomtime, func_IC_A, on_initial, component = 0)
IC_u = dde.IC(geomtime, func_IC_u, on_initial, component = 1)

BC_Al = dde.DirichletBC(geomtime, lambda x: 0, boundary_Al, component = 0)
BC_ul = dde.DirichletBC(geomtime, lambda x: 0, boundary_ul, component = 1)
BC_Ar = dde.DirichletBC(geomtime, lambda x: 0, boundary_Ar, component = 0)
BC_ur = dde.DirichletBC(geomtime, lambda x: 0, boundary_ur, component = 1)

data = dde.data.TimePDE(
    geomtime,
    pde,
    [IC_A, IC_u, BC_Al, BC_ul, BC_Ar, BC_ur],
    num_domain = 1000,
    num_boundary = 50,
    num_initial  = 100,
)


net = dde.maps.FNN(
    layer_sizes = [2] + [50]*5 + [2],
    activation         = "tanh",
    kernel_initializer = "Glorot uniform"
)

model = dde.Model(data, net)
model.compile('adam', 
              lr = 0.0005,
#              loss_weights=[1, 0.001, 100, 100, 100, 100]
)
model.train(epochs=1000)

But the loss function has nan cases:

Initializing variables...
Training model...

Step      Train loss                                                                          Test loss                                                                           Test metric
0         [2.12e-03, nan, 1.02e+00, 1.15e+00, 1.16e-03, 1.19e-02, 1.03e-04, 4.83e-03]         [2.12e-03, nan, 1.02e+00, 1.15e+00, 1.16e-03, 1.19e-02, 1.03e-04, 4.83e-03]         []  
1000      [nan, nan, nan, nan, nan, nan, nan, nan]                                            [nan, nan, nan, nan, nan, nan, nan, nan]                                            []  

Best model at step 0:
  train loss: inf
  test loss: inf
  test metric: 

The problem is the second loss function and the corresponding code is " eq2 = Au_t + Au2_x + p_xA/rho ". Further, the problem is " p = k(tf.sqrt(A/Ae)-1) ". I find that nan does not appear if tf.sqrt() (same as **(1/2) ) is removed.

I don't understand why? Looking forward to your answer~

[SongPapers]

PS: This problem does not occur if p is set as the output of the network ( inputs: x,t, outputs: A, u, p ).

When defining "eq3 = p - k*((A/Ae)**(1/2)-1) ", the net will work, while net cannot work if "eq3 = p - k*(tf.sqrt(A/Ae) -1) ".

[lululxvi]

You need to make sure A/Ae > 0.

[SongPapers]

You need to make sure A/Ae > 0.

Oh my God, To be so involved with the result that forget the most important details. Thx~

[tjboise]

You need to make sure A/Ae > 0.

Oh my God, To be so involved with the result that forget the most important details. Thx~

Hi, Would you like to tell me how you did in order to make sure A/Ae>0?

[SongPapers]

Hi, you could use function tf.sign to make sure A/Ae>0