[BUG] Single phase delta load modeling for LinDist3FlowPowerModel

[gbyeon]

Describe the bug It seems there might be a bug in single-phase delta load modeling for LinDist3FlowPowerModel (especially, in function function constraint_mc_load_power(pm::LPUBFDiagModel, load_id::Int; nw::Int=nw_id_default, report::Bool=true))

Minimum Viable Example The IEEE13 open dss file is used, which has two single phase delta loads: Load.646 and Load.692. I have instantiated a linear opf model using pm = instantiate_mc_model(math, LinDist3FlowPowerModel, build_mc_opf).

Expected behavior Impedance Load.646 (index 15) located at bus 646 (index 16) has only phase 2, so I expected it to add the following constraints: -0.0023000000000000013 0_w_16[2] + 0_Xdr_22[15] - 0_Xdr_32[15] = 0.0 -0.0013200000000000009 0_w_16[2] + 0_Xdi_22[15] - 0_Xdi_32[15] = 0.0 and 0_p_(6, 16, 9)[2] - 0_Xdr_21[15] + 0_Xdr_22[15] = 0.0 0_q_(6, 16, 9)[2] - 0_Xdi_21[15] + 0_Xdi_22[15] = 0.0 0_p_(6, 16, 9)[3] - 0_Xdr_32[15] + 0_Xdr_33[15] = 0.0 0_q_(6, 16, 9)[3] - 0_Xdi_32[15] + 0_Xdi_33[15] = 0.0

Screenshots However, for Load.646, it generates -0.0023000000000000013 0_w_16[2] + 0_Xdr_33[15] - 0_Xdr_13[15] = 0.0 (seems to link phase 3 to phase 2) -0.0013200000000000009 0_w_16[2] + 0_Xdi_33[15] - 0_Xdi_13[15] = 0.0 and 0_p_(6, 16, 9)[2] - 0_Xdr_32[15] + 0_Xdr_33[15] = 0.0 (seems to link phase 3 to phase 2) 0_q_(6, 16, 9)[2] - 0_Xdi_32[15] + 0_Xdi_33[15] = 0.0 0_p_(6, 16, 9)[3] - 0_Xdr_13[15] + 0_Xdr_11[15] = 0.0 (seems to link phase 1 to phase 2) 0_q_(6, 16, 9)[3] - 0_Xdi_13[15] + 0_Xdi_11[15] = 0.0

Load.692 shows a similar behavior.

System Information (please complete the following information):

• Version: v0.14.4

Additional context I might have an incorrect understanding of the meaning of Xdr and Xdi. I have summarized my understanding of the delta load model as follows; it would be very much appreciated if you could correct me or recommend a good reference if there is anything I might be wrong.

• three phase delta load:

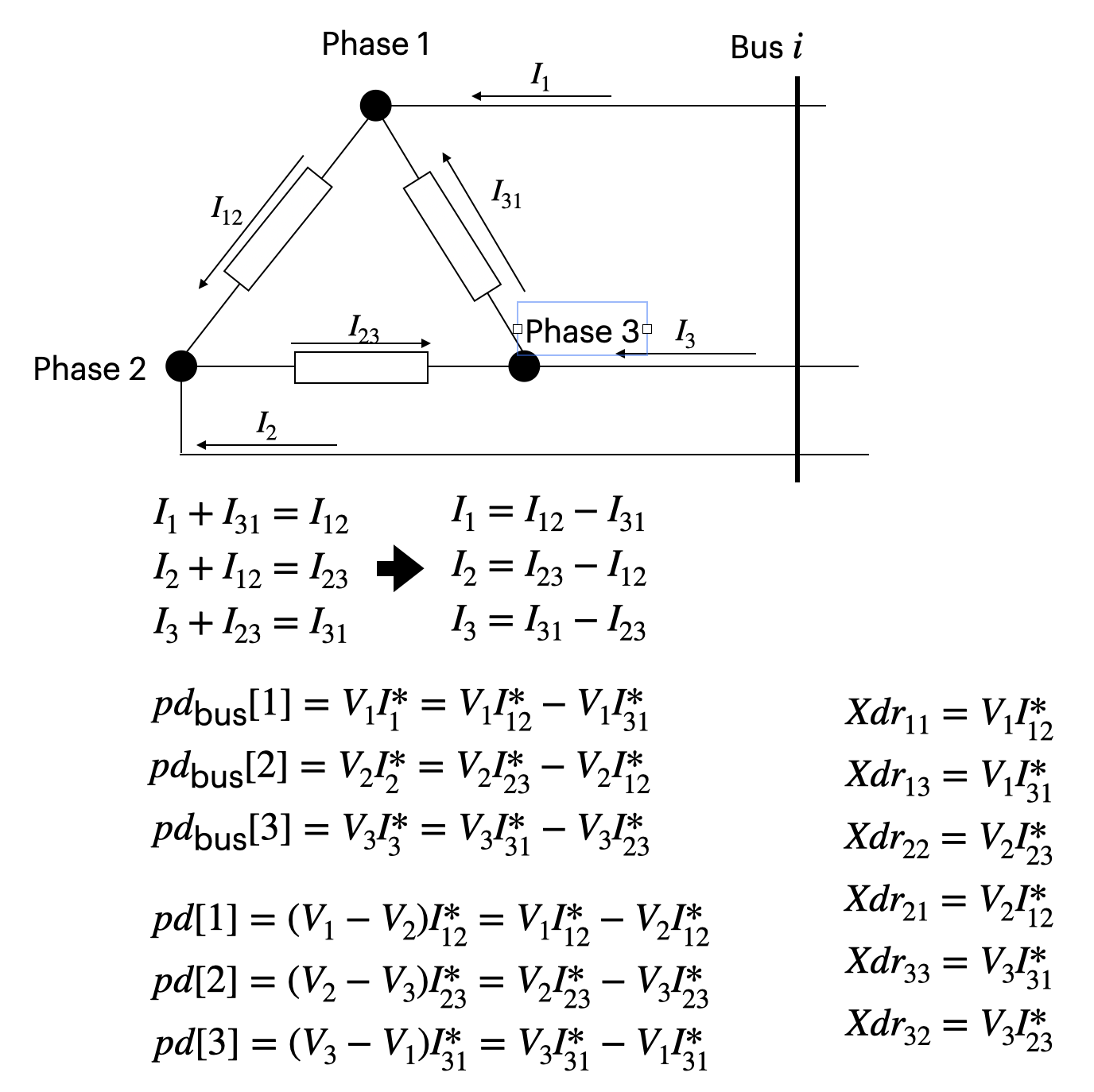
• single phase delta load of phase 2:

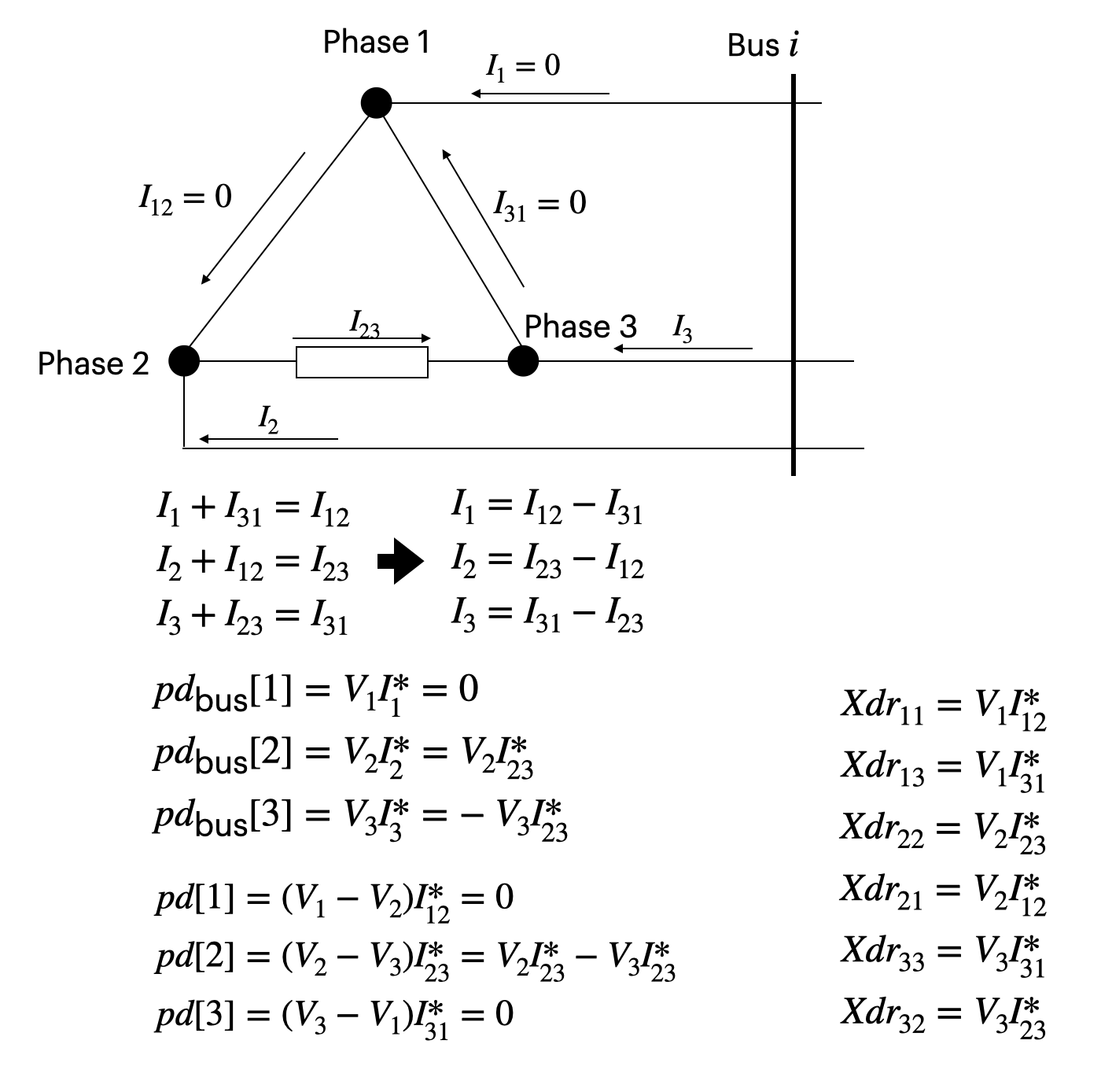
If my understanding is correct, it seems that the bug can be fixed by correctly linking indices as follows: Replace Line 429:451 in bf_mx_lin.jl with

var(pm, nw, :pd_bus)[load_id] = Array{AffExpr}(undef, 3)
        var(pm, nw, :qd_bus)[load_id] = Array{AffExpr}(undef, 3)
        var(pm, nw, :pd)[load_id] = Array{AffExpr}(undef, 3)
        var(pm, nw, :qd)[load_id] = Array{AffExpr}(undef, 3)
        for (idx, c) in enumerate(connections)
            var(pm, nw, :pd_bus)[load_id][c] = pd_bus[idx]
            var(pm, nw, :qd_bus)[load_id][c] = qd_bus[idx]
            var(pm, nw, :pd)[load_id][c] = pd[idx]
            var(pm, nw, :qd)[load_id][c] = qd[idx]
        end
        if load["model"]==POWER
            for (idx, c) in enumerate(connections)
                JuMP.@constraint(pm.model, pd[idx]==pd0[idx])
                JuMP.@constraint(pm.model, qd[idx]==qd0[idx])
            end
        elseif load["model"]==IMPEDANCE
            w = var(pm, nw, :w)[bus_id][[c for c in connections]]
            for (idx,c) in enumerate(connections)
                JuMP.@constraint(pm.model, pd[idx]==3*a[c]*w[c])
                JuMP.@constraint(pm.model, qd[idx]==3*b[c]*w[c])
            end
        else
            w = var(pm, nw, :w)[bus_id][[c for c in connections]]
            for (idx,c) in enumerate(connections)
                JuMP.@constraint(pm.model, pd[idx]==sqrt(3)/2*a[c]*(w[c]+1))
                JuMP.@constraint(pm.model, qd[idx]==sqrt(3)/2*b[c]*(w[c]+1))
            end
        end

Thank you in advance for your help!

[pseudocubic]

Thank you for the report, it is very thorough, I really appreciate it! I will review the information you provided

[gbyeon]

Thank you very much, David!

One more point: it seems that the indexing for Line 424 and Lines 436:437 may also be incorrectly linked since the phase order of pd0 and qd0 are always according to [1 2 3], not according to "connections". We may change them as: Line 424 to if abs(pd0[c]+im*qd0[c]) == 0.0 and Lines 436:437 to

JuMP.@constraint(pm.model, pd[idx]==pd0[c])
JuMP.@constraint(pm.model, qd[idx]==qd0[c])

Then, surprisingly, it gives us a very similar result as the previous implementation.

[minseok-ryu]

It seems that the new model (applying Geunyeong's input) and the original model are equivalent but using different indices. Taking the same example:

The feasible region of the ORIGINAL model:

 Xdr_22[15] = 0.0
 Xdr_32[15] = 0.0
 Xdr_12[15] = 0.0
 Xdi_22[15] = 0.0
 Xdi_32[15] = 0.0
 Xdi_12[15] = 0.0
 Xdr_21[15] = 0.0
 Xdr_31[15] = 0.0
 Xdr_11[15] = 0.0
 Xdi_21[15] = 0.0
 Xdi_31[15] = 0.0
 Xdi_11[15] = 0.0
 Xdr_22[15] - Xdr_32[15] = 0.0
 Xdi_22[15] - Xdi_32[15] = 0.0
 -0.0023000000000000013 w_16[2] + Xdr_33[15] - Xdr_13[15] = 0.0
 -0.0013200000000000009 w_16[2] + Xdi_33[15] - Xdi_13[15] = 0.0
 -Xdr_21[15] + Xdr_11[15] = 0.0
 -Xdi_21[15] + Xdi_11[15] = 0.0
 pb1[2] : -Xdr_32[15] + Xdr_33[15] + p_hat_(7, 16, 9)[2] = 0.0
 pb2[2] : -Xdi_32[15] + Xdi_33[15] + q_hat_(7, 16, 9)[2] = 0.0
 pb1[3] : -Xdr_13[15] + Xdr_11[15] + p_hat_(7, 16, 9)[3] = 0.0
 pb2[3] : -Xdi_13[15] + Xdi_11[15] + q_hat_(7, 16, 9)[3] = 0.0
 pb1[1] : Xdr_22[15] - Xdr_21[15] = 0.0
 pb2[1] : Xdi_22[15] - Xdi_21[15] = 0.0

The feasible region of the NEW model (applying Geunyeong's input)

 Xdr_23[15] = 0.0
 Xdr_33[15] = 0.0
 Xdr_13[15] = 0.0
 Xdi_23[15] = 0.0
 Xdi_33[15] = 0.0
 Xdi_13[15] = 0.0
 Xdr_21[15] = 0.0
 Xdr_31[15] = 0.0
 Xdr_11[15] = 0.0
 Xdi_21[15] = 0.0
 Xdi_31[15] = 0.0
 Xdi_11[15] = 0.0
 -0.0023000000000000013 w_16[2] + Xdr_22[15] - Xdr_32[15] = 0.0
 -0.0013200000000000009 w_16[2] + Xdi_22[15] - Xdi_32[15] = 0.0
 Xdr_33[15] - Xdr_13[15] = 0.0
 Xdi_33[15] - Xdi_13[15] = 0.0
 -Xdr_21[15] + Xdr_11[15] = 0.0
 -Xdi_21[15] + Xdi_11[15] = 0.0
 pb1[2] : Xdr_22[15] - Xdr_21[15] + p_hat_(7, 16, 9)[2] = 0.0
 pb2[2] : Xdi_22[15] - Xdi_21[15] + q_hat_(7, 16, 9)[2] = 0.0
 pb1[3] : -Xdr_32[15] + Xdr_33[15] + p_hat_(7, 16, 9)[3] = 0.0
 pb2[3] : -Xdi_32[15] + Xdi_33[15] + q_hat_(7, 16, 9)[3] = 0.0
 pb1[1] : -Xdr_13[15] + Xdr_11[15] = 0.0
 pb2[1] : -Xdi_13[15] + Xdi_11[15] = 0.0

Change the indices of "Xdr" and "Xdi" in the New Model as follows:

11 -> 22
12 -> 23
13 -> 21
21 -> 32
22 -> 33
23 -> 31
31 -> 12
32 -> 13
33 -> 11

Then we have

 Xdr_31[15] = 0.0
 Xdr_11[15] = 0.0
 Xdr_21[15] = 0.0
 Xdi_31[15] = 0.0
 Xdi_11[15] = 0.0
 Xdi_21[15] = 0.0
 Xdr_32[15] = 0.0
 Xdr_12[15] = 0.0
 Xdr_22[15] = 0.0
 Xdi_32[15] = 0.0
 Xdi_12[15] = 0.0
 Xdi_22[15] = 0.0
 -0.0023000000000000013 w_16[2] + Xdr_33[15] - Xdr_13[15] = 0.0
 -0.0013200000000000009 w_16[2] + Xdi_33[15] - Xdi_13[15] = 0.0
 Xdr_11[15] - Xdr_21[15] = 0.0
 Xdi_11[15] - Xdi_21[15] = 0.0
 -Xdr_32[15] + Xdr_22[15] = 0.0
 -Xdi_32[15] + Xdi_22[15] = 0.0
 pb1[2] : Xdr_33[15] - Xdr_32[15] + p_hat_(7, 16, 9)[2] = 0.0
 pb2[2] : Xdi_33[15] - Xdi_32[15] + q_hat_(7, 16, 9)[2] = 0.0
 pb1[3] : -Xdr_13[15] + Xdr_11[15] + p_hat_(7, 16, 9)[3] = 0.0
 pb2[3] : -Xdi_13[15] + Xdi_11[15] + q_hat_(7, 16, 9)[3] = 0.0
 pb1[1] : -Xdr_21[15] + Xdr_22[15] = 0.0
 pb2[1] : -Xdi_21[15] + Xdi_22[15] = 0.0

which is equivalent to the ORIGINAL model.