fucking-algorithm
 fucking-algorithm copied to clipboard
fucking-algorithm copied to clipboard
经典动态规划:完全背包问题 :: labuladong的算法小抄
base case代码里没写dp[0][j]的情况
Java中int数组创建后所有元素都默认是0,所以为0的base case就不需要再初始化了。 如果其他语言不是这样,还是需要代码初始化一下。
如果把 第 i 物品装入背包的情况下, dp[i][j] 不是应该等于dp[i-1][j-coins[i-1]] 吗?
大佬,想问一下,为什么进行空间优化的时候,子集背包那题,j 需要从后往前遍历,而这里不需要呢?
@NiceMartin 如果把 第 i 物品装入背包的情况下, dp[i][j] 不是应该等于dp[i-1][j-coins[i-1]] 吗?
我也这么觉得。如果你决定使用这个面值的硬币,那么就应该关注如何凑出金额 j - coins[i-1]。
比如说,你想用面值为 2 的硬币凑出金额 5,那么如果你知道了凑出金额 3 的方法,再加上一枚面额为 2 的硬币,不就可以凑出 5 了嘛。
所以先dp[i-1][j-coins[i-1]] ,再加上这个面值的硬币。组合数不变。
不过从二维优化到一维之后是一样的。
但是把dp[i][j - coins[i-1]]改成 dp[i-1][j-coins[i-1]] ,提交是错的!
如果把 第 i 物品装入背包的情况下, dp[i][j] 不是应该等于dp[i-1][j-coins[i-1]] 吗?
这里每个硬币可以选用无限多次,即物品的数量是无限的,所以第 i 个物品装入一次后还是可以继续使用的,反映到状态转移方程上是 dp[i][j-coins[i-1]]。 @Tokics @NiceMartin
大佬,想问一下,为什么进行空间优化的时候,子集背包那题,j 需要从后往前遍历,而这里不需要呢?
@tiertie 关于空间优化的问题,在网站搜索「对动态规划进行降维打击」这篇文章,有详细解释。
感谢大佬的答复,我终于明白了。我理解的是这样的:
dp[i][j]中使用 i 的次数是 [0, +∞],当不使用 i 的时候,dp[i][j]=dp[i-1][j];
所以也是只有在不使用 i 这个硬币的时候,才会 dp[i][j-coins[i-1]] = dp[i-1][j-coins[i-1]]。假设等号左边是(A),等号右边是(B),那么 B 就是 A 的子集!A 还包括了一部分 C。
——————
比如说,你想用面值为 2 的硬币凑出金额 5,那么如果你知道了凑出金额 3 的方法,再加上一枚面额为 2 的硬币,不就可以凑出 5 了嘛。
——————
回到这句话,这里 coins[i-1]就是 2, 我们想凑出 dp[i][5], 可以先凑出 dp[i][3], 这里是 i 而不是i-1, 否则就漏掉了使用 2 这个硬币组成 3 这个总金额的组合,就是我们上面说的,漏掉了 C。所以用 dp[i-1][3]是错的,漏了 C这个部分。
压缩状态是我看漏了哪一章吗大佬,有点卡不懂压缩状态
@zxcvbnmleizhe 看 这篇
将凑零钱II 和 凑零钱I 格式统一
- 效率不高 但是 格式统一后 就能顺势推导了
- 感谢 东哥的 思路引导,谢谢
public int coinChange(int[] coins, int amount) {
int[][] dp = new int[coins.length+1][amount+1];
// coin = 0 没有钱
for(int j = 1 ; j <=amount;j++){
dp[0][j] = Integer.MAX_VALUE;
}
//amount = 0 要凑的钱 为 0
for(int i = 0; i<=coins.length;i++){
dp[i][0] = 0;
}
for(int i = 1; i<=coins.length;i++){
for(int j = 1; j<=amount;j++){
//注意这里需要对 Interger.MAX_VALUE 这个边界初始值进行判断
if( j >= coins[i-1] && dp[i][j-coins[i-1]]!=Integer.MAX_VALUE ){
dp[i][j] = Math.min(dp[i-1][j],dp[i][j-coins[i-1]]+1);
}else{//面额大于 要凑的钱
dp[i][j] = dp[i-1][j];
}
}
}
return dp[coins.length][amount] == Integer.MAX_VALUE ? -1: dp[coins.length][amount];
}
}
class Solution {
// dp[i][j] 表示 将i个硬币装入背包 , 剩余 需要凑的钱(j)是多少
public int change(int amount, int[] coins) {
int[][] dp = new int[coins.length+1][amount+1];
//base case
for(int i = 0; i<= coins.length;i++){
dp[i][0] = 1;//base case 就是要凑 0 元 说明直接每种硬币都能拿到一种可能性 就是啥也不装
}
for(int i = 1; i<=coins.length; i++){
for(int j = 1;j<=amount; j++){
if(j >= coins[i-1]){//要凑的钱 比 当前的硬币面值大
int a = dp[i-1][j];//依赖于前一种 当前不拿硬币 就剩余要凑 j 了
int b = dp[i][j-coins[i-1]];//当前拿了硬币 装入硬币了 就剩余要凑 j-coins[i-1]
dp[i][j] = a+b;//因为要求的是总共多少可能 组合数 需要将两种情况的组合数相加
}else{//剩余要凑的 j 元 比 当前的硬币面值还要小 说明凑不出来 只能依赖前一种
dp[i][j] = dp[i-1][j];
}
}
}
return dp[coins.length][amount];
}
}
@zhongweiLeex 给你的思考点赞👍
@Tokics 这恰恰就是01背包和完全背包的区别 dp[i][j] = dp[i-coins[j-1]][j] +dp[i][j-1] #完全背包,可以重复使用自己 dp[i][j] = dp[i-coins[j-1]][j-1] +dp[i][j-1] #01背包,不能重复使用
@labuladong 东哥,这里有笔误哇? “如果你不把这第 i 个物品装入背包,也就是说你不使用 coins[i] (应该是coins[i-1]?)这个面值的硬币,那么凑出面额 j 的方法数 dp[i][j] 应该等于 dp[i-1][j],继承之前的结果。
如果你把这第 i 个物品装入了背包,也就是说你使用 coins[i] (应该是coins[i-1]?)这个面值的硬币,那么 dp[i][j] 应该等于 dp[i][j-coins[i-1]]。”
@lee666-lee 感谢指出,确实有笔误,已修复~
for(int i = 1; i<=n ;i++) {
for (int j =1; j<= amount; j++) {
int num = coins[i-1];
if (num > j) {
dp[i][j] = dp[i-1][j];
} else {
// dp[i][j] = dp[i-1][j] + dp[i][j-num];
int nums = 0;
int count = 0;
while(count * num < j) {
count ++;
}
for(int m = 1; m<count; m ++) {
nums += dp[i-1][j - m * num];
}
nums += dp[i-1][j];
dp[i][j] = nums;
}
}
}
return dp[n][amount];
不知道为什么这样的状态转移方程不对,感觉也考虑了所有情况,对于第i个硬币列举了所有可能性然后相加
按照东哥的思路,画了一个图,便于理解两种背包思路的区别
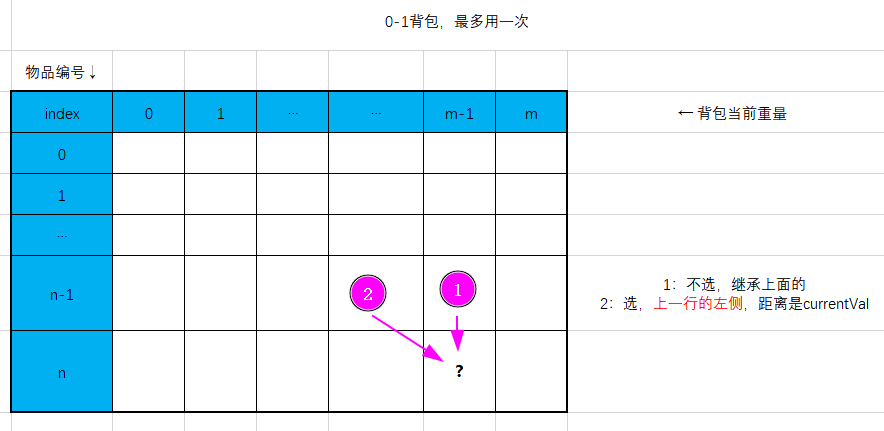
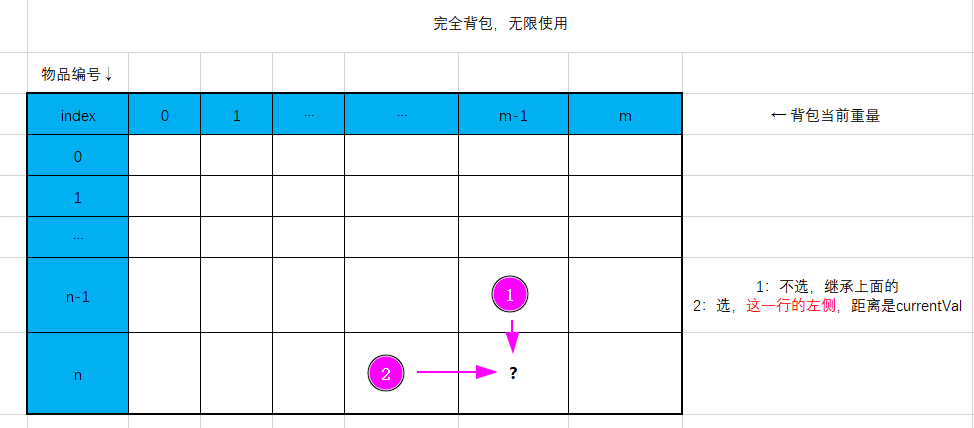
@hwhaocool 点赞!
我觉得从状态定义的有没有意义上来讲,若只使用 coins 中的前 i 个(i 从 1 开始计数)硬币的面值,若想凑出金额 j,有 dp[i][j] 种凑法。。 这种定义是有错误的,为什么不让凑金额j的时候使用coins中的i后面的值呢?
楼上,那你还用啥子问题思路呢,子问题能推出原问题就是对的
东哥,不知道我这样理解对不对呢
完全背包问题和01背包的差别:
完全背包:第i件可重复,所以是i的状态转移 dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]];
01背包:第i件物品不能重复,所以是上一个i-1的状态转移 dp[i][j] = dp[i-1][j] + dp[i-1][j-coins[i-1]];
@Maxiah 状态转移是这样的,也可以参考下 回溯算法秒杀所有排列组合子集问题 中元素可重的排列组合是怎么算的。
base case一个建议 “base case 为 dp[0][..] = 0, dp[..][0] = 1。因为如果不使用任何硬币面值,就无法凑出任何金额;如果凑出的目标金额为 0,那么“无为而治”就是唯一的一种凑法。” 这段不是很好理解,尤其是后半句dp[..][0] = 1 无为而治太抽象了 我的做法是dp[0][0]=1 其余dp[0][..] = 0 不选任何硬币当然可以凑出面值为0的方案,且只有一种,而不能凑成面值>0的方案。 而剩下的dp[..][0]交给迭代去处理不是更好吗?
int n = coins.length;
int[][] dp = new int[n + 1][amount + 1];
// 初始话dp[0][0] = 1 dp[0][]=0
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= amount; j++) {
if (j < coins[i -1]) {
dp[i][j] = dp[i-1][j];
} else {
dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]]; // 可选或者不选择
}
}
}
return dp[n][amount];
}
我的另一种做题思路 这个还好理解
'''
凑出amount总金额最多需要amount个硬币(因为硬币最小面值1元)
dp[i][j]表示用i个硬币凑出总金额为j的种类有多少
dp[i][j] += dp[i-1][i-c](c -> coins)
则结果为:
res += dp[1...amount+1][amount]
即:1到amount+1个硬币凑出amount的总和
'''
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp = [[ 0 for _ in range(amount + 1)] for _ in range(amount + 1)]
for i in range(amount + 1):
dp[0][i] = 0
for j in range(amount + 1):
dp[j][0] = 0
for c in coins:
dp[1][c] = 1
for i in range(amount + 1):
for j in range(amount + 1):
for c in coins:
if j - c < 0:
continue
else:
dp[i][j] += dp[i-1][j-c]
res = 0
for i in range(amount + 1):
res += dp[i][amount]
return res
我的另一种做题思路 这个还好理解
''' 凑出amount总金额最多需要amount个硬币(因为硬币最小面值1元) dp[i][j]表示用i个硬币凑出总金额为j的种类有多少 dp[i][j] += dp[i-1][i-c](c -> coins) 则结果为: res += dp[1...amount+1][amount] 即:1到amount+1个硬币凑出amount的总和 '''
` class Solution:
def change(self, amount: int, coins: List[int]) -> int: dp = [[ 0 for _ in range(amount + 1)] for _ in range(amount + 1)] for i in range(amount + 1): dp[0][i] = 0 for j in range(amount + 1): dp[j][0] = 0 for c in coins: dp[1][c] = 1 for i in range(amount + 1): for j in range(amount + 1): for c in coins: if j - c < 0: continue else: dp[i][j] += dp[i-1][j-c] res = 0 for i in range(amount + 1): res += dp[i][amount] return res`
好像不行 有重复计算
稍微做个小优化,内层 for 循环的 j 可以直接从 coins[i - 1] 开始,这样就可以省去条件判断了,效率会高一些。