difficulty
 difficulty copied to clipboard
difficulty copied to clipboard
Best difficulty algorithm so far
I recommend one of the two following. They seem pretty much the same when the N of WWHM is 2x the N of EMA. In case I do not keep this page updated, I'll keep this blog post updated.
# Weighted-Weighted Harmonic Mean (WWHM) difficulty algorithm
# Original idea from Tom Harding (Deger8) called "WT-144"
# No limits, filtering, or tempering should be attempted.
# MTP should not be used.
# set constants
N=60
T=600 # coin's Target solvetime. Value can be anything.
adjust=0.99 # 0.98 for N=30, 0.99 for N=60
k = (N+1)/2 *adjust * T
# algorithm
previous_max=timestamp[height - N]
for ( i = height-N+1; i < height+1; i++) { # (N most recent blocks)
max_timestamp=max(timestamp[i], previous_max)
solvetime = max_timestamp - previous_max
solvetime=1 if solvetime < 1
solvetime = 10*T if solvetime > 10*T
previous_max=max_timestamp
j++
t += solvetime * j # give more weight to recent blocks
d +=D[i] # sum the difficulties
} # next i
t=T*N if t < T*N # in case of startup weirdness keep t sane
next_D = d * k / t
# limits do not need to be used because of the above solvetime restrictions
# but if you still want limits on D's change per block & expect max 5x hash rate
# changes or want to replace the solvetime restrictions, use
# limit = 5^(3/N)
# next_D = previous_D*limit if next_D > previous_D*limit
# next_D = previous_D/limit if next_D > previous_D/limit
=======================
# Jacob Eliosoff's EMA (exponential moving average)
# see https://en.wikipedia.org/wiki/Moving_average#Application_to_measuring_computer_performance
# ST = previous solvetime
# N=35 to 100 seems possible. Small N for small coins. N=70 for all might be best.
# MTP should not be used
ST = previous timestamp - timestamp before that
ST = max(T/100,min(T*10, ST))
next_D = previous_D * ( T/ST + e^(-ST/T/N) * (1-T/ST) )

This is the new best one. It is beneficial over simple N=70 only if sudden hash changes are >3x.
# Dynamic EMA difficulty algo (Jacob Eliosoff's EMA and Zawy's adjustable window).
# Bitcoin Cash dev (Amaury?) came up with the median of three to reduce timestamp errors.
# For EMA origins see
# https://en.wikipedia.org/wiki/Moving_average#Application_to_measuring_computer_performance
# "Dynamic" means it triggers to a faster-responding value for N if a substantial change in hashrate
# is detected. It increases from that event back to Nmax
Nmax=70 # max EMA window
Nmin=25 # min EMA window
A=10, B=2, C=0.37 # A,B,C = 10,2,0.37 or 20, 1.65 0.45,
# TS=timestamp, T=target solvetime, i.e. 600 seconds
# Find the most recent unusual 20-block event
for (i=height-Nmax to height) { # height=current block index
if ( (median(TS[i],TS[i-1],TS[i-2]) - median(TS[i-20],TS[i-21],TS[i-22]))/T/A > B
or
(median(TS[i],TS[i-1],TS[i-2]) - median(TS[i-20],TS[i-21],TS[i-22]))/T/A < C )
{ unusual_event=height - i + Nmin }
}
N = min(Nmax, unusual_event))
# now use the EMA difficulty algorithm with this N
Here are some comparisons under sudden hashrate changes and constant hashrate.

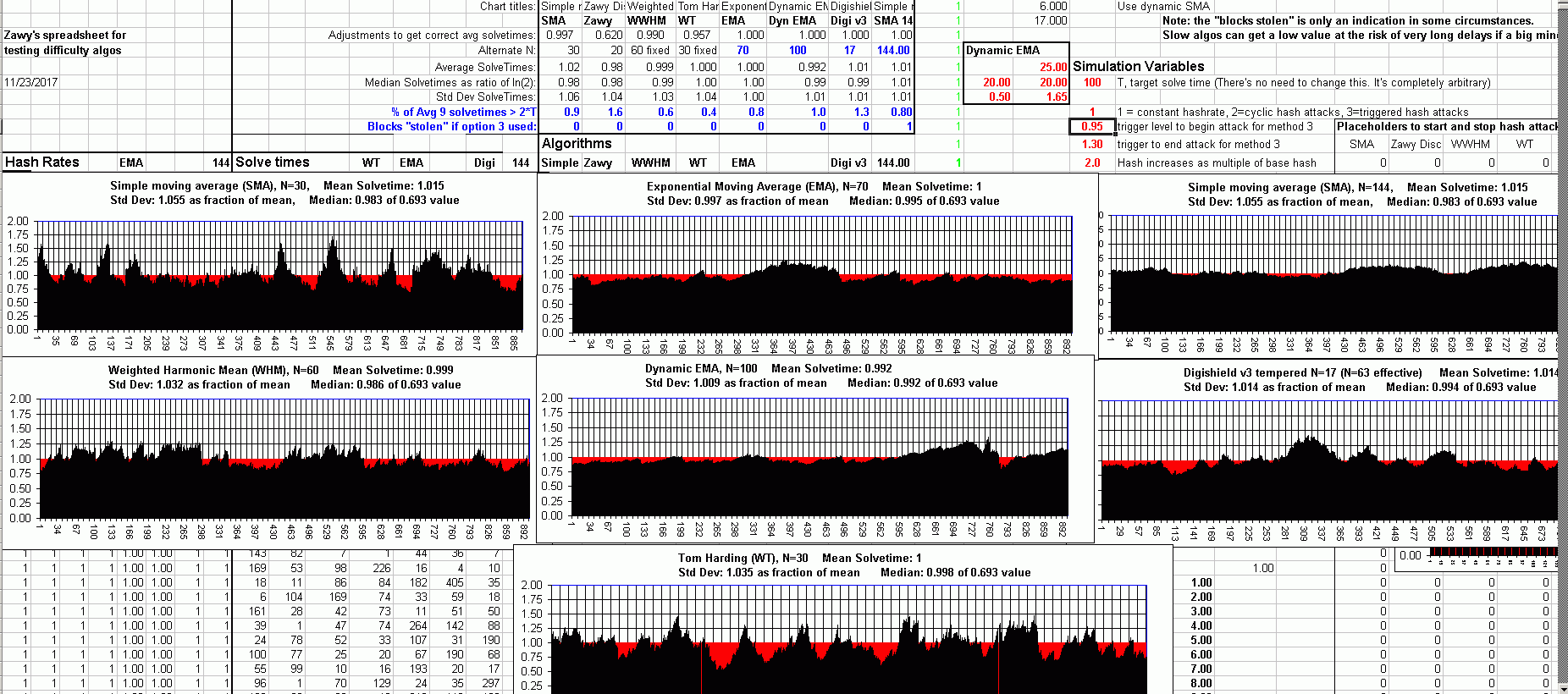
I corrected a code error in the previous post.
An updated version of this LWMA is now being used on 5 monero clones.