scikit-fem
scikit-fem copied to clipboard
kinnala
ElementLinePp(2) plotting incorrect
Comparing a one-dimensional simulation with higher order elements, I noticed a strange behavior of ElementLinePp() when used with p=2. Other values for p seem to be fine. Of course, in this special case it would anyways be better to use ElementLineP2(), as stated in the warning message.
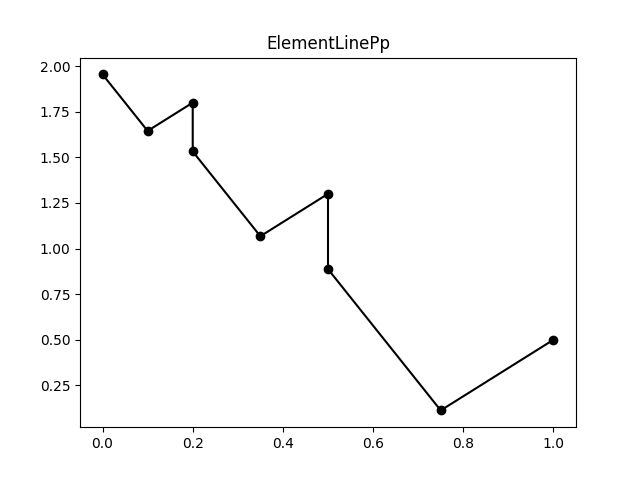
Example code:
import skfem
from skfem.models.poisson import laplace
from skfem.visuals.matplotlib import plot, show
mesh = skfem.MeshLine(p=[0, 0.2, 0.5, 1.0])
#element = skfem.ElementLineP2()
element = skfem.ElementLinePp(2)
basis = skfem.Basis(mesh, element)
A = skfem.asm(laplace, basis)
b = basis.zeros()
phi = basis.zeros()
phi[basis.get_dofs(lambda x: x == 0)] = -0.5
phi[basis.get_dofs(lambda x: x == 1.0)] = 2.0
phi = skfem.solve(*skfem.condense(A, b, x=phi, D=basis.get_dofs()))
ax = plot(basis, phi)
ax.set_title(f'{type(element).__name__}')
show()
Yes, it's again something to do with 1D plotting. Here is a workaround:
ax = plot(basis, phi, nrefs=0)
With nrefs=0 the plot does look correct, thanks for that hint!
Regardless of the plotting, the calculated values are still not identical:
With ElementLineP2():
phi = array([-5.00000000e-01, 8.32667268e-17, 7.50000000e-01, 2.00000000e+00,
-2.50000000e-01, 3.75000000e-01, 1.37500000e+00])
With ElementLinePp(2):
phi = array([-5.00000000e-01, 5.55111512e-17, 7.50000000e-01, 2.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00])
By the way, my code above was slightly wrong: I messed up the boundary identification. Replace
phi[basis.get_dofs(lambda x: x == 0)] = -0.5
phi[basis.get_dofs(lambda x: x == 1.0)] = 2.0
with
phi[basis.get_dofs(lambda x: x[0] == 0)] = -0.5
phi[basis.get_dofs(lambda x: x[0] == 1.0)] = 2.0
I believe that the difference is because ElementLineP2 uses nodal basis and ElementLinePp uses hierarchical basis.
I'm not entirely sure what that means. Is ElementLinePp(2) simply different from ElementLineP2() and cannot be used as a universal (but slower) substitute?
In a larger simulation, where I'm trying to calculate eigenmodes in 1d, I also get different results when using ElementLinePp(2) instead of ElementLineP2().
In most applications you can use either one of those but they don't give exactly the same result because the basis functions are different. There are infinite different bases you can use to represent quadratic polynomials. There are many different choices that are used in FEM depending on the use case.
We can leave this open because of the bug in skfem.visuals.matplotlib.plot for MeshLine1.
I cannot remember what was the remaining work and cannot deduce it by reading this, closing. The workaround is to specify nrefs=0, hierarchical bases cannot use nrefs>0.