WIP: Compute expected times per pathphone_idx.

[csukuangfj]

Closes #96

@danpovey Do you have any idea how to test the code? And I am not sure how the return value is used.

~I am using mbr_lats instead of den_lats as I find that phone_seqs from mbr_lats contains more zeros than that from den_lats.~

~I don't quite understand the normalization step from https://github.com/k2-fsa/snowfall/issues/96#issue-805274300 so it is not done in the code.~

Multiply the posteriors by the frame_idx and then sum over the columns of the sparse matrix of posteriors to get the total (frame_idx * occupation prob) for each seqphone_idx, and divide by the total occupation_prob for each seqphone_idx

[danpovey]

Great! Let me look at this to-morrow. The normalization step should not be needed if you used the 'phones' attribute with no repeats to create the sparse matrix. Instead of sum (weight * frame-index) it would be something like sum(weight * frame_index) / sum(weight) if there was normalization. Only necessary if the denominator is not bound to be 1.

[danpovey]

BTW for testing: just making sure that the computed average times are monotonic and not greater than the length of the utterances would be a good start.

[danpovey]

And for how the times are used:

• We'll probably use the durations as part of an embedding.
• The times themselves will be used to create embeddings from the output of the 1st-pass network, by interpolating between adjacent frames (whichever are closest to the average times).
• We'll need to compute times for the positions between the phones (and between the first and last phones, and the start/end of the file), too. The positions/blanks between phones will also have frames corresponding to them.

[csukuangfj]

I just checked the return value, shown below.

Assume there are two sequences and each has 1000 frames.

It is not strictly monotonic for the first 50 pathphone_idx. The last entry is 1000, which is equal to the number of input frames in the sequence.

[danpovey]

I think this might be due to normalization problems.. can you print the row-sums of the weights to check that they sum to 1.0?

[csukuangfj]

can you print the row-sums of the weights to check that they sum to 1.0?

An assertion is added to check this and it passes. https://github.com/k2-fsa/snowfall/blob/f6d3dcb4b0f1ab83024ba1fd9e8f92fe372db60d/snowfall/training/compute_expected_times.py#L135-L137

If I replace mbr_lats with den_lats, then the first 50 pathphone_idx's also seem to be monotonic. Please see the results below. (NOTE: It uses different random data from the previous screenshot.)

[csukuangfj]

Will replace the expected times for the even pathphone_idxs, which belong to the epsilon self-loops, with the average expected times of two neighboring phones.

[danpovey]

RE "If I replace mbr_lats with den_lats, then the first 50 pathphone_idx's also seem to be monotonic"... for me this is a bit strange. I think we should try to find what is the difference between the two graphs that causes this difference. There should be no constraint that an epsilon between phones should always be taken, so IMO it should be possible that for the epsilon positions, we would sometimes get total-counts that are less than one. Maybe not for every minibatch, but in general. It's very strange if not.

[csukuangfj]

we would sometimes get total-counts that are less than one

Is total-counts the same as total-occupation?

[csukuangfj]

The total_occupation[:50]'s for den_lats and mbr_lats are given below:

[csukuangfj]

Differences between den_lats and mbr_lats

phones

• The phones attribute of den_graph is from k2.compose(ctc_topo, P_with_self_loops)
• The phones attribute of decoding_graph is from k2.compose(ctc_topo, LG)

intersect

• den_lats is generated from k2.intersect_dense(den_graph, dense_fsa_vec, 10.0)
• mbr_lats is generated from

mbr_lats = k2.intersect_dense_pruned(decoding_graph,
                                     dense_fsa_vec,
                                     20.0,
                                     7.0,
                                     30,
                                     10000,
                                     seqframe_idx_name='seqframe_idx')

[danpovey]

I don't see, in the current code at least in my branch I'm working on, anywhere where the 'phones' attribute is set in den_graph.

[csukuangfj]

Here is the output for the test script. You can see that mbr_lats.phones and den_lats.phones are both torch.Tensor's

abc.txt

[danpovey]

I think I understand the reason for the difference now. It has to do with the language model. LG.fst will penalize insertion of phones because it has nonzero LM probabilities, but the P matrix has zero scores. So the decoding graph will P (den_graph) will tend to decode substantially more phones than the one with LG (mbr_graph).

[csukuangfj]

OK. BTW did you already look at the decoding graph that you used to generate den_lats

Here is a text form of den. Looks like it is an acceptor. I don't see any problems with it.

den.txt

[csukuangfj]

So the decoding graph will P (den_graph) will tend to decode substantially more phones than the one with LG (mbr_graph).

Will initialize P.scores randomly to see whether it makes a difference.

[danpovey]

I think the key thing is that the scores should be mostly negative. make_stochastic should do this.

On Tue, Feb 23, 2021 at 9:27 PM Fangjun Kuang [email protected] wrote:

So the decoding graph will P (den_graph) will tend to decode substantially more phones than the one with LG (mbr_graph).

Will initialize P.scores randomly to see whether it makes a difference.

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHub https://github.com/k2-fsa/snowfall/pull/106#issuecomment-784202094, or unsubscribe https://github.com/notifications/unsubscribe-auth/AAZFLOYOXLIIRIKD5CZQZ53TAOUMRANCNFSM4YAAWE7Q .

[csukuangfj]

After making P.scores stochastic, the output of the test script is a2.txt

Now there are indeed more 0s in the phone_seqs from den_lats than before.

---

Since the expected times for self-loops pathphone_idx are interpolated (excluding the first entry, which has no left neighbor), you can see that it is monotonic.

But it does not satisfy the following comment:

so IMO it should be possible that for the epsilon positions, we would sometimes get total-counts that are less than one. Maybe not for every minibatch, but in general. It's very strange if not.

The total-occupation for both lattices has values greater than 1, especially for mbr_lats.

den_lats

before removing 0 tensor([   0, 1001, 2002, 3003, 4004], dtype=torch.int32)
after removing 0 tensor([   0,  420,  853, 1262, 1681], dtype=torch.int32)

total_occupation[:50]
 tensor([0.4892, 1.0000, 1.0897, 1.0000, 1.0026, 1.0000, 0.9779, 1.0000, 1.1075,
        1.0000, 0.9518, 1.0000, 1.2959, 1.0000, 1.2585, 1.0000, 1.2386, 1.0000,
        1.2876, 1.0000, 1.1388, 1.0000, 1.4333, 1.0000, 1.2247, 1.0000, 1.2209,
        1.0000, 1.2490, 1.0000, 1.2151, 1.0000, 1.3507, 1.0000, 1.2178, 1.0000,
        1.3574, 1.0000, 1.3590, 1.0000, 1.4166, 1.0000, 1.4708, 1.0000, 1.3837,
        1.0000, 1.3361, 1.0000, 1.2814, 1.0000], dtype=torch.float64)
expected_times[:50]
tensor([ 0.6353,  0.4892,  1.5341,  2.5789,  3.5802,  4.5815,  5.5704,  6.5594,
         7.6131,  8.6669,  9.6428, 10.6187, 11.7667, 12.9146, 14.0438, 15.1731,
        16.2923, 17.4116, 18.5554, 19.6993, 20.7687, 21.8381, 23.0547, 24.2713,
        25.3837, 26.4960, 27.6064, 28.7169, 29.8414, 30.9659, 32.0734, 33.1810,
        34.3563, 35.5316, 36.6405, 37.7494, 38.9281, 40.1068, 41.2864, 42.4659,
        43.6741, 44.8824, 46.1178, 47.3533, 48.5451, 49.7370, 50.9051, 52.0731,
        53.2139, 54.3546], dtype=torch.float64)

mbr_lats

before removing 0 tensor([   0, 1001, 2002, 3003, 4004], dtype=torch.int32)
after removing 0 tensor([  0, 211, 421, 593, 766], dtype=torch.int32)
total_occupation[:50]
 tensor([1.4870, 1.0000, 2.3758, 1.0000, 2.2955, 1.0000, 3.1216, 1.0000, 3.5592,
        1.0000, 2.7304, 1.0000, 3.4665, 1.0000, 2.7669, 1.0000, 2.9250, 1.0000,
        3.2082, 1.0000, 3.7151, 1.0000, 2.9975, 1.0000, 4.1651, 1.0000, 3.4588,
        1.0000, 3.4414, 1.0000, 4.3693, 1.0000, 3.5034, 1.0000, 3.8095, 1.0000,
        3.4294, 1.0000, 3.8266, 1.0000, 4.0932, 1.0000, 3.3093, 1.0000, 3.1595,
        1.0000, 4.0714, 1.0000, 3.4673, 1.0000], dtype=torch.float64)
expected_times[:50]
tensor([  1.2857,   1.4870,   3.1749,   4.8628,   6.5106,   8.1583,  10.2191,
         12.2799,  14.5595,  16.8391,  18.7043,  20.5695,  22.8028,  25.0360,
         26.9194,  28.8029,  30.7654,  32.7278,  34.8320,  36.9361,  39.2936,
         41.6512,  43.6499,  45.6486,  48.2312,  50.8137,  53.0431,  55.2725,
         57.4932,  59.7139,  62.3985,  65.0831,  67.3348,  69.5865,  71.9913,
         74.3960,  76.6107,  78.8254,  81.2387,  83.6520,  86.1986,  88.7452,
         90.8998,  93.0544,  95.1342,  97.2139,  99.7497, 102.2854, 104.5190,
        106.7527], dtype=torch.float64)

[danpovey]

There are some values less than one, e.g. 0.4892 or 0.9779 from den_lats. I think thiss is OK. Maybe there's something about the data or how the model was trained (if you're using a trained model) that makes this so.

[csukuangfj]

The training is able to run now. Both the first pass tot_scores and the second pass tot_scores are decreasing over time.

TODOs

• [x] Visualize the tot_scores from different passes in tensorboard
• [x] Save/Load second pass model to/from checkpoint
• [ ] ~Increase num_paths once memory optimization for intersect_dense is done~
• [ ] Post decoding results of the trained model

[danpovey]

Amazing!! Well done!

[csukuangfj]

Attached are the training and decoding (for the 0th epoch) logs of this pull-request (using the last commit).

log-train-2021-03-05-17-29-07.txt log-decode-2021-03-05-21-24-52.txt

Part of the training log is posted below:

2021-03-05 17:29:20,785 INFO [mmi_bigram_embeddings_train.py:644] epoch 0, learning rate 0.001
2021-03-05 17:29:22,720 INFO [mmi_bigram_embeddings_train.py:368] batch 0, epoch 0/10 global average objf: 3.071507 over 3297.0 global average second_pass objf: 1.224912 over 3297.0 frames (100.0% kept), current batch average objf: 3.071507 over 3297 frames (100.0% kept) current batch average second_pass objf: 1.224912) avg time waiting for batch 0.737s
2021-03-05 17:29:23,360 INFO [mmi_bigram_embeddings_train.py:368] batch 1, epoch 0/10 global average objf: 3.245797 over 6601.0 global average second_pass objf: 1.290150 over 6601.0 frames (100.0% kept), current batch average objf: 3.419715 over 3304 frames (100.0% kept) current batch average second_pass objf: 1.355249) avg time waiting for batch 0.737s
2021-03-05 17:29:23,967 INFO [mmi_bigram_embeddings_train.py:368] batch 2, epoch 0/10 global average objf: 3.188134 over 9617.0 global average second_pass objf: 0.903973 over 9617.0 frames (100.0% kept), current batch average objf: 3.061929 over 3016 frames (100.0% kept) current batch average second_pass objf: 0.058763) avg time waiting for batch 0.369s
2021-03-05 17:29:24,443 INFO [mmi_bigram_embeddings_train.py:368] batch 3, epoch 0/10 global average objf: 3.003953 over 12854.0 global average second_pass objf: 0.730059 over 12854.0 frames (100.0% kept), current batch average objf: 2.456756 over 3237 frames (100.0% kept) current batch average second_pass objf: 0.213366) avg time waiting for batch 0.246s
2021-03-05 17:29:25,037 INFO [mmi_bigram_embeddings_train.py:368] batch 4, epoch 0/10 global average objf: 2.921010 over 15876.0 global average second_pass objf: 0.676803 over 15876.0 frames (100.0% kept), current batch average objf: 2.568215 over 3022 frames (100.0% kept) current batch average second_pass objf: 0.450280) avg time waiting for batch 0.186s

....


2021-03-05 21:30:34,837 INFO [mmi_bigram_embeddings_train.py:368] batch 4051, epoch 1/10 global average objf: 0.563265 over 12648255.0 global average second_pass objf: 0.290650 over 12648255.0 frames (100.0% kept), current batch average objf: 0.509593 over 2888 frames (100.0% kept) current batch average second_pass objf: 0.262456) avg time waiting for batch 0.003s
2021-03-05 21:30:35,731 INFO [mmi_bigram_embeddings_train.py:368] batch 4052, epoch 1/10 global average objf: 0.563226 over 12651537.0 global average second_pass objf: 0.290629 over 12651537.0 frames (100.0% kept), current batch average objf: 0.413871 over 3282 frames (100.0% kept) current batch average second_pass objf: 0.207072) avg time waiting for batch 0.003s
2021-03-05 21:30:36,639 INFO [mmi_bigram_embeddings_train.py:368] batch 4053, epoch 1/10 global average objf: 0.563249 over 12654410.0 global average second_pass objf: 0.290639 over 12654410.0 frames (100.0% kept), current batch average objf: 0.663711 over 2873 frames (100.0% kept) current batch average second_pass objf: 0.337996) avg time waiting for batch 0.003s
2021-03-05 21:30:37,557 INFO [mmi_bigram_embeddings_train.py:368] batch 4054, epoch 1/10 global average objf: 0.563294 over 12657682.0 global average second_pass objf: 0.290663 over 12657682.0 frames (100.0% kept), current batch average objf: 0.737876 over 3272 frames (100.0% kept) current batch average second_pass objf: 0.382271) avg time waiting for batch 0.003s
2021-03-05 21:30:38,551 INFO [mmi_bigram_embeddings_train.py:368] batch 4055, epoch 1/10 global average objf: 0.563311 over 12661003.0 global average second_pass objf: 0.290673 over 12661003.0 frames (100.0% kept), current batch average objf: 0.629145 over 3321 frames (100.0% kept) current batch average second_pass objf: 0.329582) avg time waiting for batch 0.003s

The decoding result of epoch-0.pt is

2021-03-05 21:26:37,701 INFO [mmi_bigram_embeddings_decode.py:258] %WER 16.61% [8734 / 52576, 767 ins, 1480 del, 6487 sub ]

Will add more decoding results from different epochs once the training is done.

[danpovey]

Wow, very fast progress! Decoding result looks similar to existing epoch-0 decoding. We'll see..

On Fri, Mar 5, 2021 at 9:38 PM Fangjun Kuang [email protected] wrote:

Attached are the training and decoding (for the 0th epoch) logs of this pull-request (using the last commit).

log-train-2021-03-05-17-29-07.txt https://github.com/k2-fsa/snowfall/files/6090748/log-train-2021-03-05-17-29-07.txt log-decode-2021-03-05-21-24-52.txt https://github.com/k2-fsa/snowfall/files/6090749/log-decode-2021-03-05-21-24-52.txt

Part of the training log is posted below:

2021-03-05 17:29:20,785 INFO [mmi_bigram_embeddings_train.py:644] epoch 0, learning rate 0.001 2021-03-05 17:29:22,720 INFO [mmi_bigram_embeddings_train.py:368] batch 0, epoch 0/10 global average objf: 3.071507 over 3297.0 global average second_pass objf: 1.224912 over 3297.0 frames (100.0% kept), current batch average objf: 3.071507 over 3297 frames (100.0% kept) current batch average second_pass objf: 1.224912) avg time waiting for batch 0.737s 2021-03-05 17:29:23,360 INFO [mmi_bigram_embeddings_train.py:368] batch 1, epoch 0/10 global average objf: 3.245797 over 6601.0 global average second_pass objf: 1.290150 over 6601.0 frames (100.0% kept), current batch average objf: 3.419715 over 3304 frames (100.0% kept) current batch average second_pass objf: 1.355249) avg time waiting for batch 0.737s 2021-03-05 17:29:23,967 INFO [mmi_bigram_embeddings_train.py:368] batch 2, epoch 0/10 global average objf: 3.188134 over 9617.0 global average second_pass objf: 0.903973 over 9617.0 frames (100.0% kept), current batch average objf: 3.061929 over 3016 frames (100.0% kept) current batch average second_pass objf: 0.058763) avg time waiting for batch 0.369s 2021-03-05 17:29:24,443 INFO [mmi_bigram_embeddings_train.py:368] batch 3, epoch 0/10 global average objf: 3.003953 over 12854.0 global average second_pass objf: 0.730059 over 12854.0 frames (100.0% kept), current batch average objf: 2.456756 over 3237 frames (100.0% kept) current batch average second_pass objf: 0.213366) avg time waiting for batch 0.246s 2021-03-05 17:29:25,037 INFO [mmi_bigram_embeddings_train.py:368] batch 4, epoch 0/10 global average objf: 2.921010 over 15876.0 global average second_pass objf: 0.676803 over 15876.0 frames (100.0% kept), current batch average objf: 2.568215 over 3022 frames (100.0% kept) current batch average second_pass objf: 0.450280) avg time waiting for batch 0.186s

....

2021-03-05 21:30:34,837 INFO [mmi_bigram_embeddings_train.py:368] batch 4051, epoch 1/10 global average objf: 0.563265 over 12648255.0 global average second_pass objf: 0.290650 over 12648255.0 frames (100.0% kept), current batch average objf: 0.509593 over 2888 frames (100.0% kept) current batch average second_pass objf: 0.262456) avg time waiting for batch 0.003s 2021-03-05 21:30:35,731 INFO [mmi_bigram_embeddings_train.py:368] batch 4052, epoch 1/10 global average objf: 0.563226 over 12651537.0 global average second_pass objf: 0.290629 over 12651537.0 frames (100.0% kept), current batch average objf: 0.413871 over 3282 frames (100.0% kept) current batch average second_pass objf: 0.207072) avg time waiting for batch 0.003s 2021-03-05 21:30:36,639 INFO [mmi_bigram_embeddings_train.py:368] batch 4053, epoch 1/10 global average objf: 0.563249 over 12654410.0 global average second_pass objf: 0.290639 over 12654410.0 frames (100.0% kept), current batch average objf: 0.663711 over 2873 frames (100.0% kept) current batch average second_pass objf: 0.337996) avg time waiting for batch 0.003s 2021-03-05 21:30:37,557 INFO [mmi_bigram_embeddings_train.py:368] batch 4054, epoch 1/10 global average objf: 0.563294 over 12657682.0 global average second_pass objf: 0.290663 over 12657682.0 frames (100.0% kept), current batch average objf: 0.737876 over 3272 frames (100.0% kept) current batch average second_pass objf: 0.382271) avg time waiting for batch 0.003s 2021-03-05 21:30:38,551 INFO [mmi_bigram_embeddings_train.py:368] batch 4055, epoch 1/10 global average objf: 0.563311 over 12661003.0 global average second_pass objf: 0.290673 over 12661003.0 frames (100.0% kept), current batch average objf: 0.629145 over 3321 frames (100.0% kept) current batch average second_pass objf: 0.329582) avg time waiting for batch 0.003s

The decoding result of epoch-0.pt is

2021-03-05 21:26:37,701 INFO [mmi_bigram_embeddings_decode.py:258] %WER 16.61% [8734 / 52576, 767 ins, 1480 del, 6487 sub ]

Will add more decoding results from different epochs once the training is done.

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHub https://github.com/k2-fsa/snowfall/pull/106#issuecomment-791424379, or unsubscribe https://github.com/notifications/unsubscribe-auth/AAZFLOZMEMNX354PNHAXQ33TCDNGFANCNFSM4YAAWE7Q .

[danpovey]

BTW, regarding decoding from the 2nd pass (my understanding is that you are not yet doing this...) something that would be easier to implement would be to do it with 1-best: i.e. compute the 1-best path from the 1st decode, and then in the second decode (with full decoding graph) also just take the 1-best path. That would be easier to implement and of course faster than some kind of voting scheme. Eventually we'll probably want to do this with some ROVER-type method, which would generalize better to long utterances where in general we won't get repeats of the same utterance among the n-best paths.

On Fri, Mar 5, 2021 at 10:10 PM Daniel Povey [email protected] wrote:

Wow, very fast progress! Decoding result looks similar to existing epoch-0 decoding. We'll see..

On Fri, Mar 5, 2021 at 9:38 PM Fangjun Kuang [email protected] wrote:

Attached are the training and decoding (for the 0th epoch) logs of this pull-request (using the last commit).

log-train-2021-03-05-17-29-07.txt https://github.com/k2-fsa/snowfall/files/6090748/log-train-2021-03-05-17-29-07.txt log-decode-2021-03-05-21-24-52.txt https://github.com/k2-fsa/snowfall/files/6090749/log-decode-2021-03-05-21-24-52.txt

Part of the training log is posted below:

2021-03-05 17:29:20,785 INFO [mmi_bigram_embeddings_train.py:644] epoch 0, learning rate 0.001 2021-03-05 17:29:22,720 INFO [mmi_bigram_embeddings_train.py:368] batch 0, epoch 0/10 global average objf: 3.071507 over 3297.0 global average second_pass objf: 1.224912 over 3297.0 frames (100.0% kept), current batch average objf: 3.071507 over 3297 frames (100.0% kept) current batch average second_pass objf: 1.224912) avg time waiting for batch 0.737s 2021-03-05 17:29:23,360 INFO [mmi_bigram_embeddings_train.py:368] batch 1, epoch 0/10 global average objf: 3.245797 over 6601.0 global average second_pass objf: 1.290150 over 6601.0 frames (100.0% kept), current batch average objf: 3.419715 over 3304 frames (100.0% kept) current batch average second_pass objf: 1.355249) avg time waiting for batch 0.737s 2021-03-05 17:29:23,967 INFO [mmi_bigram_embeddings_train.py:368] batch 2, epoch 0/10 global average objf: 3.188134 over 9617.0 global average second_pass objf: 0.903973 over 9617.0 frames (100.0% kept), current batch average objf: 3.061929 over 3016 frames (100.0% kept) current batch average second_pass objf: 0.058763) avg time waiting for batch 0.369s 2021-03-05 17:29:24,443 INFO [mmi_bigram_embeddings_train.py:368] batch 3, epoch 0/10 global average objf: 3.003953 over 12854.0 global average second_pass objf: 0.730059 over 12854.0 frames (100.0% kept), current batch average objf: 2.456756 over 3237 frames (100.0% kept) current batch average second_pass objf: 0.213366) avg time waiting for batch 0.246s 2021-03-05 17:29:25,037 INFO [mmi_bigram_embeddings_train.py:368] batch 4, epoch 0/10 global average objf: 2.921010 over 15876.0 global average second_pass objf: 0.676803 over 15876.0 frames (100.0% kept), current batch average objf: 2.568215 over 3022 frames (100.0% kept) current batch average second_pass objf: 0.450280) avg time waiting for batch 0.186s

....

2021-03-05 21:30:34,837 INFO [mmi_bigram_embeddings_train.py:368] batch 4051, epoch 1/10 global average objf: 0.563265 over 12648255.0 global average second_pass objf: 0.290650 over 12648255.0 frames (100.0% kept), current batch average objf: 0.509593 over 2888 frames (100.0% kept) current batch average second_pass objf: 0.262456) avg time waiting for batch 0.003s 2021-03-05 21:30:35,731 INFO [mmi_bigram_embeddings_train.py:368] batch 4052, epoch 1/10 global average objf: 0.563226 over 12651537.0 global average second_pass objf: 0.290629 over 12651537.0 frames (100.0% kept), current batch average objf: 0.413871 over 3282 frames (100.0% kept) current batch average second_pass objf: 0.207072) avg time waiting for batch 0.003s 2021-03-05 21:30:36,639 INFO [mmi_bigram_embeddings_train.py:368] batch 4053, epoch 1/10 global average objf: 0.563249 over 12654410.0 global average second_pass objf: 0.290639 over 12654410.0 frames (100.0% kept), current batch average objf: 0.663711 over 2873 frames (100.0% kept) current batch average second_pass objf: 0.337996) avg time waiting for batch 0.003s 2021-03-05 21:30:37,557 INFO [mmi_bigram_embeddings_train.py:368] batch 4054, epoch 1/10 global average objf: 0.563294 over 12657682.0 global average second_pass objf: 0.290663 over 12657682.0 frames (100.0% kept), current batch average objf: 0.737876 over 3272 frames (100.0% kept) current batch average second_pass objf: 0.382271) avg time waiting for batch 0.003s 2021-03-05 21:30:38,551 INFO [mmi_bigram_embeddings_train.py:368] batch 4055, epoch 1/10 global average objf: 0.563311 over 12661003.0 global average second_pass objf: 0.290673 over 12661003.0 frames (100.0% kept), current batch average objf: 0.629145 over 3321 frames (100.0% kept) current batch average second_pass objf: 0.329582) avg time waiting for batch 0.003s

The decoding result of epoch-0.pt is

2021-03-05 21:26:37,701 INFO [mmi_bigram_embeddings_decode.py:258] %WER 16.61% [8734 / 52576, 767 ins, 1480 del, 6487 sub ]

Will add more decoding results from different epochs once the training is done.

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHub https://github.com/k2-fsa/snowfall/pull/106#issuecomment-791424379, or unsubscribe https://github.com/notifications/unsubscribe-auth/AAZFLOZMEMNX354PNHAXQ33TCDNGFANCNFSM4YAAWE7Q .

[csukuangfj]

It raises an exception in the 8th epoch.

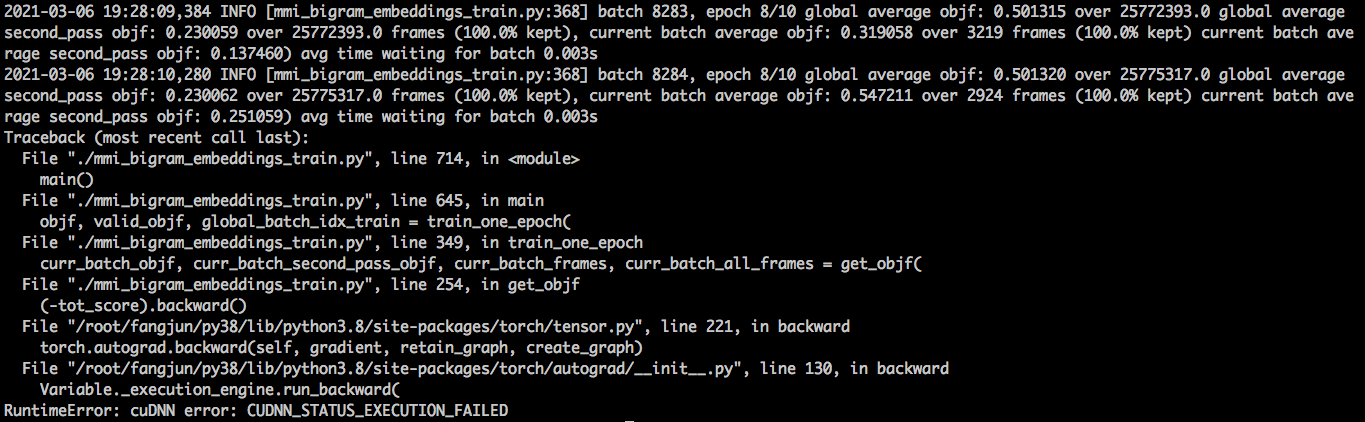
The WERs from epoch 0 to epoch 7 are not very good, shown below. It uses the same decoding script as mmi_bigram_decode.py

# epoch 0
2021-03-05 21:26:37,701 INFO [mmi_bigram_embeddings_decode.py:258] %WER 16.61% [8734 / 52576, 767 ins, 1480 del, 6487 sub ]

# epoch 1
2021-03-06 07:23:10,169 INFO [mmi_bigram_embeddings_decode.py:258] %WER 14.82% [7790 / 52576, 771 ins, 1085 del, 5934 sub ]

# epoch 2
2021-03-06 07:24:21,153 INFO [mmi_bigram_embeddings_decode.py:258] %WER 14.08% [7402 / 52576, 709 ins, 1052 del, 5641 sub ]

# epoch 3
2021-03-06 07:25:54,501 INFO [mmi_bigram_embeddings_decode.py:258] %WER 15.59% [8196 / 52576, 741 ins, 1337 del, 6118 sub ]

# epoch 4
2021-03-06 10:16:22,803 INFO [mmi_bigram_embeddings_decode.py:258] %WER 15.10% [7937 / 52576, 748 ins, 1124 del, 6065 sub ]

# epoch 5
2021-03-06 14:13:09,415 INFO [mmi_bigram_embeddings_decode.py:258] %WER 15.86% [8337 / 52576, 790 ins, 1233 del, 6314 sub ]

# epoch 6
2021-03-07 09:16:15,860 INFO [mmi_bigram_embeddings_decode.py:258] %WER 17.78% [9348 / 52576, 782 ins, 1586 del, 6980 sub ]

# epoch 7
2021-03-07 09:17:56,069 INFO [mmi_bigram_embeddings_decode.py:258] %WER 16.60% [8729 / 52576, 740 ins, 1425 del, 6564 sub ]

[csukuangfj]

BTW, regarding decoding from the 2nd pass (my understanding is that you are not yet doing this...) something that would be easier to implement would be to do it with 1-best:

The second pass model is currently not used in the decoding script. Will try to implement it as you proposed.

[danpovey]

perhaps wers are degraded because the derivatives from second pass affect nnet output values... could perhaps modify initial nnet to produce two outputs, one without log softmax? i wonder whether the failure was repeatable...

On Sunday, March 7, 2021, Fangjun Kuang [email protected] wrote:

BTW, regarding decoding from the 2nd pass (my understanding is that you are not yet doing this...) something that would be easier to implement would be to do it with 1-best:

The second pass model is currently not used in the decoding script. Will try to implement it as you proposed.

— You are receiving this because you were mentioned. Reply to this email directly, view it on GitHub https://github.com/k2-fsa/snowfall/pull/106#issuecomment-792149829, or unsubscribe https://github.com/notifications/unsubscribe-auth/AAZFLO43PLBEQISNA5CNFSLTCLKOPANCNFSM4YAAWE7Q .

[danpovey]

Something else:  I think we should try to figure out a good interface for an "encoder", and not have this be one huge mass of code. I'm trying to write down here the various objects we're dealing with, and name things, so that people may get ideas about how to structure the code.

(i) n-best lists containing phones, as a 3-d Tensor with indexes [seq][nbest][phone] ... at some point we'll interpolate epsilons between each phone to get a 3-d Tensor also indexed [seq][nbest][phone] but with epsilons in between; the (seq+nbest)_idx will be called a path_idx (an idx01) and the (seq+nbest+phone)_idx would be a pathphone_idx.
We can distinguish between raw_nbest (no epsilons) and padded_nbest (with epsilons).

  NOTE: In the future we may decide to have versions of these n-best lists where there
  are more than 1 epsilon between phones, although in that case we won't be able to identify
  the epsilon with the self-loop of the phone; we would have to introduce the epsilons at a later
  stage in that case.

(ii) create graphs from these n-best lists, align, get posteriors. We'll have a sparse matrix of posteriors with indexes [pathphone_idx][seqframe_idx]. (iii) get expected times (in frames) for each phone. Suppose this is a Tensor of float or double indexed by [pathphone_idx], containing frame_idx as float. (iv) We can can turn the expected times (above) into a sparse matrix of alignments with indexes [pathphone_idx][seqframe_idx]. (The epsilon positions may have to be interpolated as, in general, they won't always exist.) NOTE: this "alignment matrix" is like the "sparse matrix of posteriors" mentioned above (assuming we normalize the matrix of posteriors per row to get an "alignment matrix"); "alignment matrix" implies the rows sum to one. We could get two copies of the embeddings, one from each; although we'd need some kind of backoff mechanism to deal with rows of the "sparse matrix of posteriors" that had zero count, which is possible in principle for epsilon position. (v) Various kinds of embeddings. Let's say an embedding indexed by pathphone_idx is a Tensor with indexes [pathphone_idx][feature]. Examples of embeddings: - duration - absolute time - nnet output from 1st pass - hidden layer output - mfccs etc. (would need to deal correctly with subsampling). - also a bunch of embeddings can be appended together and will still be an embedding (vi) We need a process to take irregular-sized/ragged embeddings and fit them into a rectangular tensor, and keep track of the segment information. This process is quite similar to the process of creating the minibatch in the 1st place (starting from MFCCs). (We might be able to figure out a suitable interface for this...)

(vii) After decoding the 2nd pass (this will happen in test time) we'll get an nbest list indexed [path_idx][nbest][phone]. Conceptually this is indexed [seq][nbest][nbest][phone]. One way to decode is to uniq the sequences and count.

[csukuangfj]

After regenerating the features with the latest lhtose and reducing num_paths from 8 to 5, the WERs become better. The tensorboard log is at https://tensorboard.dev/experiment/EEMXUKABQ6WyoxxPmly3qw/#scalars

# epoch 0
2021-03-08 15:16:55,007 INFO [mmi_bigram_embeddings_decode.py:258] %WER 16.57% [8712 / 52576, 771 ins, 1343 del, 6598 sub ]

# epoch 1
2021-03-08 17:29:14,856 INFO [mmi_bigram_embeddings_decode.py:271] %WER 13.21% [6946 / 52576, 793 ins, 776 del, 5377 sub ]

# epoch 2
2021-03-08 19:00:00,512 INFO [mmi_bigram_embeddings_decode.py:271] %WER 12.03% [6326 / 52576, 720 ins, 681 del, 4925 sub ]

# epoch 3
2021-03-08 21:31:04,285 INFO [mmi_bigram_embeddings_decode.py:258] %WER 12.18% [6404 / 52576, 785 ins, 668 del, 4951 sub ]

However, it degrades from epoch 2 to epoch 3.

Will try two things tomorrow:

(1) Add another linear layer to the first pass model, which is placed before the log softmax layer. Its output is used to compute embeddings.

(2) Decoding from the second pass by following

something that would be easier to implement would be to do it with 1-best: i.e. compute the 1-best path from the 1st decode, and then in the second decode (with full decoding graph) also just take the 1-best path. That would be easier to implement and of course faster than some kind of voting scheme.

[danpovey]

Thanks! I really don't understand why reducing num_paths from 8 to 5 should help. It feels like some kind of bug but I can't see one. But it's possible that the auxiliary objective somehow degrades the output by biasing the log-likes somehow. I thought there might be some bug that made the secondary objective have too-large scale, but I can't see such a bug.