Set length property on typed functions

[ChristopherChudzicki]

Note: This is related to #154, but I think smaller in scope and could be handled separately if this is decided to be a good idea.

I've noticed that all typed functions have length 2. For example:

const f = math.evaluate('f(w,x,y,z) = w*x*y*z')
console.log(f.length) // 2

whereas I would expect f.length to be 4.

Suggestion:

• if a typed function has only one signature, its length should be the length of that signature.
• alternatively the length of a typed function should be the length of its first signature.

Notes:

• #154 seems very useful, but I think that having a reasonable length property would also be useful. It would make typed functions behave more like "normal" js functions. Additionally, there's less (imo) of a design issue here since the API would be much simpler.

• My particular motivation is to supply a random sample to the result of math.evaluate so I can tell if evaluating the function would result in an error. For example, const f = math.evaluate(f(x) = 2^[1,2,3]) evaluates fine. but calling f(anything) will throw an error. For this purple, having a valid sample in f's domain isn't really necessary (evaluating to NaN would be fine) but I do need to know how many params it has.

  My current workaround is getting the number of params from the FunctionAssignmentNode, but I'd prefer to implement the "sample evaluation of f" logic in a way that is agnostic as to whether f is coming from MathJs or from some other source.

[josdejong]

Thanks for your suggestions.

The reason that f.length is always 2 is due to how typed-function currently optimizes functions: it has a "fast" outer function with two arguments defined, which can quickly check the signatures of up to 6 signatures with up to two arguments. If no match is found, it falls back to the "generic" implementation which tests all signatures:

https://github.com/josdejong/typed-function/blob/477c1e829230ea5badc119ac391ee731f856d42d/src/typed-function.mjs#L1501-L1514

The reason for this outer function was optimization. It may well be that it doesn't do much nowadays, and we can add more "fast" optimized outer functions, like we could hard code optimizations for functions having a single signatures and either 1, 2, 3, or 4 arguments. This would come at the cost of more code. It is hard to benchmark these things in a reliable way, and it may be hard to figure out what "common" cases are worth having their own optimized function.

Can you explain your original use case further? I can't reproduce and/or understand what you mean exactly because the part of your example 2^[1,2,3] cannot be executed (having a matrix on the right side of pow), that just throws an error when evaluating but this seems unrelated to the topic.

[ChristopherChudzicki]

Regarding the initial motivation... consider https://www.math3d.org/th3qdbt2L

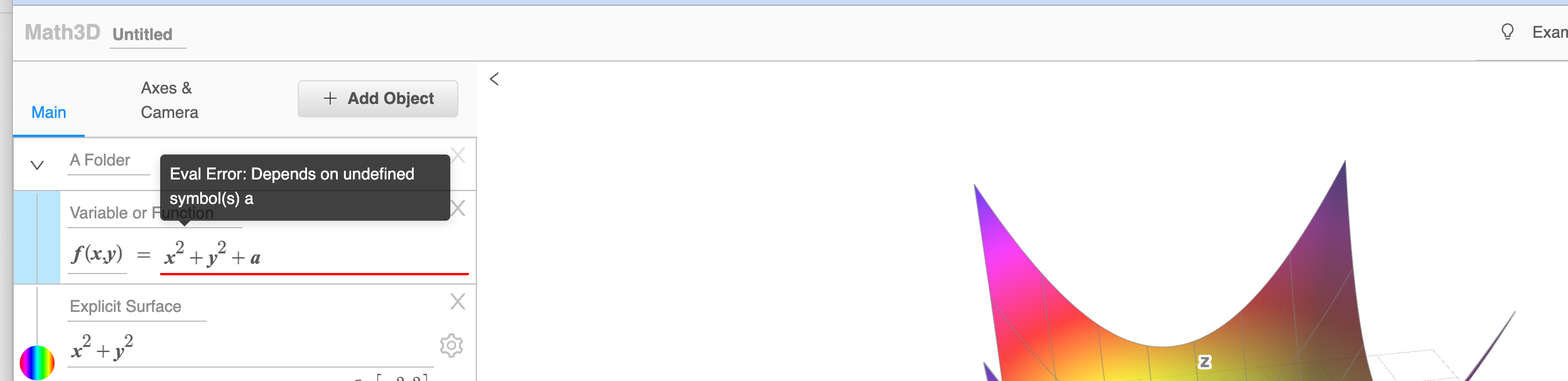
Evaluations like

// this script runs without errors
const math = require('mathjs')
const f1 = math.evaluate("f(x, y) = x^2 + y^2 + a") // "a" undefined
const f2 = math.evaluate("f(x) = 2^[x,x,x]")

all evaluate without errors in MathJS. It's only when f1 or f2 are themselves called that errors occur. Note: I think this behavior is entirely reasonable; certainly for f1, perhaps a little less for f2, but still not unreasonable from a software perspective.

But when building an app like the one pictured above, I'd like to tell users about those when the define the functions, rather than when they evaluate the functions.

So to do that, I've been evaluating the functions at a random point in their domains: f1(rand1, rand2), etc. But that means I need to be able to pick a point in their domain. Well ok, I don't really have any idea if it's in the actual domain, but if the function evaluates to NaN, that's valid as far as I'm concerned.

So how to pick a point in the domain? Some options:

1. Inspect the original expression and look at the FunctionAssignmentNode's params property. This usually works. But it could never work for something like f = sin or f = atan2 since those get parsed as AssignmentNode even though they evaluate to functions.
2. Look at the JS function's length property. In the JS world I would expect this to work for anything without rest parameters (or using the old arguments object). Since f1, f2, sin, and atan2 accept a fixed number of arguments (as far as I know, anyway) it seems reasonable to expect .length should work on those.

(My current workaround is a mix of 1 & 2; I assign the function a length based on the FunctionAssignmentNode's params property. But that still has the deficiency mentioned for things like f=sin or f=atan2.

So anyway... In the spirit of #154, I definitely think it makes sense to add some introspection capabilities to the typed functions of this library. JS has pretty limited function introspection, but one of the things it does have is function.length. So IMO, if typed-function moves toward supporting introspection, it would make sense to support the JS standard (in addition to a cusotm API that reflects the richness of the library).

(And... again, I realize function.length is pretty limited, especially around things like rest parameters)

Hope that made sense; it was a bit more long-winded than I thought it would be.

[ChristopherChudzicki]

@josdejong Looking at #154 a bit more closely, I may have misunderstood it a bit. I will admit to not having looked too closely at typed-function before :embarrassed: . I probably could get the information I want from the keys of f.signatures.

Still, having a length property might make sense. The "conform to JS standard where possible, and provide extra APIs to express library richness" seems reasonable.

[josdejong]

Thanks for your inputs, your use cases help a lot.

1. About introspection of functions I think mathjs already has some very powerful options in this regard. Instead of evaluating a function, you can parse the function into an expression tree and inspect that with methods like transform and traverse. See docs https://mathjs.org/docs/expressions/expression_trees.html.

2. About compile time validation The cases you mention are two different cases of expressions that are valid from a syntax point of view, but invalid when trying to evaluate. There are more categories of those, like trying to get a value out of a matrix at an index that is out of bounds, or requiring a square matrix in certain functions, or requiring an integer number, etc. Some of these cases can be statically analyzed without being executed for real, but for others it would be a huge amount of work. About your specific cases:

1. Undefined symbol math.evaluate("f(x, y) = x^2 + y^2 + a") . Yeah, this can work a bit odd in mathjs. The variables are not resolved at the moment you define the function but when you actually evaluate the function, so:

   const scope = {}
   math.evaluate("f(x, y) = x^2 + y^2 + a", scope) // ok
   math.evaluate("f(2, 3)", scope) //  Error: Undefined symbol a
   scope.a = 42
   math.evaluate("f(2, 3)", scope) // 55 
   

2. Unexpected type of argument in function pow math.evaluate("f(x) = 2^[x,x,x]"). There are an infinite number of variations of this issue, where an argument for an operator or function is of the wrong type or size or range or something like that. I can imagine that it is possible to verify the argument types against the typed-function definitions, that would be interesting to try out. It will not solve all issues though: that would require pulling out all exceptions that any function can throw into some validation package which can "dry run" every possible expression, I don't think that is a possibility.