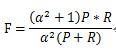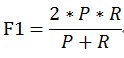deeplearning-cv-notes icon indicating copy to clipboard operation
deeplearning-cv-notes copied to clipboard

Published 20 hours ago • verified publisher icon jayboxyz

语义分割中的 Loss、评价指标

Open jayboxyz opened this issue 5 years ago • 5 comments

个人梳理

一、语义分割评价

交并比 IoU

指算法检测到的建筑物与真实的正像素的交集以及它们之间的比值。IoU 一般作为目标检测和语义分割中的最常用指标。

准确率 Precision 和 召回率 Recall

  • 准确率：指算法检测到的建筑物像素中真实正像素的百分比。
  • 召回率：即算法检测到正确建筑物占地面真实正像素的百分比。

如上，假设黄色区域即 S1 为建筑，红色区域即 S2 为预测，S3 为重叠区域，即预测正确的区域。那么：

  1. 准确率：Precision = S3/S2
  2. 召回率：Recall = S3/S1
  3. IoU 计算：IoU = s3/(s1+s2-s3) 另外也可以根据混淆矩阵计算得来。

混淆矩阵

参考：

- True Positive(真正, TP)：将正类预测为正类数. 
- True Negative(真负 , TN)：将负类预测为负类数. 
- False Positive(假正, FP)：将负类预测为正类数 → 误报 (Type I error). 
- False Negative(假负 , FN)：将正类预测为负类数 →漏报 (Type II error).

这篇文章推荐下：【错误率、精度、查准率、查全率和F1度量】详细介绍

jayboxyz avatar Nov 10 '19 15:11 jayboxyz

分割 Loss

几种分割loss

1、2d交叉熵（mutil class 分割）

def cross_entropy2d(input, target, weight=None, size_average=True):
    # input: (n, c, h, w), target: (n, h, w)
    n, c, h, w = input.size()
    # log_p: (n, c, h, w)
    if LooseVersion(torch.__version__) < LooseVersion('0.3'):
        # ==0.2.X
        log_p = F.log_softmax(input)
    else:
        # >=0.3
        log_p = F.log_softmax(input, dim=1)
    # log_p: (n*h*w, c)
    log_p = log_p.transpose(1, 2).transpose(2, 3).contiguous()
    log_p = log_p[target.view(n, h, w, 1).repeat(1, 1, 1, c) >= 0]
    log_p = log_p.view(-1, c)
    # target: (n*h*w,)
    mask = target >= 0
    target = target[mask]
    loss = F.nll_loss(log_p, target, weight=weight, size_average=False)
    if size_average:
        loss /= mask.data.sum()
    return loss

2、bce loss

            criterion = nn.BCELoss()
            y_pred = net(X)
            probs = F.sigmoid(y_pred)
            probs_flat = probs.view(-1)

            y_flat = y.view(-1)

            loss = criterion(probs_flat, y_flat.float())
            epoch_loss += loss.data[0]

            print('{0:.4f} --- loss: {1:.6f}'.format(i * batch_size / N_train,
                                                     loss.data[0]))

            optimizer.zero_grad()

            loss.backward()

            optimizer.step()

3、loss与bce叠加

        outputs = model(images)
        loss, bce_loss, soft_dice_loss = criterion(outputs, labels)
        loss_val = loss.data[0]
        sum_epoch_loss += loss_val
        if i == 0:
            optimizer.zero_grad()
        loss.backward()

4、bce和dice loss综合

def dice_loss(preds, trues, weight=None, is_average=True):
    num = preds.size(0)
    preds = preds.view(num, -1)
    trues = trues.view(num, -1)
    if weight is not None:
        w = torch.autograd.Variable(weight).view(num, -1)
        preds = preds * w
        trues = trues * w
    intersection = (preds * trues).sum(1)
    scores = 2. * (intersection + 1) / (preds.sum(1) + trues.sum(1) + 1)

    if is_average:
        score = scores.sum()/num
        return torch.clamp(score, 0., 1.)
    else:
        return scores

def dice_clamp(preds, trues, is_average=True):
    preds = torch.round(preds)
    return dice_loss(preds, trues, is_average=is_average)

class DiceLoss(nn.Module):
    def __init__(self, size_average=True):
        super().__init__()
        self.size_average = size_average

    def forward(self, input, target, weight=None):
        return 1-dice_loss(F.sigmoid(input), target, weight=weight, is_average=self.size_average)

class BCEDiceLoss(nn.Module):
    def __init__(self, size_average=True):
        super().__init__()
        self.size_average = size_average
        self.dice = DiceLoss(size_average=size_average)

    def forward(self, input, target, weight=None):
        return nn.modules.loss.BCEWithLogitsLoss(size_average=self.size_average, weight=weight)(input, target) + self.dice(input, target, weight=weight)

        ypreds = self.model(images)
        loss = self.criterion(ypreds, ytrues)

        ret['loss'] = loss.data
        for name, func in self.metrics:
            acc = func(F.sigmoid(ypreds)[:, :, 6:-6, 6:-6].contiguous(), ytrues[:, :, 6:-6, 6:-6].contiguous())
            ret[name] = acc.data
        if training:
            loss.backward()
            torch.nn.utils.clip_grad_norm(self.model.parameters(), 1.)

jayboxyz avatar Nov 10 '19 15:11 jayboxyz

图像分割-评价指标

深度学习之语义分割中的度量标准（准确度）(pixel accuracy, mean accuracy, mean IU, frequency weighted IU)

参考：https://blog.csdn.net/majinlei121/article/details/78965435

纠正：该文的 FWIoU 表达式有误，正确表达式参考这个：https://github.com/martinkersner/py_img_seg_eval#frequency-weighted-iu Frequency Weighted IU： image

image

jayboxyz avatar Nov 10 '19 15:11 jayboxyz

评价指标

From 论文《基于深度学习的图像分割研究_张明月》

  • 交叉联合度量：IoU
  • 平均交叉联合度量：mIoU
  • 全局正确率：全局正确率（global accuracy）被定义为测试集上所有分割结果（Prediction）的像 素点的集合 P 与标注结果（Ground Truth）的像素集合 GT 之间的交集的像素数比上测 试集总的像素点的数量 M，具体公式如下。全局正确率衡量了像素级分割算法在分类预测上的总体表现。
  • 分类平均正确率：在定义分类平均正确率（class average accuracy）之前先定义分类正确率，分类正确率是用来评价像素级分割中对每个分类分割效果的指标，具体公式如下：

From 《语义分割-从入门到放弃》

  • 数据问题：分割不像检测等任务，只需要标注一个bbs就可以拿来使用，分割需要精确的像素级标注，包括每一个目标的轮廓等信息；

  • 计算资源问题：个人觉得太吃backbone，这就说明了如果要想得到较高的精度就需要使用类似于ResNet101等深网络。同时，分割预测了每一个像素，这就要求feature map的分辨率尽可能的高，这都说明了计算资源的问题，加GPUGPUGPU.....，虽然也有一些轻量级的网络，但精度还是太低了，期待类似于YOLO/SSD这样的工作能在分割中出现；

  • 精细分割：查看cityscape结果可以看出，很多算法的像道路、建筑物等类别，分割精度很高，能达到98%，而对于细小的类别，像行人、交通等等，由于其轮廓太小，而无法精确的定位轮廓，造成精度较低；

  • 上下文信息：分割中上下文信息很重要，否则会造成一个目标被分成多个part，或者不同类别目标分类成相同类别；

  • mIoU:这个指标是应用最多的，也是目前排名分割算法的依据。IoU就是每一个类别的交集与并集之比，而mIoU则是所有类别的平均IoU。论文均使用这一指标比较。

  • speed:由于有些分割算法是针对实时语义分割设计的，所以速度也是一个很重要的评价指标，当然评价速度需要公平比较，包括使用的图像大小、电脑配置一致。

  • 当然还有其他指标，如pixel accuracy、mean accuraccy等。

下面以一个简单的例子，说明怎么计算mIoU，由于分割也是分类问题，分类问题的指标一般使用混淆矩阵来求解。

mIoU:

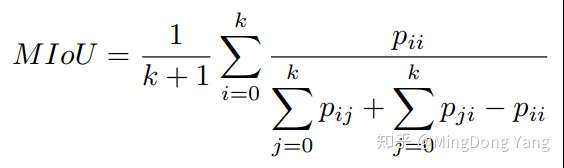
其中(k+1)为类别数，pii表示TP，pij表示FN，pji表示FP（i表示真实类别，j表示其他类别），则每一个类别的IoU可以看作，IoU=TP/(TP+FN+FP).

以三个类别为例，如下是一个混淆矩阵：

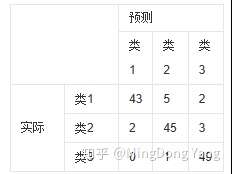
对于

  • 类别1：TP=43，FN=7，FP=2；
  • 类别2：TP=45，FN=5，FP=6；类别3：TP=49，FN=1，FP=5.
  • 因此：IoU1=43/(43+2+7)=82.69%，IoU2=45/(45+5+6)=80.36%，IoU=49/(49+1+5)=89.09%，
  • 因此mIoU=84.05%.其实就是矩阵的每一行加每一列，再减去重复的TP。

From 15.评价指标 - 简书

召回率 （Recall）、准确率（Precision）、漏检率（Missing Alarm）和错检率（False Alarm） 以及 综合评价指标 F-Measure ——见：《基于改进的全卷积神经网络 高分遥感数据语义分割研究》：

1-1. 精确率与召回率

精确率（Precision）指的是模型判为正的所有样本中有多少是真正的正样本；召回率（Recall）指的是所有正样本有多少被模型判为正样本，即召回。感觉精确率是个局部的，召回率是个全局的。

1-2. ROC

真正类率(true positive rate ,TPR)，刻画的是分类器所识别出的 正实例占所有正实例的比例（正样本预测结果数 / 正样本实际数）。负正类率(false positive rate, FPR)，计算的是分类器错认为正类的负实例占所有负实例的比例（被预测为正的负样本结果数 /负样本实际数）。 ( TPR=0,FPR=0 ) 把每个实例都预测为负类的模型 ( TPR=1,FPR=1 ) 把每个实例都预测为正类的模型 ( TPR=1,FPR=0 ) 理想模型

ROC曲线下方的面积（Area Under the ROC Curve, AUC）提供了评价模型平均性能的另一种方法。如果模型是完美的，那么它的AUC = 1，如果模型是个简单的随机猜测模型，那么它的AUC = 0.5，如果一个模型好于另一个，则它的曲线下方面积相对较大。

首先AUC值是一个概率值，当你随机挑选一个正样本以及一个负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。当然，AUC值越大，当前的分类算法越有可能将正样本排在负样本前面，即能够更好的分类。

From 4.4.2分类模型评判指标（一） - 混淆矩阵(Confusion Matrix)

因此，我们就能得到这样四个基础指标，我称他们是一级指标（最底层的）：

  • 真实值是positive，模型认为是positive的数量（True Positive=TP）
  • 真实值是positive，模型认为是negative的数量（False Negative=FN）：这就是统计学上的第一类错误（Type I Error）
  • 真实值是negative，模型认为是positive的数量（False Positive=FP）：这就是统计学上的第二类错误（Type II Error）
  • 真实值是negative，模型认为是negative的数量（True Negative=TN）

将这四个指标一起呈现在表格中，就能得到如下这样一个矩阵，我们称它为混淆矩阵（Confusion Matrix）：

。。。

二级指标

但是，混淆矩阵里面统计的是个数，有时候面对大量的数据，光凭算个数，很难衡量模型的优劣。因此混淆矩阵在基本的统计结果上又延伸了如下4个指标，我称他们是二级指标（通过最底层指标加减乘除得到的）：

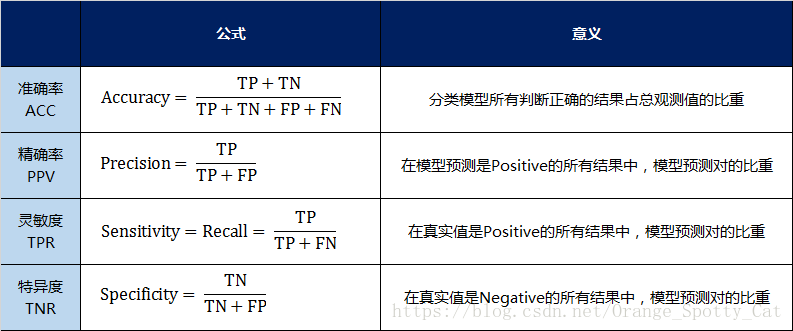
  • 准确率（Accuracy）—— 针对整个模型
  • 精确率（Precision）
  • 灵敏度（Sensitivity）：就是召回率（Recall）
  • 特异度（Specificity）

我用表格的方式将这四种指标的定义、计算、理解进行了汇总：

通过上面的四个二级指标，可以将混淆矩阵中数量的结果转化为0-1之间的比率。便于进行标准化的衡量。

在这四个指标的基础上在进行拓展，会产令另外一个三级指标

三级指标

这个指标叫做F1 Score。他的计算公式是：

其中，P代表Precision，R代表Recall。

F1-Score指标综合了Precision与Recall的产出的结果。F1-Score的取值范围从0到1的，1代表模型的输出最好，0代表模型的输出结果最差。

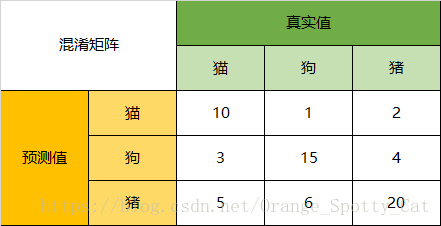
Accuracy

在总共66个动物中，我们一共预测对了10 + 15 + 20=45个样本，所以准确率（Accuracy）=45/66 = 68.2%。

以猫为例，我们可以将上面的图合并为二分问题：

Precision

所以，以猫为例，模型的结果告诉我们，66只动物里有13只是猫，但是其实这13只猫只有10只预测对了。模型认为是猫的13只动物里，有1条狗，两只猪。所以，Precision（猫）= 10/13 = 76.9%

Recall

以猫为例，在总共18只真猫中，我们的模型认为里面只有10只是猫，剩下的3只是狗，5只都是猪。这5只八成是橘猫，能理解。所以，Recall（猫）= 10/18 = 55.6%

Specificity

以猫为例，在总共48只不是猫的动物中，模型认为有45只不是猫。所以，Specificity（猫）= 45/48 = 93.8%。

虽然在45只动物里，模型依然认为错判了6只狗与4只猫，但是从猫的角度而言，模型的判断是没有错的。

（这里是参见了Wikipedia，Confusion Matrix的解释,https://en.wikipedia.org/wiki/Confusion_matrix）

F1-Score

通过公式，可以计算出，对猫而言，F1-Score=（2 * 0.769 *  0.556）/（ 0.769 +  0.556） = 64.54%

同样，我们也可以分别计算猪与狗各自的二级指标与三级指标值。

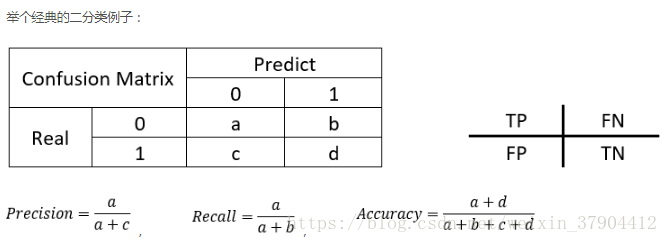
根据分类器在测试数据集上的预测或正确或不正确可以分为四种情况：

  • TP——将正类预测为正类数
  • FN——将正类预测为负类数
  • FP——将负类预测为正类数
  • TN——将负类预测为负类数

记忆方法： T=True=+1 F=False=-1 （T和N并不是指代实际的是正类和负类） P=Positive=+1 N=Negative=-1 （P和N指明了预测的是正类还是负类） 实际正例=+1 实际负例=-1

实际的正类和负类按照下面的方法：

  • TP的实际类别 = 1*1=1（实际正例）
  • FN的实际类别=-1*-1=1（实际正例）
  • FP的实际类别=-1*1=-1（实际负例）
  • TN的实际类别=1*-1=-1（实际负例）

因此：

  • TP+FN=实际正例的数量
  • TP+FP=预测正例的数量

。。。

——from：https://blog.csdn.net/weixin_37904412/article/details/80554199

2、综合评价指标（F-Measure）

P和R指标有时候会出现的矛盾的情况，这样就需要综合考虑他们，最常见的方法就是F-Measure（又称为F-Score）。

F-Measure是Precision和Recall加权调和平均：

当参数α=1时，就是最常见的F1，也即

可知F1综合了P和R的结果，当F1较高时则能说明试验方法比较有效。

个人补充：

当 \beta =1时，成为F1-Score，这时召回率和精确率都很重要，权重相同。当有些情况下我们认为精确率更为重要，那就调整 β 的值小于 1 ，如果我们认为召回率更加重要，那就调整 β的值大于1，比如F2-Score。

举个例子：

癌症检查数据样本有10000个，其中10个是有癌症的样本。假设无癌症的9900个样本中预测正确了9980个，在10个癌症数据中预测正确了9个，此时：

  • Accuracy = (9+9980)/10000 = 99.89%
  • Precision = 9/(9 + 10) = 47.36%
  • Recall = 9 / 10 = 90%
  • F1-score = 2 x (47.36% x 90%)/(1 x 47.36% + 90%)
  • F2-score = 2 x (47.36% x 90%)/(4 x 47.36% + 90%)

——from：深度学习F2-Score及其他(F-Score)

kappa 系数

——from：https://blog.csdn.net/xtingjie/article/details/72803029

Kappa系数用于一致性检验，也可以用于衡量分类精度。kappa系数的计算是基于混淆矩阵的

kappa计算结果为-1~1，但通常kappa是落在 0~1 间，可分为五组来表示不同级别的一致性：0.0~0.20极低的一致性(slight)、0.21~0.40一般的一致性(fair)、0.41~0.60 中等的一致性(moderate)、0.61~0.80 高度的一致性(substantial)和0.81~1几乎完全一致(almost perfect)。

上图就是个混淆矩阵

Jaccard系数

Jaccard系数与Jaccard距离：https://blog.csdn.net/qq_26710805/article/details/79855226

——from：https://www.jianshu.com/p/b5996bf06bd6

jayboxyz avatar Nov 11 '19 05:11 jayboxyz

图像语义分割准确率度量方法总结

——from：https://zhuanlan.zhihu.com/p/38236530

衡量图像语义分割准确率主要有三种方法：

像素准确率（pixel accuracy, PA） 平均像素准确率（mean pixel accuracy, MPA） 平均IOU（Mean Intersection over Union, MIOU ） 在介绍三种方法之前，需要先说明一些符号表示的意义。

k ：类别总数，如果包括背景的话就是 k+1

p_{ij} ：真实像素类别为 i 的像素被预测为类别 j 的总数量，换句话说，就是对于类别为 i 的像素来说，被错分成类别 j 的数量有多少。

P_{ii} ：真实像素类别为 i 的像素被预测为类别 i 的总数量，换句话说，就是对于真实类别为 i 的像素来说，分对的像素总数有多少。

1.PA

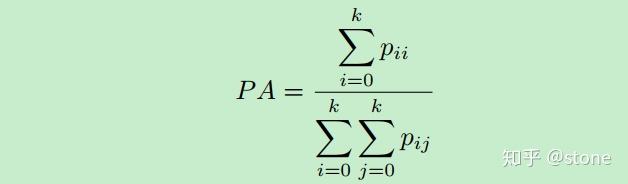
2.MPA

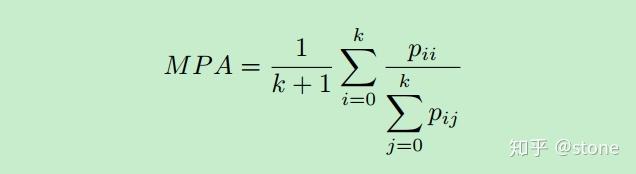
3.MIoU

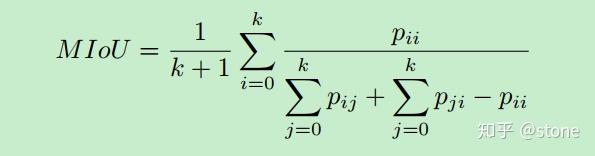
jayboxyz avatar Nov 11 '19 05:11 jayboxyz

From 遥感分类精度评价方法--混淆矩阵和kappa系数

遥感影像分类之后需要进行分类精度评价，精度评价方法中最常见的就是混淆矩阵和kappa系数。现把指标列举如下:

混淆矩阵（confusion matrix）

误差矩阵（error matrix）又称混淆矩阵（confusion matrix），是一个用于表示分为某一类别的像元个数与地面检验为该类别数的比较阵列。通常，阵列中的列代表参考数据，行代表由遥感数据分类得到的类别数据。有像元数和百分比表示两种。

总体分类精度（Overall Accuracy）

等于被正确分类的像元总和除以总像元数。被正确分类的像元数目沿着混淆矩阵的对角线分布，总像元数等于所有真实参考源的像元总数

Kappa系数（Kappa Coefficient）

它是通过把所有真实参考的像元总数（N）乘以混淆矩阵对角线（XKK）的和，再减去各类中真实参考像元数与该类中被分类像元总数之积之后，再除以像元总数的平方减去各类中真实参考像元总数与该类中被分类像元总数之积对所有类别求和的结果。

错分误差(Commission Error)

指被分为用户感兴趣的类，而实际上属于另一类的像元，错分误差显示在混淆矩阵的行里面。

漏分误差（Omission Error）

指本属于地表真实分类，但没有被分类器分到相应类别中的像元数。漏分误差显示在混淆矩阵的列里。

制图精度（Producer’s Accuracy）

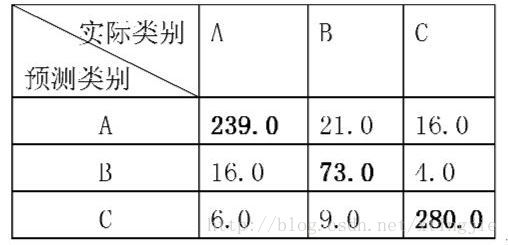
制图精度或生产者精度是指分类器将整个影像的像元正确分为A类的像元数（对角线值）与A类真实参考总数（混淆矩阵中A类列的总和）的比率。

用户精度（User’s Accuracy）

是指正确分到A类的像元总数（对角线值）与分类器将整个影像的像元分为A类的像元总数（混淆矩阵中A类行的总和）比率。

jayboxyz avatar Nov 11 '19 05:11 jayboxyz