Class specificity of attribution maps of embedding based classifiers

[AshAswin]

Dear Authors,

Thanks for sharing the great repository.

This is a question about generating attribution maps for embedding CNNs. Please refer to the attachment for the context. 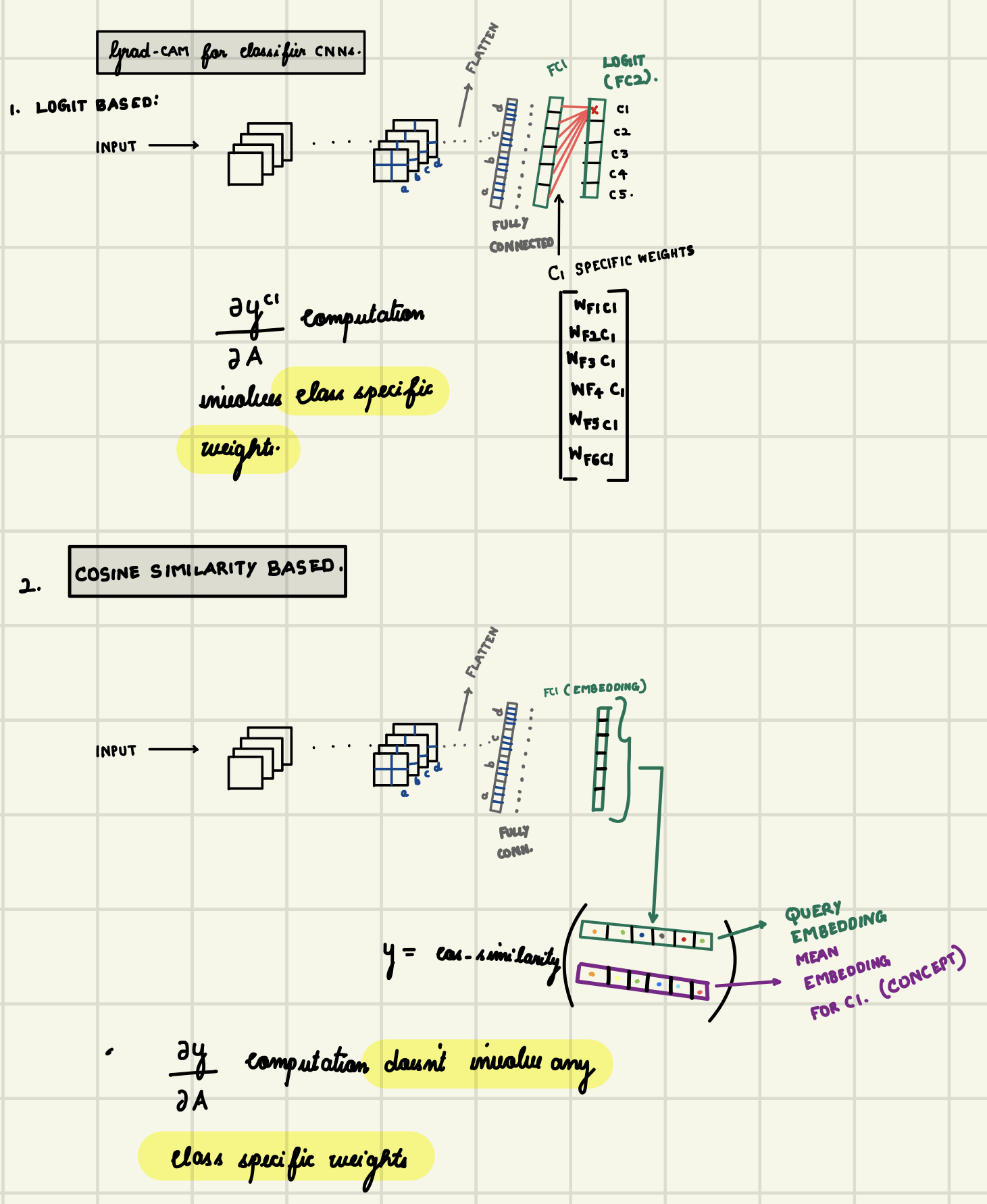For applying Grad-CAM to vanilla classification CNNs, we compute gradients of the logit (y ^c1) of the target class (c1) with respect to feature maps (A) of the chosen convolutional layer. The gradient thus computed is affected by parameters specific to c1 (W _F*c1 ). (Present between FC1 and FC2(logit layer) in the given image).

However, in the case of embedding-based attribution(Cosine Similarity Based), we compute gradients of the cosine similarity score (y) with respect to feature maps, which is not affected by any class-specific parameters. (.i.e. connections in an embedding network are not class specific).

1. "How do attribution maps obtained using the latter remain class-specific (discriminative) in spite of the above-mentioned fact"?

If we use the mean embedding of a target class's train instances as the concept and compute its similarity with embedding of a test instance,

2. Does its attribution map illustrate the presence/projection of the target class's concept in the test instance?

3. How does the attribution map referred to in the previous question, differ from the one generated with the help of logits in vanilla CNNs? I assume the difference would be caused by the absence of parameters in FC2, and the assumption of taking the mean of training instances as a reference embedding.

[jacobgil]

Hi,

1. They are not class specific any more, because the classifier part is actually discarded when we keep only the embedding part. Instead of being "class" specific, they are being "query embedding" specific and just try to explain the similarity to the embedding.

2. Yes.

3. Yes, instead of taking the dot product of the embedding with FC2, we would take the (normalized) dot product with the mean embedding. I think we could however interpret the fully connected layer column for that category, as a "concept" for that category, but just something learnable instead of being computed as a mean embedding,