hyperplay

Explore tilings on the hyperbolic plane

PLAY HERE!

(Or, if you are feeling adventurous, you can play the advanced version here. Look on the wiki for some interesting starting points. I've also made some interactive demonstration of the concepts involved: generalized stereographic projection, projection and mirroring, projection onto the 2D plane with curved edges )

Usage:

To start with it shows the {3,q} family of tilings, and intermediate forms.

Move the mouse left and right to change the curvature of space. Negative curvature gives us hyperbolic tilings. Zero curvature gives us plane tiling. Positive curvature gives us polyhedra.

Use the + and - buttons to change the number of sides in the base polygon.

What the heck am I looking at?

Notice that there's a triangle in the center that never changes. We will use the edges of this triangle as mirrors.

First we reflect the triangle in each of those mirrors. Our triangle has now got three more triangles around it, one fixed to each edge.

We repeat this process again and again. We end up with lots of triangles, all joined edge to edge.

At some values of curvature the triangles all overlap neatly and we get a nice tiling. This can be a flat tiling like you could use in your bathroom, or it could lie in a curved space like on a ball. A tiled ball is a polyhedron of course.

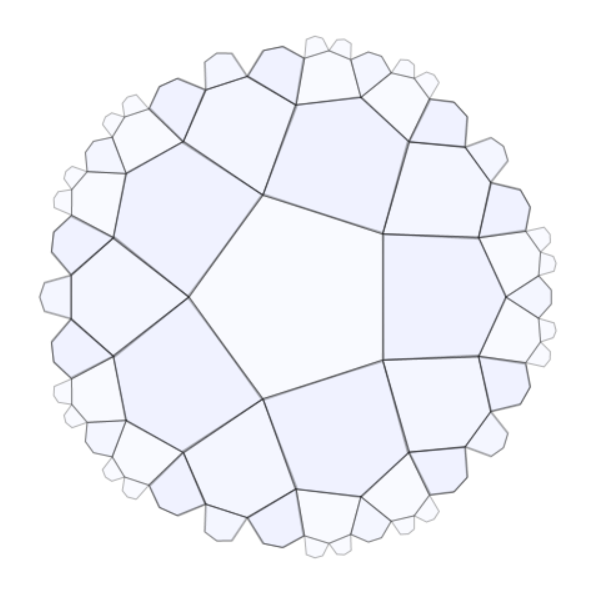
One nice thing about making tilings like this (Wythoff Construction) is that we can do the same thing in negatively curved (hyperbolic) space to get the hyperbolic tilings like {5,4} shown above. We render these with the Poincaré disk model which is why the pentagons get small and stretched towards the outside.

Credits:

Thanks to Adam P. Goucher for getting me started with hyperbolic tessellation! Here's a blog post he wrote about it.

He made his own interactive demonstration of Wythoff Construction, here.

Discussions:

• Comments on the original Google+ post.
• The Aperiodical
• Hacker News