radis

radis copied to clipboard

🎯 Todo

Note: the most recent GPU update had a bug in the determination of the Lorentzian envelopes [details below], producing erroneous equilibrium spectra when using GPU. This will be solved in an upcoming PR, but is already available here.

With the LDM approach, it is important to determine the min/max values of the Gaussian and Lorentzian widths, as they determine the gridsize and -spacing. Of course, this determination should not become a bottleneck.

For large line-lists, calculating the G&L widths first, then checking their min/max values can become very slow. Moreover, for a GPU or other parallel computation it's a bit involved to determine an absolute maximum/minimum so a better way would be preferable; RADIS already has this for the GPU implementation.

The calculation of the Gaussian widths are relatively straightforward: log_wG = log_2vMm + hlog_T

with: log_2vMm = np.log(2*v0) + 0.5*np.log(2*k*np.log(2)/(c**2*Mm)) hlog_T = 0.5*np.log(T)

and: v0 = line position (vacuum wavenumber) k = Boltzmann constant c = speed of light in vacuum Mm = molecular mass T = temperature

By working with logarithms of our quantities, we see that the temperature only causes a constant offset. This means we can determine once, in advance, the min/max values of log_2vMm, and then calculate the min/max values of log_wG by adding hlog_T to those.

The Lorentzian widths are more complicated, since they are a function of temperature and pressure: log_2gs + log_p + na*log_rT

with: log_2gs = np.log(2*gs) log_p = np.log(p) log_rT = np.log(296./T)

and: gs = self-broadening half-width p = pressure (bar) T = temperature In order to quickly calculate the min/max Lorentzian widths, the GPU implementation first determines what lines could be possible candidates for the min or maximum pressure, by looking at their values of na (slope) and log_2gs (offset). Below a figure with a number of these lines for a realistic database:

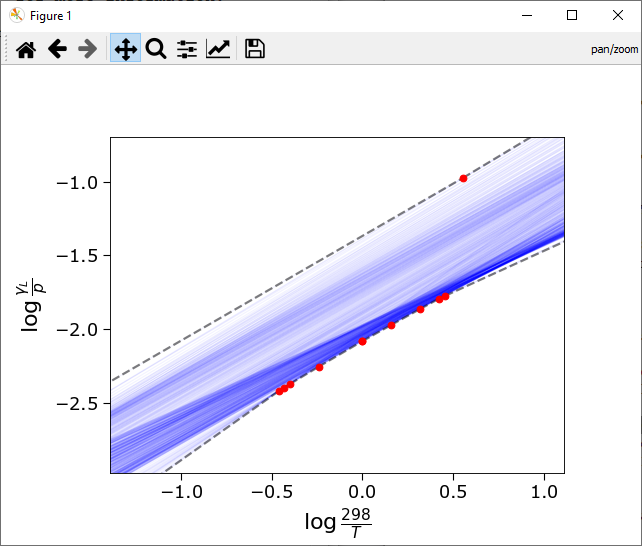
I call the intersection of lines at the top and bottom, highlighted by the black dashed lines, the top- and bottom envelopes. Once the temperature and pressure information is available, they can be used to calculate the min/max L-width very quickly.

Determining the top and bottom envelopes is somewhat slow and takes up to a couple of seconds for database sizes relevant to GPU computations (100M+), but calculating the min/max width once the envelopes are known is lightning fast. In the example figure above, the red dots indicate intersections at which temperature the min/max value is determined by a different spectral line. The code thus has to evaluate only a handful of these numbers.

💡 Possible implementations

So far everything I described is already implemented, but not in the right place. It is currently part of the GPU initialization (radis/lbl/gpu.py) and the envelopes are stored in separate cache files.

It would be better if these envelopes (as well as finding the min/max log_2vMm values for the G-widths) were calculated at the moment the database is cached, since as long as the database doesn't change these values won't change either. Moreover, these could be useful for CPU computations as well, underlining they should not be in the GPU specific module.

---

_{Tip : you can vote for New Features on https://feathub.com/radis/radis}

@dcmvdbekerom is the bug on Lorentzian enveloppes on the released version 0.9.29, or only on the develop branch? In the former case we'll release 0.9.30 a bit earlier!

The bug was introduced in https://github.com/radis/radis/pull/266, I think that one only made it to the development branch.

Yes, that was 7 days ago, so definitely only the develop branch was impacted. Congrats for finding it!

Thanks! But to be fair it was me who messed it up in the first place 😅

There is still an inconsistency between gpu and CPU of about 5% or so which I believe we had already during the gsoc (@pkj-m); I'm hoping this is due to the fact self broadening isn't implemented yet.

An easy way to check is to compare for mole fractions of a few ppm.