fucking-algorithm
 fucking-algorithm copied to clipboard
fucking-algorithm copied to clipboard
归并排序详解及应用 :: labuladong的算法小抄
好难
493 翻转对题目中 对merge函数的改造代码里:
// 在合并有序数组之前,加点私货
for (int i = lo; i <= mid; i++) {
// 对于左半边的每个 nums[i],都去右半边寻找符合条件的元素
for (int j = mid + 1; j <= hi; k++) {
// nums 中的元素可能较大,乘 2 可能溢出,所以转化成 long
if ((long)nums[j] > (long)nums[j] * 2) {
count++;
}
}
}
if ((long)nums[j] > (long)nums[j] * 2) 应改为:if ((long)nums[i] > (long)nums[j] * 2)
@zzp-seeker 已修正,感谢指出~
东哥,文中有个sort, 误打成 srot了
@MathsGo 感谢指出,已修正~
// 进行效率优化,维护左闭右开区间 [mid+1, end) 中的元素乘 2 小于 nums[i]
这里的效率优化同样是双层嵌套,for + while 为什么这样就不超时了?
人都看傻了
@yuanzhixiang while 里面j不会回退,相当于O(N)复杂度,而for循环j会回退的相当于O(N^2)
那么计算区间和 S(i, j) 只需要用 preSum[j] - preSum[i] 就可以计算出来。
感觉这里表述并不是十分严谨
preSum[j] - preSum[i] 对于 nums 数组来说,对应的是 (i, j] 区间的区间和
而题中所给的区间和 S(i, j) 的定义是包含 i 和 j 的
@wy-luke 你说的有道理,我改下表述
有个地方没想明白,
lower <= preSum[j] - preSum[i] <= upper
这里的 upper > 0 意味着 preSum[j] > preSum[i] ,那 [start, end) 应该也有可能在左侧区间吧?为啥 start 还是从 mid+1 开始的
贴一个cpp版本:315. 计算右侧小于当前元素的个数
class Solution
{
public:
vector<int> countSmaller(vector<int> &nums)
{
int n = nums.size();
arr.resize(n);
for (int i = 0; i < n; i++)
arr[i] = new Pair(nums[i], i);
// 执行归并排序,本题结果被记录在count中
count.resize(n, 0);
tmp.resize(n);
mergeSort(arr, 0, n - 1);
return count;
}
private:
struct Pair
{
int val, id;
Pair() : val(0), id(0){};
Pair(int val, int id) : val(val), id(id){};
};
vector<Pair *> arr;
vector<Pair *> tmp; // 归并排序所用的辅助数组
vector<int> count; // 记录每个元素后面比自己小的元素个数
// 归并排序
void mergeSort(vector<Pair *> &arr, int left, int right)
{
if (left >= right)
return;
// 归并划分
int mid = (left + right) / 2;
// 归并排序左右子数组
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
// 将两部分有序数组合并为一个有序数组
for (int k = left; k <= right; k++)
tmp[k] = arr[k];
int i = left, j = mid + 1; // 两个指针分别指向左/右子数组的首个元素
for (int k = left; k <= right; k++)
{
if (i == mid + 1)
arr[k] = tmp[j++];
else if (j == right + 1 || tmp[i]->val <= tmp[j]->val)
{
arr[k] = tmp[i++];
// 更新count数组
count[arr[k]->id] += j - mid - 1;
}
else
{
arr[k] = tmp[j++];
// 更新count数组
// count[arr[k]->id] += j - mid - 1;
}
}
}
};
@zhyozhi 你的理解是对的,但让 start 从 mid + 1 开始不是基于谁大谁小的原因,而是基于归并排序的原理。每次递归处理半个数组,谁都不要多管闲事,否则无法保证不会多算/漏算。
493.翻转对 javascript version
var reversePairs = function(nums) {
// 用于辅助合并有序数组
let temp = new Array(nums.length);
let count = 0;
// 定义 将子数组nums[left...right]进行排序
function sortNums(nums, left, right) {
// base case
if (left >= right) {
return;
}
// 防止溢出
let mid = Math.floor(left + (right - left) / 2);
// 先对左半部分数组nums[left...mid]排序
sortNums(nums, left, mid);
// 再对右半部分数组nums[mid+1...right]排序
sortNums(nums, mid + 1, right);
// 将两部分有序数组合并成一个有序数组
merge(nums, left, mid, right);
}
// 定义 将nums[left...mid]和nums[mid+1...right]这两个有序数组合并成一个有序数组
function merge(nums, left, mid, right) {
// 先把nums[left...right]复制到辅助数组中
// 以便合并后的结果能够直接存入nums
for (let n = left; n <= right; n++) {
temp[n] = nums[n];
}
// 在合并有序数组之前,加点私货
let m = left, n = mid + 1;
while (m <= mid ) {
// 对左半边的nums[m] 寻找符合条件的最大n值
while (n <= right && nums[m] > 2 * nums[n]) {
n++;
}
// 符合条件的元素个数等于n到mid-1之间的距离
count += n - mid -1;
m++;
};
// 数组双指针技巧 合并两个有序数组
let i = left, j = mid + 1;
for (let p = left; p <= right; p++) {
if (i == mid + 1){
// 左半边数组已全部被合并
nums[p] = temp[j++];
} else if (j == right + 1) {
// 右半边数组已全部被合并
nums[p] = temp[i++];
} else if (temp[i] < temp[j]) {
nums[p] = temp[i++];
} else if (temp[i] >= temp[j]) {
nums[p] = temp[j++];
}
}
}
// 排序整个数组(原地修改)
sortNums(nums, 0, nums.length - 1);
return count;
};
315有些不明白,如果用Pair记录元素位置,那么题目如果给出了有重的test case数组,要怎么处理呢?
327 关于私活滑动窗口部分的理解画的图 ~~也可能理解错了~~ 😄 😢
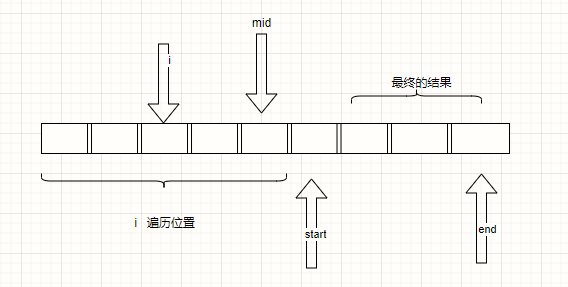
人傻了,想不到,呜呜呜
@zhongweiLeex 优秀👍
493题未优化双层 for 那里,内层 for 的 j++ 写成了 k++
@PiggyJake 感谢指出,已修复
求问一下题目327:区间和的个数,前缀和lower<=presum[j]-presum[i]<=upper肯定得要求i< j吧?但是归并排序中在左数组中的前缀和下标不一定比右数组大吧?这样怎么能保证i<j呢?
315.c++
```c++
class Solution {
private:
class Pair {
public:
int val, id;
Pair(int val, int id) {
this->val = val;
this->id = id;
}
//这个默认构造函数很关键
Pair () : val(0), id(0) {}
};
vector<Pair> temp;
vector<int> count;
private:
void sort(vector<Pair>& arr, int lo, int hi) {
if (lo == hi) {
return;
}
int mid = lo + (hi - lo) / 2;
sort(arr, lo, mid);
sort(arr, mid + 1, hi);
merge(arr, lo, mid, hi);
}
void merge(vector<Pair>& arr, int lo, int mid, int hi) {
for (int i = lo; i <= hi; i++) {
temp[i] = arr[i];
}
int i = lo, j = mid + 1;
for (int p = lo; p <= hi; p++) {
if (i == mid + 1) {
arr[p] = temp[j++];
} else if (j == hi + 1) {
arr[p] = temp[i++];
count[arr[p].id] += j - mid - 1;
} else if (temp[i].val > temp[j].val) {
arr[p] = temp[j++];
} else {
arr[p] = temp[i++];
count[arr[p].id] += j - mid - 1;
}
}
}
public:
vector<int> countSmaller(vector<int>& nums) {
int n = nums.size();
count.resize(n);
temp.resize(n);
vector<Pair> arr(n);
for (int i = 0; i < n; i++) {
arr[i] = {nums[i], i};
}
sort(arr, 0, n - 1);
vector<int> res;
for (int n : count) {
res.push_back(n);
}
return res;
}
};
求二叉树最大深度这里:因为求二叉树最大深度的操作代码其实既可以写在后序位置也可以写在前序位置,我个人认为写在前序位置是求深度,而写在后序位置是求高度的。 因为若是写在后序位置,等于先一条道走到底,这时才返回叶子结点的'深度'为1,而这是不符合逻辑的。
// 定义:输入根节点,返回这棵二叉树的最大深度
int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
// 利用定义,计算左右子树的最大深度
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
// 整棵树的最大深度等于左右子树的最大深度取最大值,
// 然后再加上根节点自己
int res = Math.max(leftMax, rightMax) + 1;
return res;
}
小前端提问,merge合并的时候,判断条件的顺序不同结果也不同了...看样子最后一层else的temp[i] <= temp[j]必须放在最后面,我是按照下面写的,结果出了问题😂,有人替我解惑一下嘛?
if (temp[i] > temp[j]) {
nums[p] = temp[j++]
} else if (temp[i] <= temp[j]) {
nums[p] = temp[i++]
} else if (i === mid + 1) {
nums[p] = temp[j++]
} else if (j === r + 1) {
nums[p] = temp[i++]
}
大致明白了,j可能已经越界了。。
@Matilda-Yxx 这里我想没想明白
东哥,315. 计算右侧小于当前元素的个数 这个例题中的temp数组中 mid 为什么在值为 5 的位置,而不是值为 2 的位置
好吧!我知道了,合并的两边应该时有序的
前面都能理解,可是327题就完全不懂了。搞不懂为什么要在mergesort的基础上做。我也不知道我为啥在纠结一点,比如,preSum排序前preSum[5]-preSum[1]与排序后preSum[5]-preSum[1]的区间和是不一样的啊。
为什么不直接用hashmap,而要创造一个内部类