LoopVectorization.jl

LoopVectorization.jl copied to clipboard

This is a fantastic package. I've discovered that it, like Julia in general, comes with a hidden cost, "time to first plot." My package currently uses @tturbo in half a dozen utility functions, such as for computing columnwise dot products of two wide matrices. @tturbo speeds these up. But it adds greatly to latency, to the point where that I worry that it will repel users. The package is a statistical tool. If we want Julia to be used interactively like R for statistics, or even for fast Julia-based packages to be used via connectors in R and Python, I think people will not want to have to wait 30 seconds for each tool they load in each session.

I'm just wondering if there's anything I can do now to minimize the tradeoff in using LoopVectorization.

I have applied SnoopCompile and striven to follow the advice of @timholy in its documentation. Here is the summarized output from a SnoopCompile result called tinf when I don't use LoopVectorization, and call my package for the first time in a session:

julia> tinf
InferenceTimingNode: 14.882703/16.869373 on Core.Compiler.Timings.ROOT() with 139 direct children

And here it is when I do use @tturbo in the package:

julia> tinf
InferenceTimingNode: 18.754393/28.590440 on Core.Compiler.Timings.ROOT() with 261 direct children

If I understand right, without @tturbo, there's ~2 seconds of inference on first use and ~15 seconds (14.882703) of other stuff (for the displayed total of 16.869373). Using @tturbo adds ~8 seconds of inference and ~4 seconds of other stuff. The SnoopCompile flame graph of the latter is:

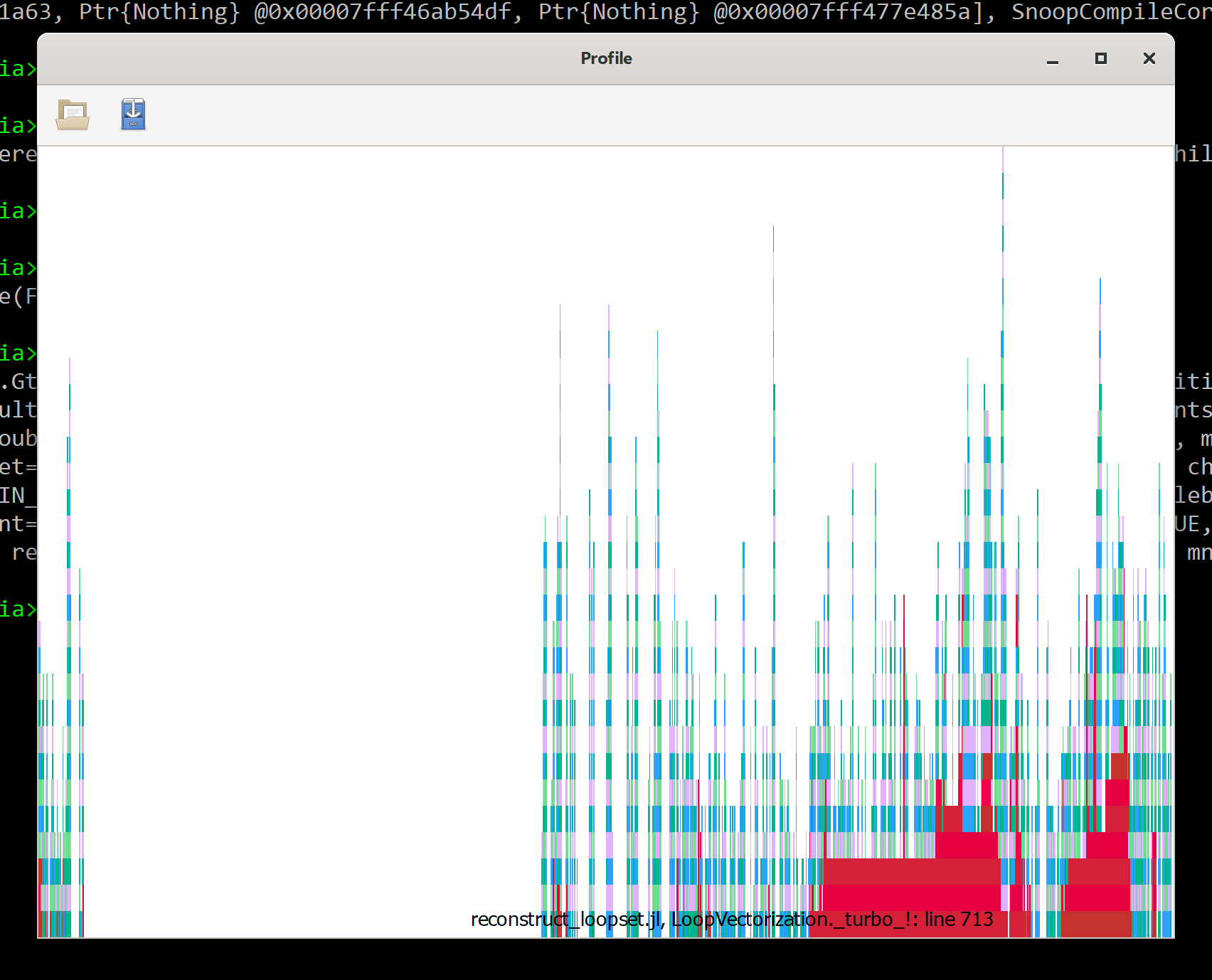
In case useful, here is a clean demo of what I'm experiencing, @tturbo creating a lot of latency despite the use of precompile():

using Pkg
Pkg.generate("TurboDemo")
Pkg.activate("TurboDemo")
Pkg.add("LoopVectorization")
Pkg.resolve()
Pkg.activate()
open("TurboDemo/src/TurboDemo.jl", "w") do io
  write(io, """
    module TurboDemo
    using LoopVectorization

    function coldot!(dest::Matrix{Float64}, A::Matrix{Float64}, B::Matrix{Float64})
      @tturbo for i ∈ eachindex(axes(A,2),axes(B,2)), j ∈ eachindex(axes(A,1),axes(B,1))
        dest[i] += A[j,i] * B[j,i]
      end
      nothing
    end

    precompile(coldot!, (Matrix{Float64}, Matrix{Float64}, Matrix{Float64}))
    end
  """)
end

push!(LOAD_PATH, "TurboDemo/")
using TurboDemo, SnoopCompileCore
A = rand(10,10000); B = rand(10,10000); dest = fill(0.,1,10000);
tinf = @snoopi_deep TurboDemo.coldot!(dest,A,B);
using SnoopCompile, ProfileView, Profile
tinf

I get:

InferenceTimingNode: 0.198680/9.662668 on Core.Compiler.Timings.ROOT() with 8 direct children

which I gather means close to 10 seconds of load-time inference. Thanks!

This is unfortunately a difficult issue, somewhat central to LoopVectorization's current design.

It should be largely addressed in the rewrite/redesign, but I can only work on that as my free time allows (unless some organization can pay me/Julia Computing for its development), so I cannot promise that this will happen within the next year.

Just curious--because I've been thinking about Julia and LoopVectorization and think it's all interesting. I imagine a big software stack running from metaprogramming and programming in Julia to all the lowering steps done by Julia to all the lowering steps done by LLVM; and somewhere down there near the bottom are math libraries like Intel MKL. Superficially at least, LoopVectorization is working at the top in order to improve what happens way down at the bottom. Is there any truth to the ideas that a) this is a deep source of the latency cost, having to manufacture careful Julia code that gets lowered through all the layers in just the right way; and b) you've demonstrated substantial opportunities for speed-up that would ideally be exploited much lower in the stack?

Yes, that is essentially it.

The LoopVectorization rewrite is as an LLVM pass, therefore occurring much lower in the stack. Aside from compilation benefits by occurring at the correct place, this also has the benefit of making supporting structs like dual or complex numbers, or arbitrary user-defined structs, a non-issue.