技术 / Java / ThreadLocal原理

[huanzhiyazi]

目录

• 1 预备知识——斐波拉契散列
• 2 ThreadLocal 核心结构
• 3 ThreadLocal 散列表读写
  • 3.1 散列表的清理
  • 3.2 散列表的冲突
  • 3.3 散列表的扩容

1 预备知识——斐波拉契散列[Top]

Java ThreadLocal 的作用是在当前线程维护一块线程独立（除了本线程外，其它线程无法访问到）的数据区来规避并发问题。其中为了实现对线程独立数据区的快速访问，ThreadLocal 将这块数据区保存在一个散列表中。我们暂且将该散列表叫做 ThreadLocal散列表。

ThreadLocal散列表采用 斐波拉契散列 方法实现散列函数。

具体而言，ThreadLocal散列方法用 黄金分割比魔数（0x61c88647） 作为散列乘数，以如下公式作为散列函数以实现最大程度减少冲突的目的：

hash(K) = (K * 0x61c88647) & (hashtable.len - 1)

其具体的散列原理可以参考 斐波拉契散列。

2 ThreadLocal 核心结构[Top]

上一节讲到，ThreadLocal 在当前线程维护了一个散列表，而这个散列表只能由当前线程自己访问，以此来避免该散列表内的数据并发问题。所以 ThreadLocal 基本的结构图如下：

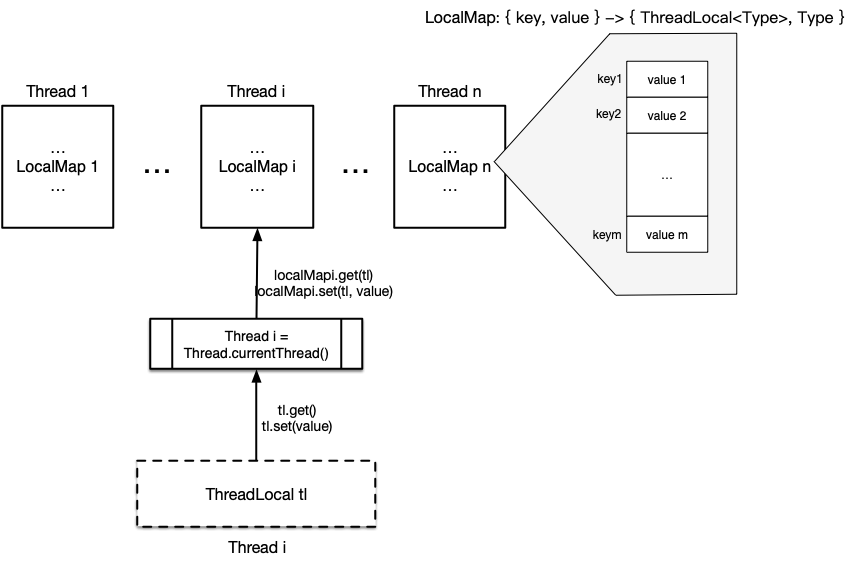
如图所示，关键点如下：

• 每一个 Java Thread 对象都保存一个散列表——LocalMap。实际定义如下：

public
class Thread implements Runnable {
    // ...省略

    /* ThreadLocal values pertaining to this thread. This map is maintained
     * by the ThreadLocal class. */
    ThreadLocal.ThreadLocalMap threadLocals = null; // 图中的 LocalMap

    // ...省略
}

LocalMap 的实际维护者为 ThreadLocal。

• 应用程序通过 ThreadLocal 确保只访问当前线程的 LocalMap。这包含两层意思：

  1. ThreadLocal 只访问当前线程的 LocalMap。这实际由 Thread.currentThread() 这个静态方法来保证。比如，在 ThreadLocal.get() 方法中，先通过 Thread.currentThread() 得到当前 Thread 对象，然后再读该对象中的 LocalMap 散列表：

  public T get() {
      Thread t = Thread.currentThread();
      ThreadLocalMap map = getMap(t);
  
      // ...从 map 中读并返回值
  }
  

  2. 如果不通过 ThreadLocal 也能引用到其它线程的 LocalMap。但是除非用反射，否则虽然有其它线程的 LocalMap 引用，但是却无法访问它。因为 LocalMap 中的所有方法都是私有的，只有外部类 ThreadLocal 有权限访问它们。

有了这个保证，如果有数据不希望被其它线程看到，就可以放心通过 ThreadLocal 存入 LocalMap 散列表。它的效果类似于一个局部变量（local parameter），都只对当前线程可见；只不过一般来说，其生命周期要长于局部变量，可访问范围也要大于局部变量。

• 每一个 ThreadLocal 对象都是散列表中的一个键（key）。键值从 1 开始递增，并通过以下散列函数映射到散列表中的索引位置：

hash(key) = (key * 黄金分割比魔数) & (散列表长度 -1)

3 ThreadLocal 散列表读写[Top]

LocalMap 是一个数组，根据斐波拉契散列原理，其长度必须是 2 的倍数。LocalMap 的读写需要解决三个关键问题：清理、冲突、扩容。

3.1 散列表的清理

LocalMap 中的元素是可被系统回收的，这样可以避免不再使用的对象长期滞留在散列表中占用内存空间。其散列表的定义如下：

static class ThreadLocalMap {

    // 散列表元素，是一个弱引用，本质是 ThreadLocal 是一个弱引用
    static class Entry extends WeakReference<ThreadLocal<?>> {
        /** The value associated with this ThreadLocal. */
        Object value;

        Entry(ThreadLocal<?> k, Object v) {
            super(k);
            value = v;
        }
    }

    // 散列数组
    private Entry[] table;

    // ...省略
}

可以想象这样一种情况，外部应用程序先生成了一个 ThreadLocal 对象，并保存在当前线程的散列表中。当外部应用程序不再用到该 ThreadLocal 对象时，将解除其引用（即设置成 null），其本意是要告诉 JVM，该对象可以被回收了。此时，如果 LocalMap 中仍然持有对该对象的强引用，则该对象虽然不再被使用，但是永远得不到回收的机会了，从而会导致内存泄露。所以散列表中对 ThreadLocal 的引用必须是 WeakReference 的，这样 JVM 才有机会释放它。

LocalMap 的清理过程是在读写 LocalMap 时进行的。

其中，LocalMap 的读清理示意图如下：

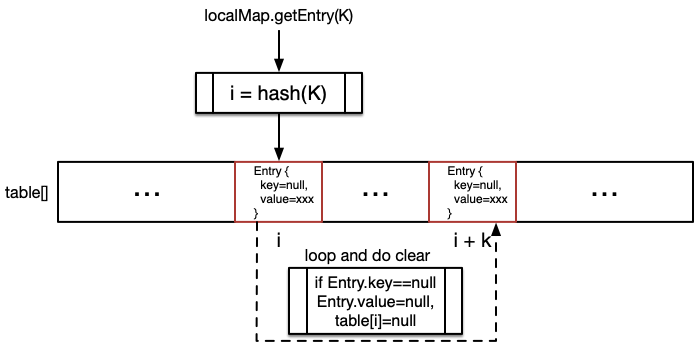
读步骤如下：

1. 以 ThreadLocal 作为 key（用 K 表示），用斐波拉契散列计算出在散列表（table）中的索引 i。
2. 若 table[i].key==null 说明存放在索引 i 处的 ThreadLocal 已经被系统回收，于是执行散列表读清理过程（步骤3）；否则找到，返回 table[i]。
3. 从索引 i+1 开始遍历整个散列表，若 table[i].key==null 则清理其 value 并将该位置置null；否则如果 hash(table[i].key)!=i，说明该元素是再散列过来的，将其重新散列到与 hash(table[i].key) 更近的位置。
4. 散列表读清理完成后，从 i 开始继续遍历散列表，如遇 table[i].key==K，说明要读的 ThreadLocal 是因为冲突通过再散列到该位置的，返回 table[i] 即可。
5. 没有找到符合要求的 ThreadLocal，返回 null。

值得注意的是，在散列表读清理步骤（步骤3）中，对不需要清理的元素又执行了一次再散列，目的是尽可能地将再散列过的元素重新散列到原来的位置，这样下次再读取该元素时，可以更快地命中。其关键代码如下：

private int expungeStaleEntry(int staleSlot) {
    Entry[] tab = table;
    int len = tab.length;

    // expunge entry at staleSlot
    tab[staleSlot].value = null;
    tab[staleSlot] = null;
    size--;

    // Rehash until we encounter null
    Entry e;
    int i;
    for (i = nextIndex(staleSlot, len);
         (e = tab[i]) != null;
         i = nextIndex(i, len)) {
        ThreadLocal<?> k = e.get();
        if (k == null) { 
            // 执行正常读清理过程
            e.value = null;
            tab[i] = null;
            size--;
        } else {
            // 执行再散列过程
            int h = k.threadLocalHashCode & (len - 1);
            if (h != i) { // 不在原来的位置，散列到与原位置更近的位置
                tab[i] = null;
                while (tab[h] != null)
                    h = nextIndex(h, len);
                tab[h] = e;
            }
        }
    }
    return i;
}

现在，看一下 LocalMap 的写清理过程：

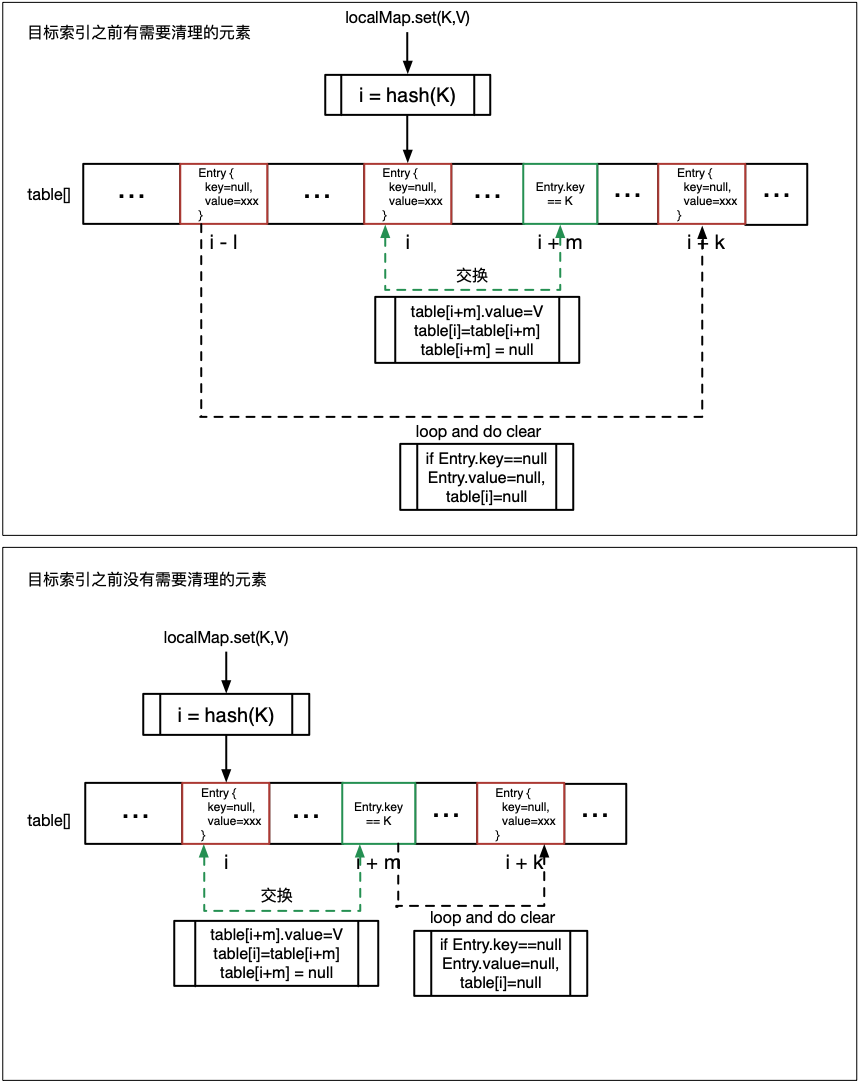
写步骤如下：

1. 以 ThreadLocal 作为 key（用 K 表示），用斐波拉契散列计算出在散列表（table）中的索引 i。
2. 若 table[i].key==null 说明存放在索引 i 处的 ThreadLocal 已经被系统回收，于是执行散列表写清理过程（步骤3）；否则若 table[i].key==K，执行写入 table[i].value=V 并返回。
3. 从索引 i+1 开始遍历整个散列表，若 table[i].key==K，则找到了再散列位置，执行写入并和原位置元素进行交换，这样写入的元素便散列到了原位置处，下次读写可以直接命中。
4. 交换后，如果原位置之前还有需要清理的元素，则从此处开始执行一次读清理过程，否则，则从再散列位置（交换后变为需要回收的元素）开始执行一次读清理过程。执行完读清理之后，再进行一次启发式读清理。
5. 若没有找到可交换的再散列位置，说明是一个新写入的值，直接生成一个新元素并保存到原位置，然后再执行一次启发式读清理。
6. 若步骤 2 的遍历中始终没有找到满足 table[i].key==null || table[i].key==K 的元素，说明遇到 冲突 了，在散列表下一个空位置中直接写入新值。
7. 最后执行一次启发式读清理，若没有任何元素需要清理且散列表有效元素个数达到阈值（>=散列表长度的2/3）则执行散列表 扩容。

可以看到，散列表的写入过程非常复杂，如果不关心太多细节，总的一个流程可以概括为：找到写入位置，若可写则写入；若不可写且需要清理，则找到再散列位置；若找到再散列位置，则写入并再散列回原位置，然后执行清理；若不可写且无需清理，则再散列到下一个空位置并写入（解决冲突）；最后进行启发式清理和尝试扩容。

所以，在写入过程中，同时需要解决清理、冲突和扩容三个问题。

步骤中多次遇到启发式清理，实际上是一个对数规模的循环读清理过程，代码如下：

private boolean cleanSomeSlots(int i, int n) {
    boolean removed = false;
    Entry[] tab = table;
    int len = tab.length;
    do { // 对数次循环
        i = nextIndex(i, len);
        Entry e = tab[i];
        if (e != null && e.get() == null) {
            n = len;
            removed = true;
            i = expungeStaleEntry(i); // 读清理
        }
    } while ( (n >>>= 1) != 0);
    return removed;
}

3.2 散列表的冲突

从 3.1 节的 LocalMap 写入过程可以看到，LocalMap 解决冲突的办法用的是开放定址法中的 线性探测再散列。在线性探测再散列中，如果遇到冲突，则按顺序往后寻找一个空闲位置进行插入。

那么为什么要用线性探测法呢？主要是因为简单和节省内存空间。虽然最坏情况下的时间复杂度需要 O(n)，但是考虑到 ThreadLocal 的使用场景只限制在少量元素的存储，所以时间复杂度并不是性能瓶颈。

接下来还有一个问题是，我们了解到 斐波拉契散列 是一种可以有效减少冲突的散列方法，甚至在多次测试中我们发现，LocalMap 散列表的散列效果是完美无冲突的（可能测试用例没有覆盖完全，期待证明过程）。所以，我们假定这个散列结果是完美的，似乎就不需要处理冲突了？其实不然，我们考虑一下下面这种情况：

• 对于散列规模为 2^4=16 来说，其散列结果如下：

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
7	14	5	12	3	10	1	8	15	6	13	4	11	2	9	0

• 现假定，在散列表中，中间大部分元素已经被回收或者删除，此时散列表内容如下：

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
7	×	×	×	3	×	1	×	×	×	×	×	×	×	9	0

此时，散列表的有效元素为 5，占总长度的 31%（5/16），没有达到扩容阈值（2/3），所以不会执行扩容操作。而下一个即将添加的 ThreadLocal 的 key 值为 17，执行散列函数 hash(17) = (17 * 0x61c88647) & (16 - 1) = 7，即散列位置为 table[7]。但是 table[7] 处的元素已经存放了 key 值为 1 的元素，于是产生冲突，根据线性探测法，将顺移到 table[8]。此时散列表如下：

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
7	×	×	×	3	×	1	×	×	×	×	×	×	×	9	0	8

3.3 散列表的扩容

散列表的扩容操作相对比较简单，关键步骤有 3 步：

1. 扫描一遍老散列表，清除无效元素。具体操作为每遇到一个需要清理的元素则执行一次读清理过程。
2. 申请一个两倍容量大小的新的空散列表。
3. 将老散列表中的元素重新散列到新散列表中。注意，重新散列时的散列函数要用新散列表的长度。

需要注意的是，扩容步骤 3 中的再散列过程也有可能发生冲突。当元素的 key 值超过新散列表的容量大小时，就有发生冲突的可能。

扩容代码如下：

private void rehash() {
    // 步骤 1：清理老散列表
    expungeStaleEntries();

    // 实际扩容阈值：(table.len * 2 / 3) * 3 / 4 = table.len / 2
    if (size >= threshold - threshold / 4)
        resize(); // 执行扩容
}

/**
 * Double the capacity of the table.
 */
private void resize() {
    // 步骤2：申请新散列表
    Entry[] oldTab = table;
    int oldLen = oldTab.length;
    int newLen = oldLen * 2;
    Entry[] newTab = new Entry[newLen]; 
    int count = 0;

    // 步骤3：将老散列表元素再散列到新散列表
    for (int j = 0; j < oldLen; ++j) {
        Entry e = oldTab[j];
        if (e != null) {
            ThreadLocal<?> k = e.get();
            if (k == null) {
                e.value = null; // Help the GC
            } else {
                int h = k.threadLocalHashCode & (newLen - 1);
                while (newTab[h] != null) // 扩容再散列也可能发生冲突
                    h = nextIndex(h, newLen);
                newTab[h] = e;
                count++;
            }
        }
    }

    setThreshold(newLen);
    size = count;
    table = newTab;
}

// O(n^2) 的清理
private void expungeStaleEntries() {
    Entry[] tab = table;
    int len = tab.length;
    for (int j = 0; j < len; j++) {
        Entry e = tab[j];
        if (e != null && e.get() == null)
            expungeStaleEntry(j);
    }
}

4 思考——为什么不直接散列到 key[Top]

我们注意到，ThreadLocal 作为 key 而言是递增的。稍微修改一下可以直接从 0 开始递增。那么直接按顺序存放到数组对应的索引位置不就可以了么？为什么要大费周章用一个斐波拉契散列来重新计算存放位置呢？

关于这一点我的理解是：

1. 直接散列到 key 的话，如果前面的元素被回收或者删除，就无法利用被删除的空闲位置。
2. 如果要利用空闲位置，一种办法是用 hash(key) = key % table.len 来计算。这实际上是一个除法散列。
3. 除法散列虽然可以避免内存空间的浪费，但是因为散列表的长度需要取素数，这就意味着除法散列不能转换为位移运算，只能直接求模，效率是很低的。

以上一些缺点，斐波拉契散列都可以避免，通过均匀的散列效果避免空间浪费，通过将乘法运算转换为位操作，提高了运算速度。