技术 / 算法 / 斐波拉契散列

[huanzhiyazi]

目录

• 1 乘法散列
• 2 斐波拉契散列
• 3 斐波拉契散列改造
• 4 原理初探
• 5 参考

1 乘法散列[Top]

斐波拉契散列是 乘法散列 的一种特例。乘法散列的散列函数表示如下：

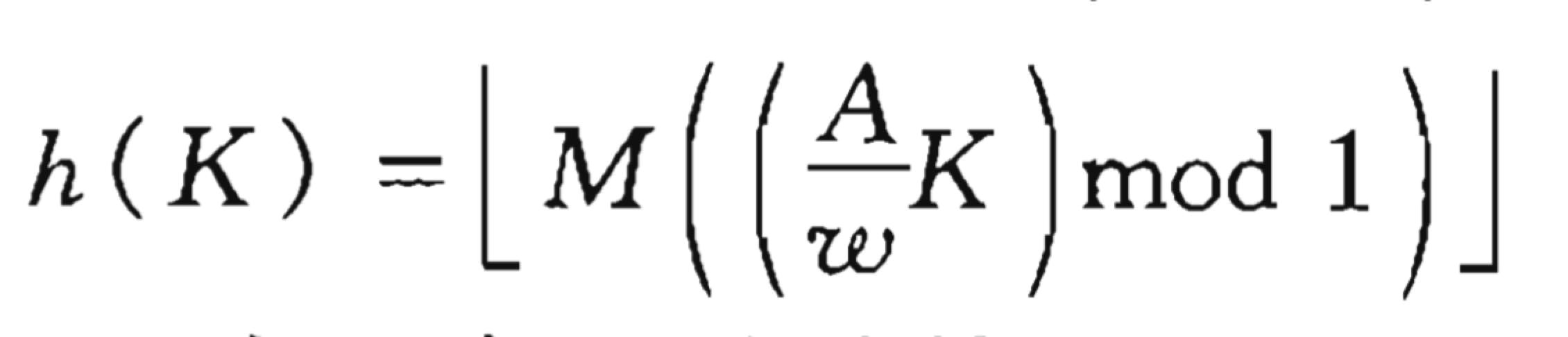
其中，K 是键值，M 是散列规模或散列范围，所以应有：0 ≤ h(K) < M，通常 M 在一台二进制计算机上是 2 的乘方。A 是一个常数，ω 是计算机字的大小，比如在 32 位机上 ω=2^32，A 与 ω 互素。mod 1 表示取小数部分的值。

假设 M=2^m，那么 h(K) 的计算过程就为：

1. 计算 a = A/ω；
2. 计算 a' = a×K；
3. 取 a' 的小数部分 d；
4. d 的二进制表示左移 m 位得到 h'；
5. 取 h' 的整数部分为 h，即：h = h' - ⌊h'⌋。

为了避免低效率计算浮点数，上述过程可以等价为如下步骤：

1. 计算 a = A×K；
2. 计算 a' = a % ω，即截取 a 的低位部分机器码长度，若 ω=2^32 则截取 a 的低 32 位为 a'；
3. 取 a' 的高 m 个二进制位作为 h，即 a' 右移 32-m 位得到。

2 斐波拉契散列[Top]

在实际应用中，一般取 A/ω 为 黄金分割比：A/ω = 1/φ = (sqrt(5) - 1) / 2 = 0.6180339887。所以在 32 位机器上，A = (sqrt(5) - 1) / 2 × 2^32 ≈ 2654435769。在这种情况下计算得到的散列值将均匀地分布在散列规模 M 内，即最大程度地减少发生冲突的可能性。我们称这样的散列方法为 斐波拉契散列。

之所以叫斐波拉契散列，是因为选定的黄金分割比 1/φ 与斐波拉契数列有着如下密切的关系：斐波拉契数列中前后两项数的比值无限接近于黄金分割比 1/φ。这点可以从斐波拉契数列的通项公式得到：

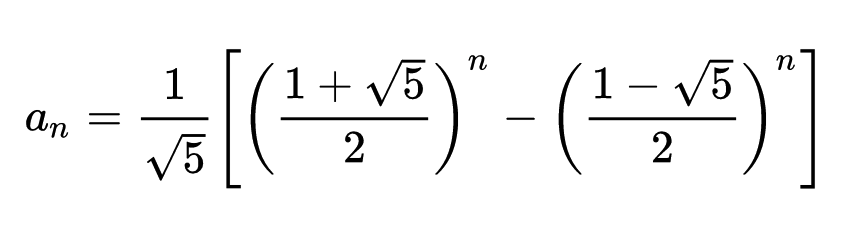
lim(f(n) / f(n+1)) = 2 / (1 + sqrt(5)) ≈ (sqrt(5) - 1) / 2 = 1/φ

可以直观感受如下。对于斐波拉契数列：1 1 2 3 5 8 13 21... 有：

f(1) / f(2) = 1 / 1 = 1
f(2) / f(3) = 1 / 2 = 0.5
f(3) / f(4) = 2 / 3 ≈ 0.666
f(4) / f(5) = 3 / 5 = 0.6
f(5) / f(6) = 5 / 8 = 0.625
f(6) / f(7) = 8 / 13 ≈ 0.615
f(7) / f(8) = 13 / 21 ≈ 0.619
...

作为例子，我们设：m=3,4,5; M=2^m，ω=2^32，则 A=0.6180339887×2^32=2654435769。

先按常规乘法散列方法计算：

void hashTest1(int m, long A, long w) {
    int M = (int)Math.pow(2, m);
    double theta = (double)A/w;
    String sq = "";
    for (int K = 1; K <= M; K++) {
        // compute h(K)
        double h = (theta * K - Math.floor(theta * K)) * M;
        sq += (int)Math.floor(h) + " ";
    }
    System.out.println(sq);
}

// 执行
hashTest1(3, 2654435769L, (long)Math.pow(2, 32));
hashTest1(4, 2654435769L, (long)Math.pow(2, 32));
hashTest1(5, 2654435769L, (long)Math.pow(2, 32));

执行结果为：

4 1 6 3 0 5 2 7 

9 3 13 7 1 11 5 15 8 2 12 6 0 10 4 14 

19 7 27 15 2 22 10 30 17 5 25 13 1 20 8 28 16 3 23 11 31 19 6 26 14 2 21 9 29 17 5 24 

按照移位等价方法计算如下：

void hashTest2(int m, long A, long w) {
    int M = (int)Math.pow(2, m);
    String sq = "";
    for (int K = 1; K <= M; K++) {
        // compute h(K)
        long h = ((A * K) % w) >>> (32 - m);
        sq += h + " ";
    }
    System.out.println(sq);
}

// 执行
hashTest2(3, 2654435769L, (long)Math.pow(2, 32));
hashTest2(4, 2654435769L, (long)Math.pow(2, 32));
hashTest2(5, 2654435769L, (long)Math.pow(2, 32));

执行结果为：

4 1 6 3 0 5 2 7 

9 3 13 7 1 11 5 15 8 2 12 6 0 10 4 14 

19 7 27 15 2 22 10 30 17 5 25 13 1 20 8 28 16 3 23 11 31 19 6 26 14 2 21 9 29 17 5 24 

两种方法得到的散列结果一样，且散列效果比较理想（只在 m=5 的时候出现了两次冲突）。

3 斐波拉契散列改造[Top]

还有一些其它的斐波拉契散列变种，目的是为了进一步减少冲突。比如将移位等价法稍作改造，在计算出 a' = A*K%w 之后，不取 a' 的高 m 位，而是取其低 m 位。这样还有一个好处，即只需计算 a' = A*K，不用再进行求模运算了，因为求模本质上就是取低位部分的二进制位，所以不管求不求模，最终取到的低位部分都是一样的。

仍然以上一节的例子来进行验证：

void hashTest3(int m, long A) {
    int M = (int)Math.pow(2, m);
    String sq = "";
    for (int K = 1; K <= M; K++) {
        // compute h(K)，取低 m 位
        long h = (A * K) & (M - 1);
        sq += h + " ";
    }
    System.out.println(sq);
}

// 执行
hashTest3(3, 2654435769L);
hashTest3(4, 2654435769L);
hashTest3(5, 2654435769L);
hashTest3(6, 2654435769L);

执行结果为：

1 2 3 4 5 6 7 0 

9 2 11 4 13 6 15 8 1 10 3 12 5 14 7 0 

25 18 11 4 29 22 15 8 1 26 19 12 5 30 23 16 9 2 27 20 13 6 31 24 17 10 3 28 21 14 7 0 

57 50 43 36 29 22 15 8 1 58 51 44 37 30 23 16 9 2 59 52 45 38 31 24 17 10 3 60 53 46 39 32 25 18 11 4 61 54 47 40 33 26 19 12 5 62 55 48 41 34 27 20 13 6 63 56 49 42 35 28 21 14 7 0 

可以看到，在 m=3,4,5,6 时，散列结果都没有产生冲突（但并不代表在所有情况下都没有冲突）

同时，注意 2654435769L 的二进制表示为：

...省略高32位0... 1 0 0 1 1 1 1 0 0 0 1 1 0 1 1 1 0 1 1 1 1 0 0 1 1 0 1 1 1 0 0 1

关注低 32 位，在 java 中若用 int 来表示该二进制，则最高位为 1 是一个负数，该二进制序列实际上是补码表示，那么其原码表示应为：

1 1 1 0 0 0 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 1 1 1

即十进制的 -1640531527 （也即 (int)2654435769L 进行强制转换后的溢出结果）。

而实际上我们也可以用 -1640531527 来代替 2654435769L 达到同样的目的。

进一步，在上述散列方法中，进行乘法和移位运算过程中始终不必关心符号位，所以以下两个二进制序列对散列结果的计算没有影响：

-1640531527
1 1 1 0 0 0 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 1 1 1

1640531527 (0x61c88647)
0 1 1 0 0 0 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 1 1 1

注意到，在 java ThreadLocal散列表中，其散列方法中用到的魔数 A 就是 0x61c88647。

其散列计算如下：

void hashTest4(int m, int A) { // 魔数 A 为 int 型
    int M = (int)Math.pow(2, m);
    String sq = "";
    for (int K = 1; K <= M; K++) {
        // compute h(K)
        int h = (A * K) & (M - 1);
        sq += h + " ";
    }
    System.out.println(sq);
}

// 执行
hashTest4(3, 0x61c88647); // 或 hashTest4(3, -1640531527);
hashTest4(4, 0x61c88647); // 或 hashTest4(4, -1640531527);
hashTest4(5, 0x61c88647); // 或 hashTest4(5, -1640531527);
hashTest4(6, 0x61c88647); // 或 hashTest4(6, -1640531527);

执行结果为：

7 6 5 4 3 2 1 0 

7 14 5 12 3 10 1 8 15 6 13 4 11 2 9 0 

7 14 21 28 3 10 17 24 31 6 13 20 27 2 9 16 23 30 5 12 19 26 1 8 15 22 29 4 11 18 25 0 

7 14 21 28 35 42 49 56 63 6 13 20 27 34 41 48 55 62 5 12 19 26 33 40 47 54 61 4 11 18 25 32 39 46 53 60 3 10 17 24 31 38 45 52 59 2 9 16 23 30 37 44 51 58 1 8 15 22 29 36 43 50 57 0 

4 原理初探[Top]

在 Knuth 的分析中，给出了一个有趣的事实，对于黄金分割比 1/φ 来说，设 {x} 表示 x 的小数部分。那么在线段 [0...1] 中，逐次标注点 {1/φ}, {2×1/φ}, {3×1/φ},...，则每个新增加的点都会落入最大剩余区间之一，且按照黄金分割比来分割这个最大剩余区间。如下图所示：

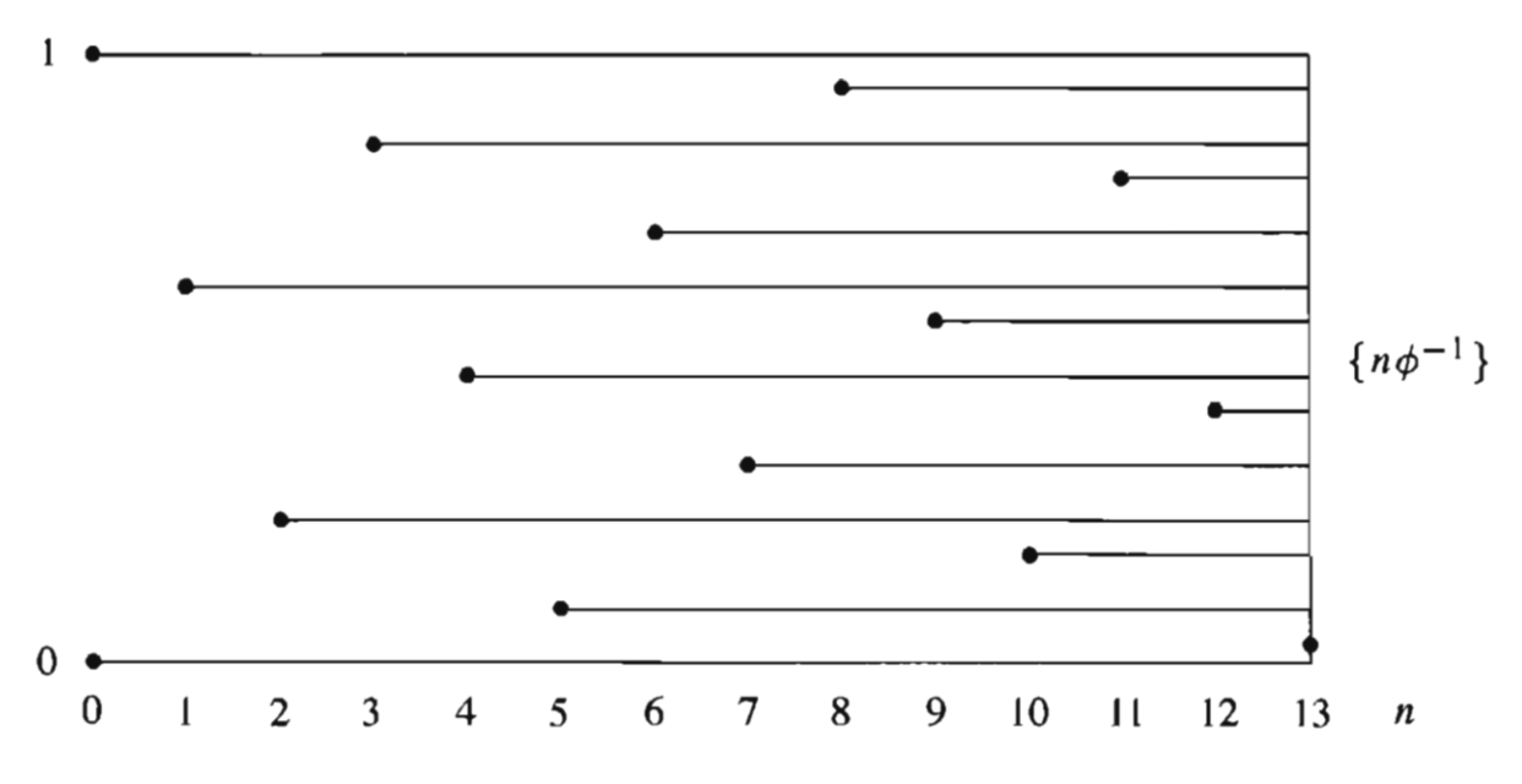
此外，我们还注意到，如果分别计算出 [1,2,...]×魔数A，且并列列出这些结果的低 32 位二进制序列，就能发现，除了取低位作为散列结果以外，取其它位置的的部分二进制位作为散列结果，也能得到较好的散列效果：

图中框出了较好散列效果的列。

实际上，一个较好的经验是，将机器字长能表示的最大整数乘以黄金分割比得到一个魔数 A，然后按照乘法散列的方法来计算出散列结果。因为我们可以看到，魔数 A 的连续倍数在很多指定的二进制序列范围内分布是比较均匀的，这样做的结果是可以尽可能的减少冲突发送的概率。

5 参考[Top]

Knuth 计算机程序设计艺术第 6.4 节散列