Fix diagram symbols for phase inversion and complement.

[dariosanfilippo]

Hello, people.

Just a small thing that I mentioned in the past and that I'm putting here not to forget about it: Faust's diagrams represents multiplication by -1 (try process = *(-1);) with the following symbol:

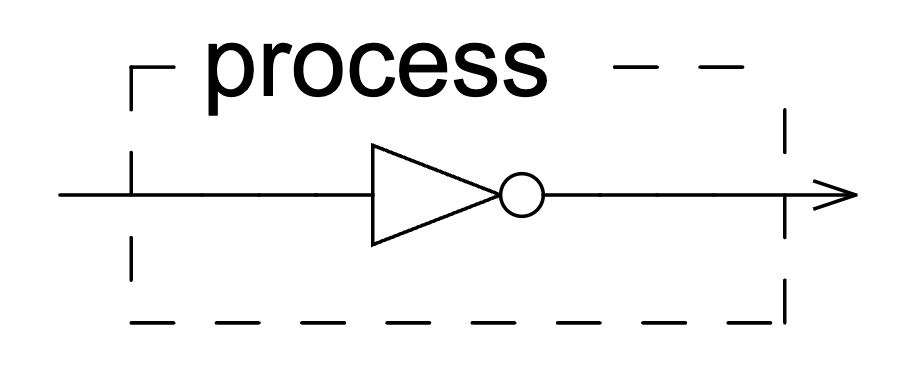
which usually represents negation. We could perhaps use the symbol above for (x).(1 - x) signals when x is in [0..1]. The common "crossed O" representing phase inversion would be best for multiplication by minus one.

Best, Dario

[tomoyanonymous]

"Crossed O”-solution looks nice for me too. Using a special symbol for phase inversion is indeed useful(e.g. it makes it easier to read the diagram of zita_rev) but I was a bit confused when constructing complex binary logic on faust.

But applying existing triangle symbol to (x).(1 - x)(where x:0..1) will need some discussions.

• Should we allow non-integer 1.0 or not?

According to the source, at least 6 cases should be captured to express just *(-1).

-1  ,  _   : *
_   ,  -1  : *
-1.0,  _   : *
_   , -1.0 : *
0   ,  _   : - 
0.0 ,  _   : -

https://github.com/grame-cncm/faust/blob/fd39eb6375914db8746d9fa9c0410c6e3601abff/compiler/global.cpp#L632-L638

In the normalized form, the numeric values are statically typed to interger and float.

gNagation[0] = boxSeq(boxPar(boxInt(1), boxWire()), boxPrim2(sigSub));
gNagation[1] = boxSeq(boxPar(boxReal(1.0), boxWire()), boxPrim2(sigSub));//should we allow this?

For me, using 1.0-x is likely to be happen other than the case of logical negation so we should not though user have to explicitly cast using int if they wants to represent binary logic.For me, use of 1.0-x is likely to happen in the other the case than the logical negation too so we should not (though then user have to cast using int operator explicitly if they wants to represent binary logic).

• How should we ensure the range of input within 0 to 1?

Because faust does not have an internal boolean type, we can not ensure the input range is within 0 to 1. Thus the symbol in the diagram may represent wrong behaviour if the input range is not correct, different from the case of phase inversion.

Also, the case like x.(x * -1)+1 or x.(-x+1) which I prefer to represent binary negation will not be captured correctly with the x. 1-x pattern. Maybe new standard library function should be introduced. (BTW, the word choice is also difficult. ma.neg means *-1 and ma.inv means 1/x in the standard library...)