Add graph_grad function

[IlyaOrson]

In the Deep Implicit Layers tutorial from NeurIPS 2020, a very nice grad_graph function was used to make things clearer, around minute 23.

Is that function available elsewhere? If not, could it be added to the library?

I think it would be generally useful as a way to explore how things work in Jax.

[mattjj]

Thanks for this suggestion! It certainly seems worth considering.

Here's the version I used in the demo. It'll probably bit-rot unless we merge it into JAX.

I agree it seems like a useful tool for user exploration as well as for presentations, and it is pretty lightweight. I'm interested to hear other opinions though!

[kratsg]

Longer twitter thread here: https://twitter.com/lukasheinrich_/status/1340042422223572993 and was asked to add in a (not-so-naive apparently) suggestion: https://twitter.com/SingularMattrix/status/1340306739191672832

It would be nice to have a way to label in jax (both input arrays as well as computational calls) so I can annotate such a graph. I guess an expected API might be like

x = jnp.array(..., label="observations")
y = jnp.sum(x, axis=0, label='calculate sum(logpdf)')

or similar.

[niklasschmitz]

Good to see the issue already opened :+1: Here's also the variation from said twitter thread, reusing @mattjj's gist to graph any jaxpr: jaxpr_graph.py

[niklasschmitz]

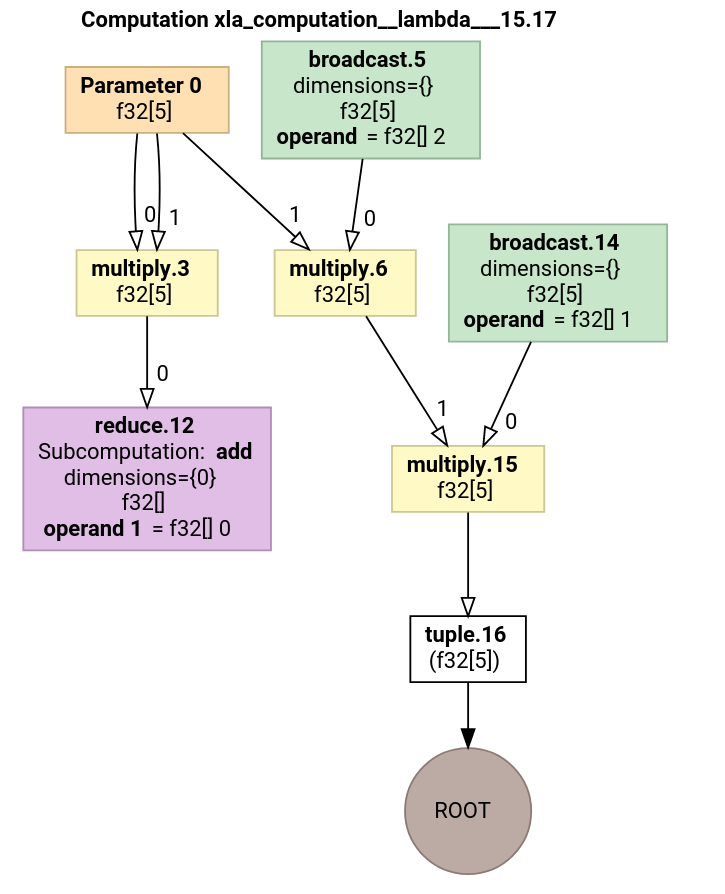
Just found that jaxlib.xla_extension.XlaComputation.as_hlo_dot_graph exists and can be used for similar results:

import jax
import graphviz

def hlo_graph(f, *args, **kwargs):
    comp = jax.xla_computation(f)(*args, **kwargs)
    graph = graphviz.Source(comp.as_hlo_dot_graph())
    return graph

which gives

import jax.numpy as jnp
f = lambda x: jnp.sum(x**2)
x = jnp.ones(5)
hlo_graph(jax.grad(f), x)

[mattjj]

Indeed! Some brainstorming on the differences:

• grad_graph can handle data-dependent Python control flow, unlike xla_computation (actually, this was the main desideratum for that demo in the implicit layers tutorial, since the fwd iteration implementation had a Python while loop in it!)
• the jaxpr IR has some differences with the XLA HLO IR, e.g. it shows custom derivative rules and some primitives like scan, so it's a slightly higher-level representation in some respects (while the HLO representation has the advantage of being more explicit about actually gets executed, especially the optimized HLO)
• the colors, labels, etc are more hackable in the pure-Python version
• the XLA HLO tools are much more developed than the quick hack in the gist

[niklasschmitz]

Cool! Also, I see now that my jaxpr_graph example, where using jax.make_jaxpr, fails on data-dependent Python control flow, while grad_graph works fine with extracting the jaxpr directly from the vjp. Is there a better/similar-to-vjp way to get a traced jaxpr for this purpose?

Regarding labelled subcomputations, would this call for a dedicated Tracer already?

I certainly appreciate the hackability aspect! Learning a lot about jaxprs here.

[pharringtonp19]

Is the code used to produce memory_ratio available? That looks helpful too.

[danielsnider]

+1 I'm looking for the memory_ratio code from this timestamp in the video.

I cannot find this in the NeurIPS colabs.

[raj-brown]

Hi @mattjj , do you have the for memory_ratio as well, and can you please share that? Thanks!

[mattjj]

Oops, sorry, I only just saw these requests for memory_ratio. (I came back to this thread because I wanted to make a new version of grad_graph for an upcoming talk.)

I did a search to find my colab notebook from the talk. Unfortunately this code may have bitrotted. I'll just paste what was in that notebook, and then maybe I can try to fix it at some point.

def memory_ratio(fun, *args):
  return _rev_mode_memory(fun, *args) / _fwd_eval_memory(fun, *args)

def _rev_mode_memory(fun, *args):
  _, fun_vjp = jax.vjp(fun, *args)
  res_memory = sum(x.nbytes for x in fun_vjp.args[0].args[0])
  jaxpr = fun_vjp.args[0].func.args[1]
  lit_memory = sum(np.array(l).nbytes for l in _jaxpr_literals(jaxpr))
  return res_memory + lit_memory

def _jaxpr_literals(jaxpr):
  for eqn in jaxpr.eqns:
    for v in eqn.invars:
      if type(v) is core.Literal:
        yield v.val
  for subjaxpr in core.subjaxprs(jaxpr):
    yield from _jaxpr_literals(subjaxpr)

# To track active sets properly, preserve python program order by
# monkey-patching in a sequence id. To do this right we'd make a new transform.
count = itertools.count()
def _new_eqn_recipe(invars, outvars, primitive, params, source_info):
  return pe.JaxprEqnRecipe(object(), invars, map(ref, outvars), primitive,
                           params, next(count))

def _fwd_eval_memory(fun, *args, **kwargs):
  args_flat, in_tree = tree_flatten((args, kwargs))
  flat_fun, out_tree = flatten_fun(lu.wrap_init(fun), in_tree)
  return _fwd_eval_memory_(flat_fun, args_flat)

def _fwd_eval_memory_(fun, args):
  in_pvals = [pe.PartialVal.unknown(core.get_aval(x)) for x in args]
  pe_new_eqn_recipe, pe.new_eqn_recipe = pe.new_eqn_recipe, _new_eqn_recipe
  try:
    jaxpr, _, _ = pe.trace_to_jaxpr(fun, in_pvals)
  finally:
    pe.new_eqn_recipe = pe_new_eqn_recipe
  eqns = sorted(jaxpr.eqns, key=op.attrgetter('source_info'))

  available_vars = set() # set(jaxpr.invars)  # don't count input storage?
  availables = []
  for eqn in eqns:
    availables.append(available_vars)
    available_vars = available_vars | set(eqn.outvars)

  used_downstream = set(jaxpr.outvars)
  actives = []
  for eqn, available in reversed(zip(eqns, availables)):
    used_downstream |= set(v for v in eqn.invars if isinstance(v, core.Var))
    actives.append(used_downstream & available)
  actives.reverse()

  size = lambda v: v.aval.nbytes.fget(v.aval) if hasattr(v.aval, 'nbytes') else 0
  return max(sum(size(v) for v in vs) +
             sum(np.array(l.val).nbytes for l in eqn.invars
                 if isinstance(l, core.Literal))
             for vs, eqn in zip(actives, eqns))

[raj-brown]

Thank @mattjj for pasting it here. I just had a question what module is pe in pe.JaxprEqnRecipe? Thanks!

[mattjj]

Ah sorry, bad form not to include the imports. I think they're the same as in this gist I linked in the comment above, modulo the _src module which we added later. In particular pe is usually jax._src.interpreters.partial_eval.