acb_poly functions request

[arbguest]

Would it make sense to add functions like conj, real_part, imag_part, and abs for acb_poly? My use case is that I have an acb->acb function and I am using acb_poly to find its complex derivative automatically, and the function uses conj, real_part, imag_part, and abs.

[fredrik-johansson]

I assume that conj, real_part, imag_part apply per-coefficient. How is abs defined?

[arbguest]

My reasoning was that if Re and Im are defined then you could do abs as sqrt(Re^2 + Im^2) using the 'series' variants of sqrt, squaring, and addition but I haven't thought too deeply about it.

[fredrik-johansson]

Yes, that is reasonable. So it should actually be an abs_series method.

[rudolph-git-acc]

Appreciate this is an older question, but I have also hit the lack of conj, abs, max, imag & real part functions when using arb_poly and acb_poly. The work-around below (for abs, but easily adjustable for the other functions) worked fine for me.

//procedure to calculate the absolute value of an acb_poly function
void
acb_poly_abs_series(arb_poly_t res, const acb_poly_t p, slong prec)
{
    acb_t a, one; 
    acb_init(a);
    acb_init(one);

    arb_t abs;
    arb_init(abs);
 
    acb_set_si(one, 1);
    acb_poly_evaluate(a, p, one, prec);
    acb_abs(abs, a, prec);

    arb_poly_set_arb(res, abs);
 
    arb_clear(abs);
    acb_clear(a);
    acb_clear(one);
}

[fredrik-johansson]

I don't understand what that code is meant to do. Absolute value of the sum of the coefficients, how is that useful?

[rudolph-git-acc]

@fredrik-johansson

It probably not so much 'useful', but could be 'practical' once everything else is in acb-poly. Suppose we have to code a complex valued function like this one:

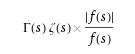
where f(s) is a complex polynomial. The Gamma and Zeta functions could be coded in ARB using acb or acb_poly functions. Once you pick the latter, it is just convenient to have all functions and variables as acb_poly hence an acb_poly_abs_series function keeps the code more readable (the actual example where we encountered this problem is much more complicated and involves many different sub-functions).

P.S.: Just to let you know that we have been quite heavily (and successfully) using ARB to find numerical evidence for this polymath project: https://terrytao.wordpress.com/2018/01/24/polymath-proposal-upper-bounding-the-de-bruijn-newman-constant/

Very impressed by the robustness of your software as well as by the tremendous speed gains that it has brought us (up till a factor 20-30 faster than pari/gp). So far we haven't encountered a single bug in the software. Well done!

Only found two minor typo's in the documentation:

(y=z or z=y)

(slong src should be acb_t src in the first line)

Two questions about possible limitations/missing functions have come up that I will raise as a separate issue to keep this thread clean.

[fredrik-johansson]

I understand the application but the acb_poly_abs_series function you provided makes no sense to me.

[fredrik-johansson]

Thanks for the info about the polymath project and for the typos!

[rudolph-git-acc]

To convert a value in acb_poly back to an acb_t-varibale, I evaluate the polynomial for a value p at x=1 (i.e. assuming the coefficients encode the value p) and thereby obtain a complex value stored in an acb_t variable. Any acb_t function like abs, conj, etc. can then be applied to it and the result value is then 'encoded' in a new polynomial (of type arb_poly and acb_poly respectively).

I attach a simple test-script to show that this actually works well for abs and conj using an input value z = x+yi. I definitely don't rule out that my logic is wrong and some other mechanism gives the correct result 'by coincidence', but keen to understand what is going on!

TestcodeAbsCon.txt

[fredrik-johansson]

Your test code only uses length 1 polynomials. What does it mean for the coefficients to "encode the value" when the length is > 1?

[rudolph-git-acc]

Ah. You are correct. I am indeed using length 1 polynomials and that's why it works. The concept of abs for polynomials with length > 1 doesn't make much sense, since one would first need to evaluate the polynomial for a chosen x (not necessarily 1) to obtain a value to then apply the abs to.