Fix integer float number=
Inspired by this article:
https://blog.codingconfessions.com/p/how-python-compares-floats-and-ints
And this embed:
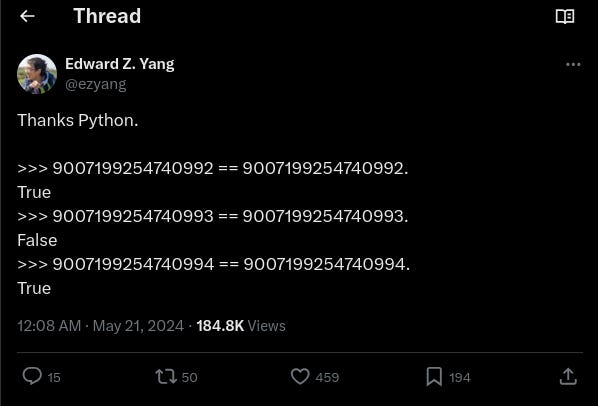
I thought I'd see how we handle it, and I think we have a different bug:
IN: scratchpad 9007199254740992 9007199254740992. number= .
t
IN: scratchpad 9007199254740993 9007199254740993. number= .
t
IN: scratchpad 9007199254740994 9007199254740994. number= .
t
What would be the bug ? I mean there will always be counter-intuitive results with floats, so it's best to be explicit for everything ?
With the current results that you showed, one big problem is that number= is not transitive: A=B and B=C but A!=C
9007199254740992 9007199254740993. number= .
t
9007199254740993. 9007199254740993 number= .
t
9007199254740992 9007199254740993 number= .
f
It all depends on what we want number= to mean for a float and something that is not float: "the closest representing float is the given float" vs "this is exactly represented as the given float". We have the former and it breaks transitivity. The latter would allow transitivity but would make number= pretty useless for everything that is not exactly represented as a float (always return false).
Maybe transitivity is too important and surprising to lose for a word named "equal", and both behavior should have separate names ?
Another approach in this specific case is to check the float has no fraction (ends in .0) and convert the float to an integer and compare. That would take some larger change since this is MATH: dispatch…
But, that would return true in all 3 cases.
I’m not suggesting anything, and don’t want to rush to change anything… but perhaps we can improve something.
I concur with @jonenst first statement. The original "bug" in the Python code is that 9007199254740993. is not representable as double, leading to wrong assumptions about the second comparison.
Another simple show-case is:
0.3 0.3 + 0.6 number=
t
0.3 0.3 0.3 + + 0.9 number=
f
0.3 0.3 0.3 0.3 + + + 1.2 number=
t
As you see, the "error" even corrects itself.
Should the compiler have thrown a warning? I don't think that these warnings are useful. It was a) clearly a constructed case to show a point and b) could only be done reliably for literals and would miss most of the real problematic cases.
I am not entirely sure but I think you cannot maintain transitivity and implicit conversion from decimal to binary. My main argument revolves around the idea that the "window" between two decimal representations has a different size than the "window" between two binary representations. So, the windows do not align with each other. You will always find three values that fall into two neighboring windows in each representation but where the "middle" value will fall into the smaller window in one representation and the large in the other. This will break your transitivity.
All this being said: I personally favor (and tell so my students) that comparison with floats must always be accompanied by a meaningful error margin (usually called the ε environment). So, while being a bit of a pain, I would argue for a float= ( a b ε -- * ) function that takes 3 arguments. From my perspective it is always a programmer error to compare two floats and not specify an ε, because it means you have not understood the intricacies of working with floats and should not be using them.
The second advice I give my students is that they should use inequality comparison operators like > and < whenever possible. This avoids many problems with floats from the start while putting away with the ε environment. (Actually, you integrate your expectation for ε into the bound, but that is another topic.) So, to foster this, one could simply refuse to compare floats with the usual comparison operators and force programmers to use inequalities or a comparison with explicit ε.
Another simple fact is loss of monotonicity of arithmetic functions like +.
IN: scratchpad 0.0000000000000000000000000000000000001 [ 0.0 number= . ] [ 1.0 + 1.0 number= . ] bi
f
t
So, while 1e-37 is clearly not equal to zero. Adding 1.0 makes it equal to 1.0 because of rounding loss. Should the runtime have thrown an error? Well, the computer world up to now agreed not to. Again, it is considered a programmer error not to have perceived the incompatibility of 1e-37 and 1.0 regarding addition. These are things you must know about your input data or you will have bugs. Floats are almost always the wrong datatype for comparisons. In my opinion the best a programming language can do is make it inconvenient for floats to be used in that way in the first place. E.g. by having good documentation, offering good alternatives (arbitrary precision numbers) and not offering misleading functionality like number= on floats that doesn't (at the very least) warn you about your misuse.
True, and we have ~ for that kind of comparison.
I think the intention of the number= is something kind of like eq? but allowing coercing.
Of course (how could I not have checked before typing... ;) )! Then, number= clearly should print a warning, because exact comparison of coerced floats is more often wrong than right. I could even think of not offering coercion to float in number= and to surmount that with documentation on better practices.
Specifically related to integer coercion, we could maybe assert that's its below 2^53+1.
https://stackoverflow.com/a/3793950/8031
Then if they for sure want it to do the old behavior, they could coerce before calling number=.
For other coercion, like ratios to floats, I'd have to think about other ideas.
Of course, disallowing it in the case of floats might be a good idea but also i kinda like stuff working that can work.
ERROR: not-representable-as-float n ;
: assert-representable-as-float ( n -- n )
dup 64-bit? 53 24 ? 2^ [ neg ] keep between?
[ not-representable-as-float ] unless ; inline
well if you are going to support integers that are perfectly representable as a float, probably you should support the subset of bignums (9007199254740992, 9007199254740994, 9007199254740996 ... and then +4 +4 +4 and then +8 +8 +8 ..etc) and the ratios (1/2 but not 1/3 or 1/10)
Would it, at that point, not be easier to just convert the number to float and back and see whether it is eq? to the original?
Probably and a stderr warning issued? If they need that coerced behavior they could pre-convert to floats before comparison in that part of the code?