1day_1paper
 1day_1paper copied to clipboard
1day_1paper copied to clipboard
[98] ASAM: Adaptive Sharpness-Aware Minimization for Scale-Invariant Learning of Deep Neural Networks
역시 이런 류는 icml 이지.. 대부분의 sharpness 연구들은 scale dependency problem 이 있다. #126 요 문제를 해결하는 metric 들이 제안되었는데, (1, 2, 3, 4) metric들을 제안한 paper들이 직접 학습들을 돌려보고 하지는 않았다.
3개의 contribution.
- Adaptive Sharpness 제안
- stronger correlation with generalization than sharpness does
- adaptive sharpness를 활용한 learning 방법 제안
- weight scale 에 따라 region을 maximization 하는 쪽으로 학습을 시킴
- 실험적으로 증명
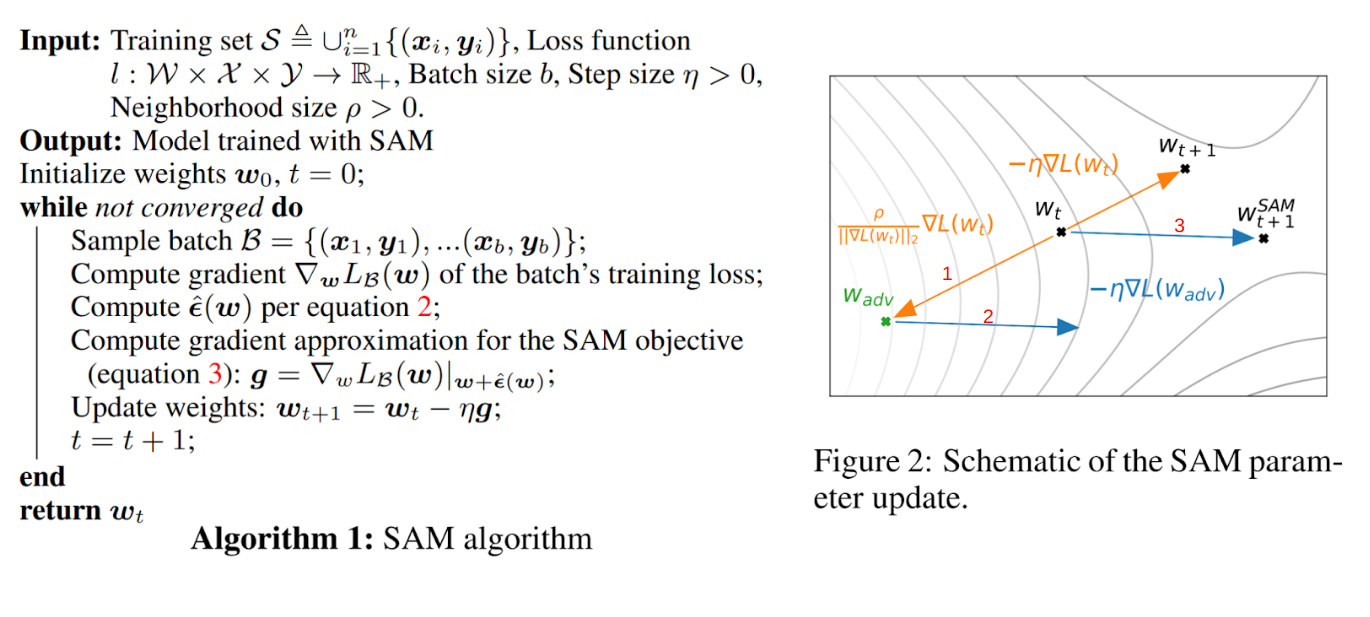
SAM
SAM(#127) 설명은 생략.
SAM 결론만 살펴보면 다음과 같다.
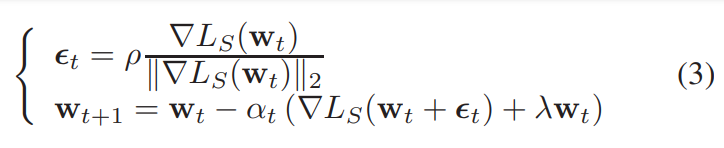
ASAM
A가 loss function을 바꾸지 않는 scaling operator라고 할 때, (#126 참고)
분명 loss contour 등고선 간의 region 이 좁아질 수 있는데, 이럴 때도, $\rho$ 값이 유지되는건 문제가 있다.
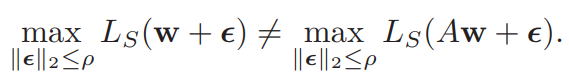
우선 Normalization operator 를 정의한다. ${\huge T_w, w \in \mathbb{R}^k}$ 가 invertible linear operator 들이라고 놓자. given weight $w$ 에 대해 loss function을 건들이지 않고 ${\huge T^{-1}_{Aw}A = T^{-1}_w}$ 이라면 ${\huge T^{-1}_w}$ 를 normalization operator 라고 하자.
이를 만족시키는 $T_w$ 는 다음 두개를 써 볼 수 있다.

실제로 $T_w$ 를 계산할 때는, 안정성을 위해 $T_w +ηI_k$ 형태로 작은 $η$ 를 함께 썼다. (0.05) https://github.com/SamsungLabs/ASAM/blob/f156a680171db16d551c0d85cba2514fa3bff6a2/asam.py#L24
Adaptive sharpness 는 다음과 같다.
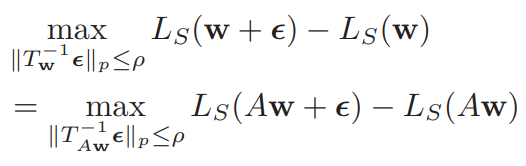 논문에서 증명한 properties 까지 담고 있는 식.
결국, sharpness 값이 transformation 과 무관하게, 일정하게 나오게 만들어 준다는 것이다.
논문에서 증명한 properties 까지 담고 있는 식.
결국, sharpness 값이 transformation 과 무관하게, 일정하게 나오게 만들어 준다는 것이다.
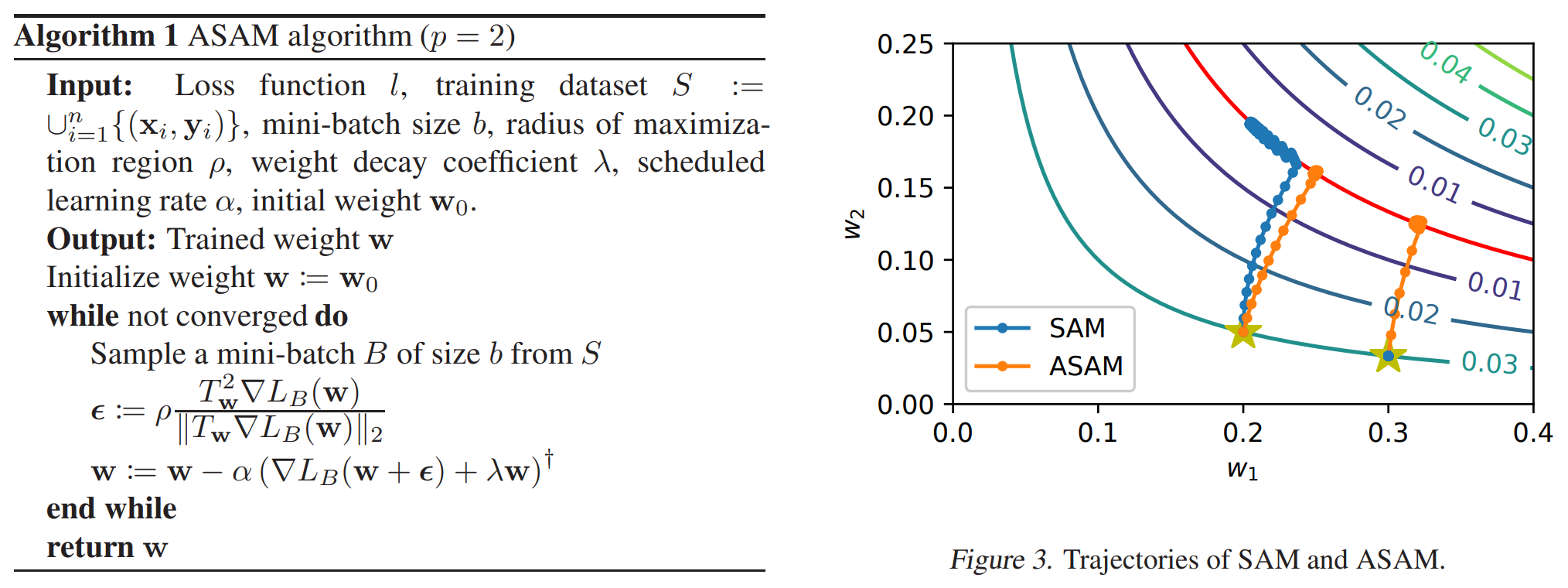
$w = (1, 1)$ 에 scaling operator $A=diag(3, 1/3)$ 을 곱해서 $w^{'} = (3, 1/3)$ 가 나왔다 가정하자.
파란색 line 위의 w 기준으로 SAM 에서처럼 $\max{L(w+\epsilon)}$에 해당하는 $\epsilon$ 값을 구해서 weight 를 구하고, Transforms들을 적용하면서, 빨간 line 을 그린다.

제안하는 방법은 epsilon ball 에도 transform 이 적용이 된다. (그림 참고)
generalization gap 은 mini-batch size, initial learning rate, weight decay coefficient, dropout rate 4개를 변경해 보면서, generalization gap 을 측정했다.
정의한 adaptive sharpness 와 correleation 을 찍어보면 유의미하다.
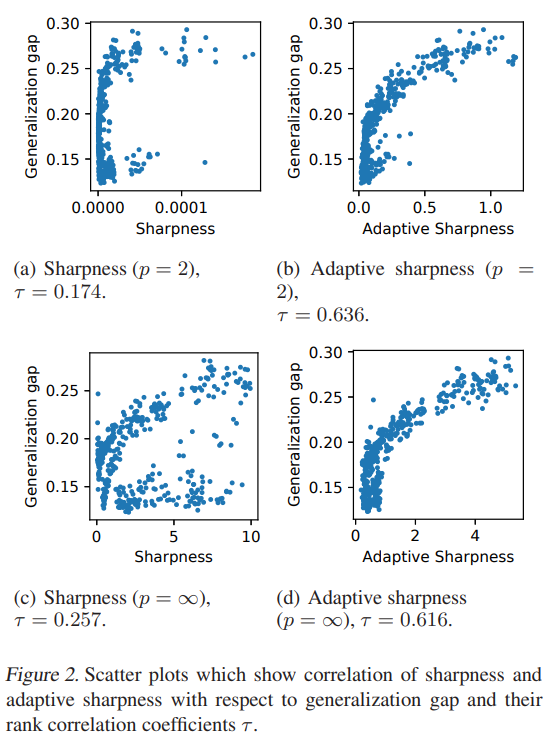
Adaptive Sharpness-Aware Minimization
그래서 minimization 은 어떻게 하냐.
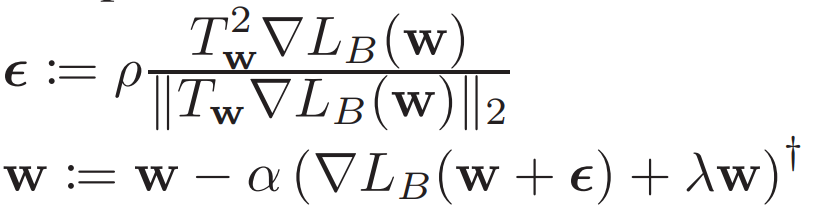
Results
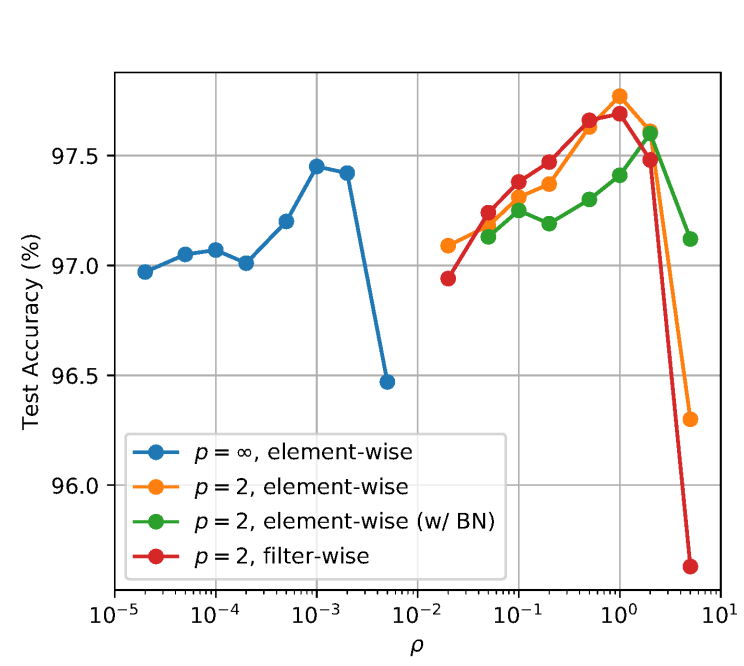
norm 은 L2 쓰는게 좋다. $\rho$ 값은 여전히 hyperparameter.
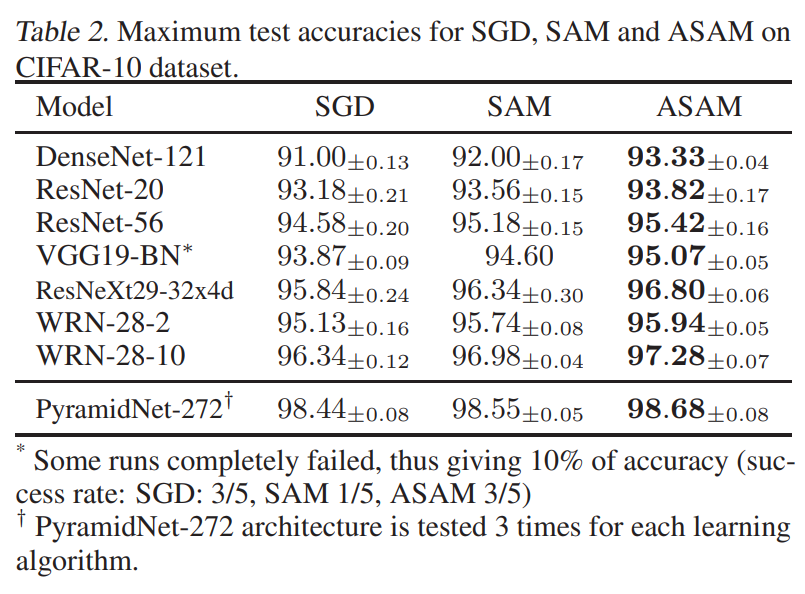
cifar-10
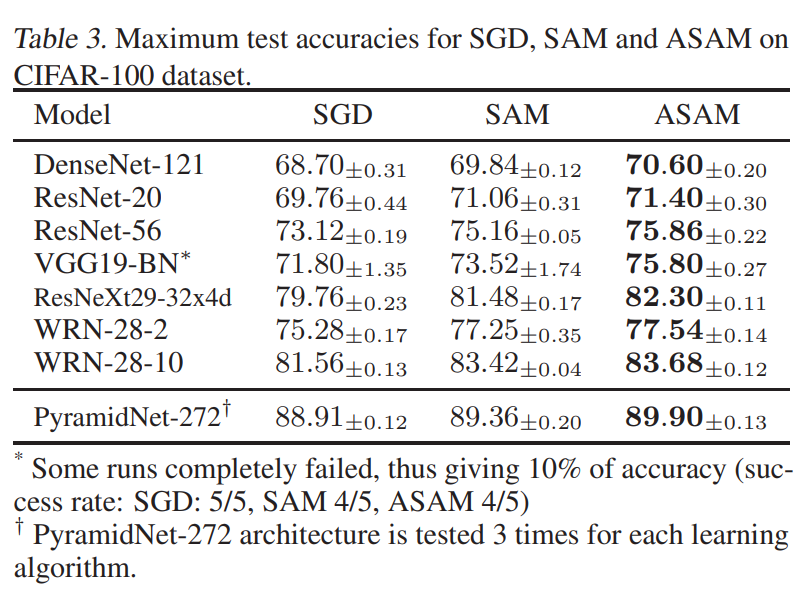
cifar-100
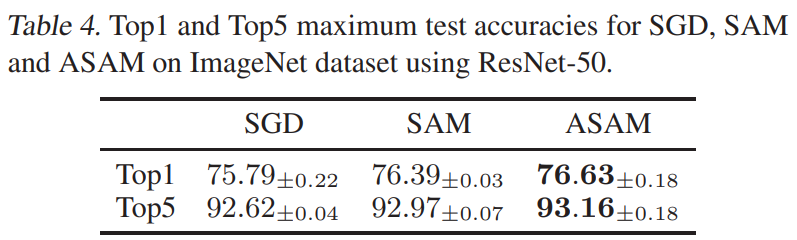
Imagenet
MNT (DE-EN)
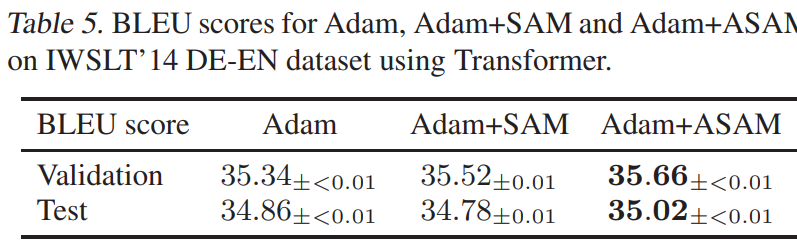
SAM 은 라벨 노이즈에 강인하다?