Conservation of flux function failed

[jillelee]

When running the dam-break(shallow_1d) example, I found the flux function not conversed very well.

I tried both Fortran and Python as kernel language, the error are the same and it is as high as 10^{-8}. Btw, I compared the outputs from Fortran and Python and the results are also the same. It seems that there’s something higher up in the PyClaw that’s wrong.

The same problem running in GeoClaw returns err=10^{-15}.

Any ideas?

[ketch]

Thanks for the report. There are a lot of options that could affect this; could you please post a script that reproduces the issue?

[jillelee]

First I saved amdq and apdq data and set output style as

claw.output_style = 3
claw.num_output_times = 30
claw.nstepout = 1

Then load amdq and apdq (for python)

Amdq_python = np.loadtxt('amdq_python.txt')
Apdq_python = np.loadtxt('apdq_python.txt')

and load q

num_output = 31
Q_python = np.empty((num_output, num_equ, num_cell))
t_python_array = np.empty((num_output))
for n in range(num_output):
    sol = solution.Solution(n, path="_output_python")
    Q_python[n,:,:] = sol.q
    t_python_array[n] = sol.t

Diff_python = np.empty((t_steps, num_equ, num_cell+1))
for t in range(t_steps):
    amdq_python = Amdq_python[t,:,1:-1]
    apdq_python = Apdq_python[t,:,1:-1]
    q_python_l = q_python[t,:,:-1]
    q_python_r = q_python[t,:,1:]
    u_python_l = q_python_l[1,:] / q_python_l[0,:]
    u_python_r = q_python_r[1,:] / q_python_r[0,:]
    phi_python_l = q_python_l[1,:] **2 / q_python_l[0,:] + 0.5 * g * q_python_l[0,:]**2
    phi_python_r = q_python_r[1,:] **2 / q_python_r[0,:] + 0.5 * g * q_python_r[0,:]**2
    delta_python_1 = q_python_r[1,:] - q_python_l[1,:]
    delta_python_2 = phi_python_r - phi_python_l
    Diff_python[t, 0,:] = delta_python_1 - (amdq_python[0,:] + apdq_python[0,:])
    Diff_python[t, 1,:] = delta_python_2 - (amdq_python[1,:] + apdq_python[1,:])


abs_max_python = np.empty((t_steps, num_equ))
index_max_python = np.empty((t_steps, num_equ))
abs_Diff_python = abs(Diff_python)
for t in range(t_steps):
    abs_max_python[t,0] = abs_Diff_python[t,0,:].max()
    abs_max_python[t,1] = abs_Diff_python[t,1,:].max()

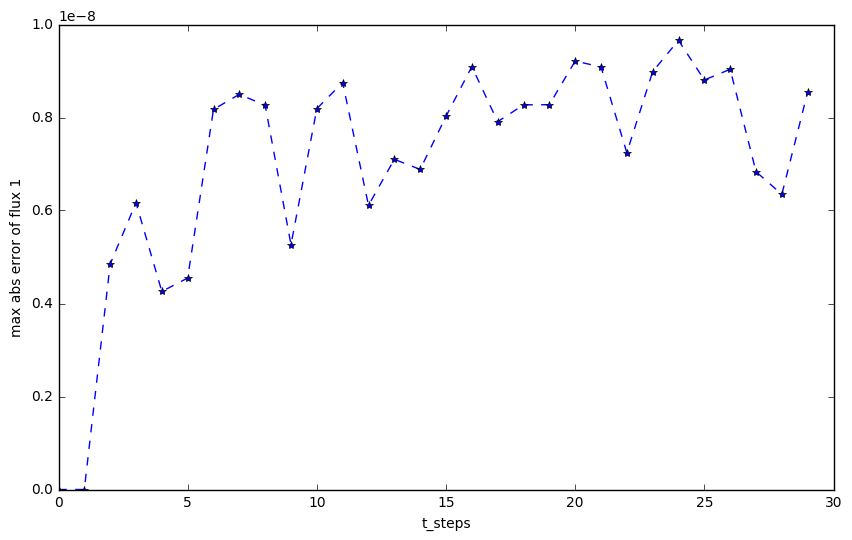
If we plot the biggest error

plt.figure(figsize=(10,6))
plt.plot(np.arange(t_steps), abs_max_python[:,0], '*--')
plt.xlabel('t_steps')
plt.ylabel('max abs error of flux 1')
plt.show()

plt.figure(figsize=(10,6))
plt.plot(np.arange(t_steps), abs_max_python[:,1], 'r*--')
plt.xlabel('t_steps')
plt.ylabel('max abs error of flux 2')
plt.show()

The maximum error of flux1

The maximum error of flux2

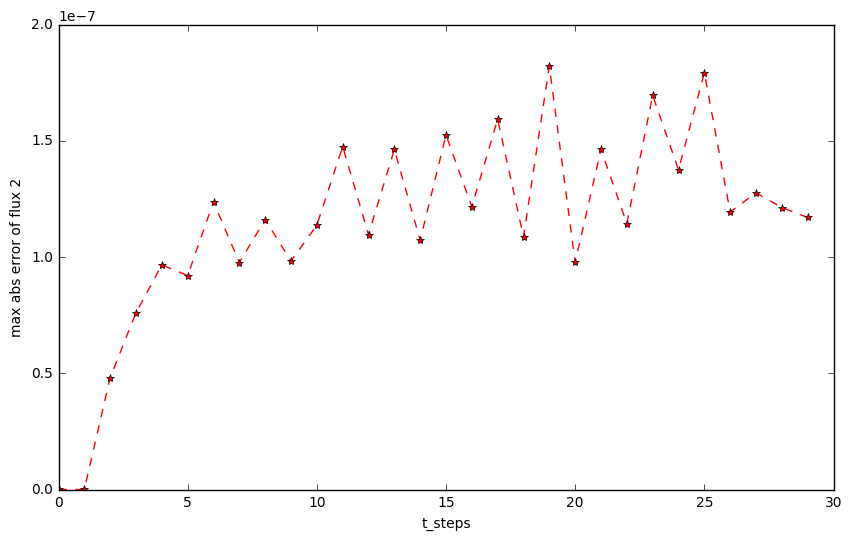
You can see they both at 10^{-8} at least.

If you switch the kernel language from "Python" to "Fortran", you will get the same result.

[ketch]

Thanks, but the important part is the code that generates those text files you're loading. I can't answer your question without knowing what Riemann solver you used, what other solver options were selected, and so forth.

[ketch]

In fact, I'd suggest that you put everything in a single script and avoid writing to text files -- that writing/reading could even be the cause of what you're seeing.

No need to post a lengthy script here; just make a gist and link to it.

[mandli]

@jillelee can you provide maybe a simplified example?

@ketch He has been looking at the shallow water solver and mass conservation. We have been trying to understand why conservation does not seem to be working. He also tried the Euler Roe solver and found the same thing. It's a good idea to check to make sure the output is not degrading the accuracy.

[donnaaboise]

Are these discrepancies on mapped grids?

---

Donna Calhoun Associate Professor Department of Mathematics, MG241A Boise State University 1910 University Drive Boise, ID 83725-1555 (208) 426-3386 http://math.boisestate.edu/~calhoun

On Dec 16, 2017, at 10:06 AM, Kyle Mandli [email protected] wrote:

@jillelee https://github.com/jillelee can you provide maybe a simplified example?

@ketch https://github.com/ketch He has been looking at the shallow water solver and mass conservation. We have been trying to understand why conservation does not seem to be working. He also tried the Euler Roe solver and found the same thing. It's a good idea to check to make sure the output is not degrading the accuracy.

— You are receiving this because you are subscribed to this thread. Reply to this email directly, view it on GitHub https://github.com/clawpack/pyclaw/issues/586#issuecomment-352196141, or mute the thread https://github.com/notifications/unsubscribe-auth/ABV2QQFu9O7mKTD5CT8g64F3gl505jPmks5tA_iegaJpZM4Q_tV4.

[mandli]

No, at least in the current test case. I know there approaches to cut-cells that do not maintain conservation, is there something additional in mapped grids we should be watching out for? We are trying to address a mapped grid problem in the context of 1D however more generally.

[jillelee]

@ketch The riemann solver I used is riemann.shallow_1D_py.shallow_roe_1D. Lines of codes are needed to be added in shallow_roe_1D to save amdq and apdq. To be honest, not just shallow_row_1D solver, other solvers such as shallow_fwave_1d also has this issue.

It seems that there’s something higher up in the PyClaw is wrong, but not the solvers.

[ketch]

@jillelee I'll reemphasize: I'd be very happy to look into this, armed with a complete script that reproduces the bug. Until that's provided, I won't clutter this thread with more comments.

Note that the Riemann solver returns the fluctuations, and you can call it directly. So you don't need to read/write values from disk, and to test the expression you wrote in your first post you don't even need to run a PyClaw simulation. Avoiding both of those will drastically reduce the amount of suspect code. And it would be a step toward verifying your last assertion.