Time Complexity Analysis

[jrtechs]

I just read the paper for this project and it looks amazing and has given me great insight to piece-wise algorithms. I think that it would be amazing if you could include a section to your paper looking at the time complexity of your algorithm.

After running your program against my rather large data set It finds an answer relatively fast for a small number of breaks; but, takes a very long time when it tries to look for more than 5 break points.

What are your thoughts? I would love to help out in any way that I can.

[cjekel]

I'm glad you've found this work interesting! I agree some time complexity would be interesting. Perhaps we could create a surface from a couple machines of 'number of line segments', 'number of data points', and 'convergence tolerance'?

Let's just start with

1. How many data points are in your problem?
2. How many line segments do you plan to go up to?
3. Have you tried both fit() and fitfast()

The largest fit I've done was on ~3 million data points and 15 line segments. I think it took 8 old cores ~24 hours (using fitfast(15, pop=10)).

I just ran a fit with 1.5 million data points using fitfast(5), and it took 5 minutes on my i5-6300u.

---

The least squares fit should be O(b^2 n)

• b: number of line segments + 1
• n: number of data points

I'd image most cases fall into b << n and b^2 < n.

Now when performing fit() the optimization is nonconvex and would run O(b^2 n) several times. With the defaults:

• fit() runs O(b^2 n) at most 50*1,000=50,000 times + a L-BFGS-B polish (15,000 times max)
• fitfast() runs O(b^2 n) at most 2*15,000=30,000 times

So hopefully this provides an idea of how things may scale.

---

I'm very interesting into scaling pwlf for big data.

Some ideas I have right now would be

1. Include a function to run a single l-bfgs-b from an initial guess of breakpoint locations
2. Create a new class to use stochastic gradient descent (SGD). I don't think it'll be possible to use SGD with the current class.

[jrtechs]

@cjekel Thanks for the fast response!

I'm dealing with around 2-3 thousand data points and am partitioning the data into [1...25] line segments. I am following the example from run_opt_to_fund_best_number_of_line_segments.py. I updated it to use use fast fit and that made it run a lot faster.

It would be interesting to make some graphs to show how this thing scales for number of data points and number of line segments. That would probably make a good blog post at the very least. If you want I can generate some graphs for that.

I agree with your initial idea for scaling this for big data; a good greedy heuristic to limit the search space for break-point locations is needed. Datadog did something similar in their piecewise algorithm. That might be worth looking into. However; I don't think it can be transferred to your algorithm nicely. It could possibly be adopted and added as a big data fit option.

What are your thoughts?

[cjekel]

I'm very interested to see how run_opt_to_fund_best_number_of_line_segments.py is working for you. Did you need to tweak the penalty parameter? I'd be interested in reading what you have on the topic. My method is an optimization(optimization(least-squares-fit)) so it's not efficient. I will read and look at what you generate.

In your problem, could the domain of breakpoint locations be restricted to the locations of 2-3 thousand data points? That would reduce the search from infinity to 2-3 thousand possibilities.

I could maybe point you in the direction of other implementations to do variable line segment continuous piecewise fitting.

[cjekel]

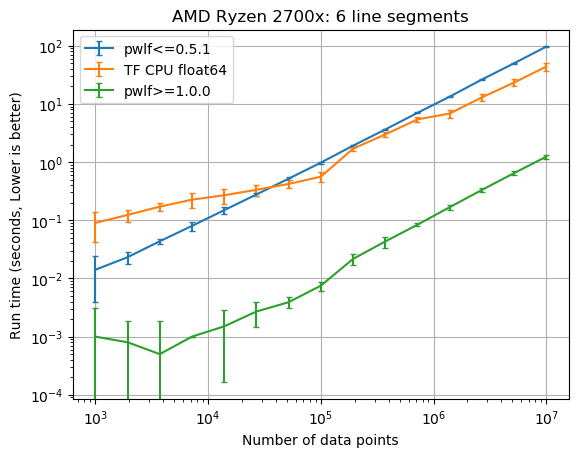
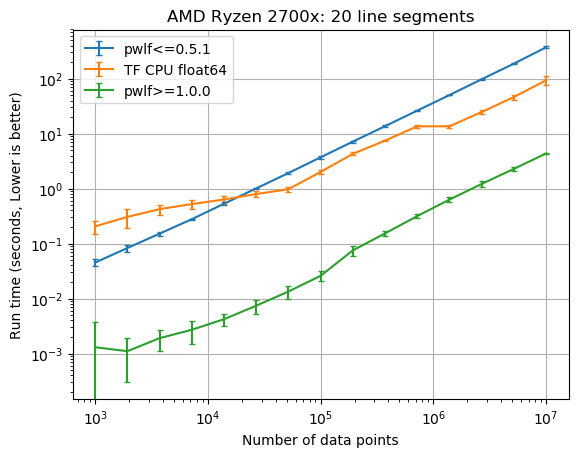
This post shows how the run time of fit_with_breaks varies with the number of data points, however it doesn't show how fit or fitfast vary with the number of line segments.

[jrtechs]

@cjekel I love your new blog post comparing the run times with TensorFlow.

I ended up improving the performance in my project by using a sliding window time series segmentation approach. For my particular application this ended up working better than fitting low degree polynomials.

@cjekel are the performance graphs something you are considering incorporating into your paper? It would be neat to include a quick section about the theoretical and empirical performances of the algorithm with respect to the number of segments and number of points.

[cjekel]

I'm glad you like the post. I still need to decide how to include this in the paper.

---

I ended up improving the numpy performance by almost two order of magnitudes in an upcoming pwlf.__version__==1.0.0 release. It changes how the matrix assembly is performed, and removes sorting. I'll need to adjust the paper accordingly. But I was pretty excited to see these results.