blog
blog copied to clipboard
camsong
JavaScript 浮点数陷阱及解法
原发于知乎专栏：https://zhuanlan.zhihu.com/ne-fe
众所周知，JavaScript 浮点数运算时经常遇到会 0.000000001 和 0.999999999 这样奇怪的结果，如 0.1+0.2=0.30000000000000004、1-0.9=0.09999999999999998，很多人知道这是浮点数误差问题，但具体就说不清楚了。本文帮你理清这背后的原理以及解决方案，还会向你解释JS中的大数危机和四则运算中会遇到的坑。
浮点数的存储
首先要搞清楚 JavaScript 如何存储小数。和其它语言如 Java 和 Python 不同，JavaScript 中所有数字包括整数和小数都只有一种类型 — Number。它的实现遵循 IEEE 754 标准，使用 64 位固定长度来表示，也就是标准的 double 双精度浮点数（相关的还有float 32位单精度）。计算机组成原理中有过详细介绍，如果你不记得也没关系。
这样的存储结构优点是可以归一化处理整数和小数，节省存储空间。
64位比特又可分为三个部分：
- 符号位S：第 1 位是正负数符号位（sign），0代表正数，1代表负数
- 指数位E：中间的 11 位存储指数（exponent），用来表示次方数
- 尾数位M：最后的 52 位是尾数（mantissa），超出的部分自动进一舍零
实际数字就可以用以下公式来计算：

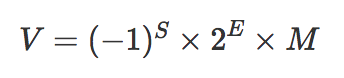
注意以上的公式遵循科学计数法的规范，在十进制是为0<M<10，到二进行就是0<M<2。也就是说整数部分只能是1，所以可以被舍去，只保留后面的小数部分。如 4.5 转换成二进制就是 100.1，科学计数法表示是 1.001*2^2，舍去1后 M = 001。E是一个无符号整数，因为长度是11位，取值范围是 0~2047。但是科学计数法中的指数是可以为负数的，所以再减去一个中间数 1023，[0,1022]表示为负，[1024,2047] 表示为正。如4.5 的指数E = 1025，尾数M为 001。
最终的公式变成：
所以 4.5 最终表示为（M=001、E=1025）：

(图片由此生成 http://www.binaryconvert.com/convert_double.html)
下面再以 0.1 例解释浮点误差的原因， 0.1 转成二进制表示为 0.0001100110011001100(1100循环)，1.100110011001100x2^-4，所以 E=-4+1023=1019；M 舍去首位的1，得到 100110011...。最终就是：

转化成十进制后为 0.100000000000000005551115123126，因此就出现了浮点误差。
为什么 0.1+0.2=0.30000000000000004？
计算步骤为：
// 0.1 和 0.2 都转化成二进制后再进行运算
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.0100110011001100110011001100110011001100110011001100111
// 转成十进制正好是 0.30000000000000004
为什么 x=0.1 能得到 0.1？
恭喜你到了看山不是山的境界。因为 mantissa 固定长度是 52 位，再加上省略的一位，最多可以表示的数是 2^53=9007199254740992，对应科学计数尾数是 9.007199254740992，这也是 JS 最多能表示的精度。它的长度是 16，所以可以使用 toPrecision(16) 来做精度运算，超过的精度会自动做凑整处理。于是就有：
0.10000000000000000555.toPrecision(16)
// 返回 0.1000000000000000，去掉末尾的零后正好为 0.1
// 但你看到的 `0.1` 实际上并不是 `0.1`。不信你可用更高的精度试试：
0.1.toPrecision(21) = 0.100000000000000005551
大数危机
可能你已经隐约感觉到了，如果整数大于 9007199254740992 会出现什么情况呢？
由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1，这就是能表示的最大整数。但你并不能这样计算这个数字，因为从 2^1024 开始就变成了 Infinity
> Math.pow(2, 1023)
8.98846567431158e+307
> Math.pow(2, 1024)
Infinity
那么对于 (2^53, 2^63) 之间的数会出现什么情况呢？
-
(2^53, 2^54)之间的数会两个选一个，只能精确表示偶数 -
(2^54, 2^55)之间的数会四个选一个，只能精确表示4个倍数 - ... 依次跳过更多2的倍数
下面这张图能很好的表示 JavaScript 中浮点数和实数（Real Number）之间的对应关系。我们常用的 (-2^53, 2^53) 只是最中间非常小的一部分，越往两边越稀疏越不精确。
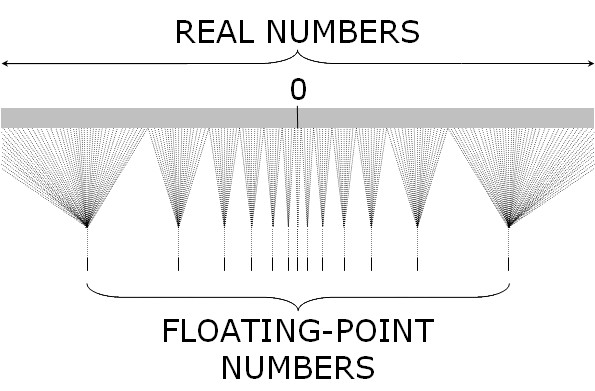
在淘宝早期的订单系统中把订单号当作数字处理，后来随意订单号暴增，已经超过了
9007199254740992，最终的解法是把订单号改成字符串处理。
要想解决大数的问题你可以引用第三方库 bignumber.js，原理是把所有数字当作字符串，重新实现了计算逻辑，缺点是性能比原生的差很多。所以原生支持大数就很有必要了，现在 TC39 已经有一个 Stage 3 的提案 proposal bigint，大数问题有望彻底解决。在浏览器正式支持前，可以使用 Babel 7.0 来实现，它的内部是自动转换成 big-integer 来计算，要注意的是这样能保持精度但运算效率会降低。
toPrecision vs toFixed
数据处理时，这两个函数很容易混淆。它们的共同点是把数字转成字符串供展示使用。注意在计算的中间过程不要使用，只用于最终结果。
不同点就需要注意一下：
-
toPrecision是处理精度，精度是从左至右第一个不为0的数开始数起。 -
toFixed是小数点后指定位数取整，从小数点开始数起。
两者都能对多余数字做凑整处理，也有些人用 toFixed 来做四舍五入，但一定要知道它是有 Bug 的。
如：1.005.toFixed(2) 返回的是 1.00 而不是 1.01。
原因： 1.005 实际对应的数字是 1.00499999999999989，在四舍五入时全部被舍去！
解法：使用专业的四舍五入函数 Math.round() 来处理。但 Math.round(1.005 * 100) / 100 还是不行，因为 1.005 * 100 = 100.49999999999999。还需要把乘法和除法精度误差都解决后再使用 Math.round。可以使用后面介绍的 number-precision#round 方法来解决。
解决方案
回到最关心的问题：如何解决浮点误差。首先，理论上用有限的空间来存储无限的小数是不可能保证精确的，但我们可以处理一下得到我们期望的结果。
数据展示类
当你拿到 1.4000000000000001 这样的数据要展示时，建议使用 toPrecision 凑整并 parseFloat 转成数字后再显示，如下：
parseFloat(1.4000000000000001.toPrecision(15)) === 1.4 // True
封装成方法就是：
function strip(num, precision = 15) {
return +parseFloat(num.toPrecision(precision));
}
为什么选择 15 做为默认精度？这是一个经验的选择，一般选15就能解决掉大部分0001和0009问题，而且大部分情况下也够用了，如果你需要更精确可以调高。
数据运算类
对于运算类操作，如 +-*/，就不能使用 toPrecision 了。正确的做法是把小数转成整数后再运算。以加法为例：
/**
* 精确加法
*/
function add(num1, num2) {
const num1Digits = (num1.toString().split('.')[1] || '').length;
const num2Digits = (num2.toString().split('.')[1] || '').length;
const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));
return (num1 * baseNum + num2 * baseNum) / baseNum;
}
以上方法能适用于大部分场景。遇到科学计数法如 2.3e+1（当数字精度大于21时，数字会强制转为科学计数法形式显示）时还需要特别处理一下。
能读到这里，说明你非常有耐心，那我就放个福利吧。遇到浮点数误差问题时可以直接使用 https://github.com/dt-fe/number-precision
完美支持浮点数的加减乘除、四舍五入等运算。非常小只有1K，远小于绝大多数同类库（如Math.js、BigDecimal.js），100%测试全覆盖，代码可读性强，不妨在你的应用里用起来！
参考
- Double-precision floating-point format
- What Every Programmer Should Know About Floating-Point Arithmetic
- Why Computers are Bad at Algebra | Infinite Series
- Is Your Model Susceptible to Floating-Point Errors?
当然写这篇文章是为了招聘！！！
阿里巴巴大数据前端部门诚招前端攻城狮。不要犹豫，万一通过了呢。 简历发过来
[email protected]
@camsong 感谢作者的分享，文章很不错 👍 其中 大数字危机 一节中：
由于 M（应该是笔误 ❓） 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1。这就是能表示的最大整数。
这句有点困惑，指数位最大值为 2047，减去 1023 后应该是 1024 吧，所以最大能表示的数为 2^1024 - 1 ？
JavaScript能表示并进行精确算术运算的整数范围为：正负2的53次方；超过范围的，无法给出精确计算结果，您文章给出的配图： JavaScript 中浮点数和实数（Real Number）之间的对应关系 也解释了这一点。
Math.pow(2, 53)
-> 9007199254740992
Math.pow(2, 53) + 1
-> 9007199254740992
Math.pow(2, 53) + 2
-> 9007199254740994
这个段代码也验证了：(2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数。而这一点应该也可以作为回答知乎问题的理由之一吧：javascript 里最大的安全的整数为什么是2的53次方减一？
666，感谢分享干货，已推荐到 SegmentFault 头条 (๑•̀ㅂ•́)و✧ 链接如下：https://segmentfault.com/p/1210000011570610
嗯嗯，那什么情况是strip实现不了，必须用精确加减乘除的吗？我感觉我能想到的计算需求，只要计算完成之后strip一下就正确了，就不需要加减乘除那几个函数了~
@shoung6 外部传入的“异常”数据需要展现的时候。如后端接口返回 3.4500000001，前端要格式化后展示的情况。浮点数异常对 Java、Python、Ruby 等语言都适用。
文中 strip 会把精度降到 10^12，但 JS 本身的精度可以到 2^53。当你做多次计算时当初的小误差，结果可能就有大不同。还是看场景吧，如果你数字很小，最后 strip 一下也是可以的
想请教个问题： 文中提到，10进制的0.1，转成二进制结果是0.0001100110011001100（无限循环）， 既然是无限循环，根据二进制转十进制的公式， 结果应该是：0+0+0+1/16 +1/32+0+0+1/256+1/512+......+.........， 最终结果应该小于0.1才对（因为后面肯定加不完，等于少加了一些），但结果确是0.100000000000000005551115123126， 这个数字明显大于0.1，很不解，是我理解的不对吗，求解啊
还有个问题：
Math.pow(2,53)+0 >>9007199254740992
Math.pow(2,53)+1 >>9007199254740992
以上可以说明2^53-2^54之间，每两个选一个，但接下来：
Math.pow(2,53)+2 >>9007199254740994（注意这个值）
Math.pow(2,53)+3 >>9007199254740996
Math.pow(2,53)+4 >>9007199254740996，
这就有问题了，+3时应该和+2保持一致啊，但是程序的结果却很意外，并不是每2个选一个，
求解，先感激下！
@mmmmmaster 我来回答一下这两个问题吧 😋
① 十进制的 0.1 转换成二进制后，结果的确是 0.0001100110011001100（无限循环），这个二进制再进行 64 位浮点数存储得到：0011111110111001100110011001100110011001100110011001100110011010 ，然后再将这个64位二进制转换回十进制的时候，得到的就是：0.100000000000000005551115123126。这个转换可以通过在线网站：http://www.binaryconvert.com/convert_double.html 进行
②首先我们要知道 [-2^53, +2^53] 这个范围是称为 safe integers，超出这个范围的数字，就是 unsafe integers。对于对于 (2^53, 2^63) 之间的数会出现什么情况呢？
(2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数 (2^54, 2^55) 之间的数会四个选一个，只能精确表示4个倍数 ... 依次跳过更多2的倍数
所以我们看到 (2^53, 2^54) 范围的数字，都是间隔 2 的。
然后我们还要了解到不是 safe integers 的数字，计算结果不能确保其正确性。所以你提到的那几个计算中有些正确，有些不正确。
第二个问题关键在于不要混淆这两个概念即可。
最后，@camsong 这么理解对吧 😂
@YingshanDeng
感谢大哥解答！
第一个问题，从在线网站上转完，确实结果是0.100000000000000005551115123126，但是如果从我们人类的角度来计算，这个结果应该是偏小的（毕竟无限循环加不完啊），不知道误差原因所在。。
第二个问题，如果从超出安全范围则计算结果不准确来考虑，程序吐出那样的结果确实是情有可原的，可理解！
最后， @camsong ，这么理解对吧 :joy:
@mmmmmaster 根据我的理解，来解释一下你提到的 0.1 “误差偏大”问题 😀
我们知道十进制 0.1 转换成二进制的时候，小数点后是 0011 循环，然后我们再看看 0.1 用64位二进制表示成：0011111110111001100110011001100110011001100110011001100110011010 注意到尾数最后八位：10011010，我们把正常循环写出来是 100110011，对比之下很明显，有一个四舍五入进位，所以这就导致误差偏大
终于把我关于 toFixed 的疑惑解释清楚了，可惜公司看不到图片，回家在看一遍储存的问题。感觉 number-precision 就是我第一版修正计算精度的思路，不过我们测试还是不满意效果，最终引入了一个大小和精度介于 number-precision 和 bignumber.js 之间的库 big.js
因为 mantissa 固定长度是 52 位，再加上省略的一位，最多可以表示的数是 2^53=9007199254740992
大神，省略的一位是什么意思呢
@guitong
下面再以 0.1 例解释浮点误差的原因， 0.1 转成二进制表示为 0.0001100110011001100(1100循环)，1.100110011001100x2^-4，所以 E=-4+1023=1019；M 舍去首位的1，得到 100110011...。
非0数用十进制的科学计数法表示时首位为 1~9，用二进制表示时首位只能是 1，所以就约定把首位这个 1 省去。
有一个疑问，为何C语言中，同样64位双精度的0.1 + 0.2 能计算到结果呢？不知博主是否知道 举例：
double a = 0.1;
double b = 0.2;
printf("%lf",a+b); // 0.3
谢谢！
At 2018-03-20 22:47:52, "robberfree" [email protected] wrote:
@WuHuaJi0 你printf的时候指定了输出格式，所以会截取。
— You are receiving this because you are subscribed to this thread. Reply to this email directly, view it on GitHub, or mute the thread.
@WuHuaJi0
%f的完整格式应该是%a.bf
b是精度，默认精度是6。
你想输出更多精度的浮点数
直接把精度位数提高就行
int main()
{
double a=0.1;
double b=0.2;
double c=a+b;
printf("%.17f",c);
}
这个输出是 0.30000000000000004 c语言的文档应该有关于这些的描述。
最大安全整数
是指在浮点数存储机制中，利用“尾数的有限的2进制位”能够与实数建立一对一映射的最大整数。
JS中，最大安全整数是 2^53 - 1。证明如下：
2^53的2进制科学计数法表示：1E2^53，尾数M是52个0，指数E=53。
2^53 的保存形式：S=0 E=53 M=1.000000...0000(小数点后一共53个0)
注意：小数点后53个0，但M只有52位，因此最后一个0会被丢弃，所以
2^53 的保存形式：S=0 E=53 M=1.000000...000(小数点后一共52个0，丢失一位)
2^53-1的保存形式：S=0 E=52 M=1.111111....111(小数点后52个1）
2^53-2的保存形式：S=0 E=52 M=1.0111111....110(小数点后51个1,一个0）
依次倒推，可以一直推到0，因此，实数整数和2进制位存在11映射关系。
但当数字超过2^53时，如何表示呢？
只能通过扩大指数E来实现。
假设要表示 2^53+1这个数。
2^53+1的保存形式：S=0 E=53 M=1.000...001(小数点后52个0，,1个1)
但因为M只能保存52位，最后的这个1保存不了，会丢失。因此
2^53+1最终的保存形式：S=0 E=53 M=1.000000...000(小数点后一共53个0）
这样一来，2^53和2^53+1的保存形式完全一样了！从而从2^53开始，实数和2进制位的不再是11对应关系。
在展开这个2进制位时，JS知道有1位被丢弃，因此会在最后的结果末尾添加一个0(对于2^54就是在末尾加两个0)。由此，对于2^53+n的数而言，只有那些2进制形式的1可以进位到52位以内的数可以被表示——也就是末尾是0的数，其余末尾是1的数都无法表示。
演示如下：
假设我们要表示(2^53)+1---(2^53)+5的数：
> Math.pow(2, 53)+0
9007199254740992 --> E=53,M=1.000...0000(53个0,实际存储52个0)
> Math.pow(2, 53)+1
9007199254740992 --> E=53,M=1.000...0001(52个0+1个1，实际存储52个0)
> Math.pow(2, 53)+2
9007199254740994 --> E=53,M=1.000...0010(51个0+1个1+1个0,实际存储51个0+1个1)
> Math.pow(2, 53)+3
9007199254740994 --> E=53,M=1.000...0011(51个0+2个1,实际存储51个0+1个1)
> Math.pow(2, 53)+4
9007199254740996 --> E=53,M=1.000...0100(50个0+1个1+2个0,实际存储50个0+1个1+1个0)
> Math.pow(2, 53)+5
9007199254740996 -->E=53,M=1.000...0101(50个0+1个1+1个0,实际存储50个0+1个1+1个0)
可以看到，正是因为M是有限的，导致从2^53开始所有2进制形式中以1结尾的数与它前一个数的保存形式完全相同，从而形成这种现象。
结论：JS的最大安全整数是 2^53-1
@roro4ever 感谢分享，但是我在v8（chrome和node的REPL环境下）下测试了Math.pow(2, 53) + 3的到的结果是9007199254740996，而不是9007199254740994。开始我以为是v8的处理方式不同，我又在python v2.7下测试，得到的结果还是9007199254740996，在java中也是得到9007199254740996
于是，我按照真实计算得出的结果继续算下去：
> Math.pow(2, 53) + 6
9007199254740996 --> E=53,M=1.000...0110 (50个0+2个1+1个0,实际存储50个0+2个1)
> Math.pow(2, 53) + 7
9007199254741000 --> E=53,M=1.000...0111 (50个0+2个1+1个1,实际存储49个0+1个1+2个0)
> Math.pow(2, 53) + 8
9007199254741000 --> E=53,M=1.000...1100 (49个0+2个1+2个0,实际存储49个0+2个1+1个0)
> Math.pow(2, 53) + 9
9007199254741000 --> E=53,M=1.000...1101 (49个0+2个1+1个0+1个1,实际存储49个0+2个1+1个0)
> Math.pow(2, 53) + 10
9007199254741002 --> E=53,M=1.000..01110 (49个0+3个1+1个0,实际存储49个0+3个1)
> Math.pow(2, 53) + 11
9007199254741004 --> E=53,M=1.000..01111 (49个0+3个1+1个1,实际存储48个0+1个1+3个0)
我觉得算到这里大概可以猜测原因是这样的： 当最后一位是1并且多出的第53位是1时，会进1位，而不是直接舍弃。
function strip(num, precision = 12) {
return +parseFloat(num.toPrecision(precision));
}
这个加号是不是多余的??? parseFloat本身就是返回数字
function strip(num, precision = 12) { return +parseFloat(num.toPrecision(precision)); }这个加号是不是多余的??? parseFloat本身就是返回数字
同问 我也觉得不需要+ parseFloat得到的就是Number类型啊 不需要转换了
@camsong @YingshanDeng 感谢大神分享， 有个疑惑，按照公式，指数最大应该是1024，最大的数不应该是2^2014*1.111111(小数后52个1, 2进制)吗？
写了段代码测试下。
Number(0.1+0.2).toString(2) \\ "0.0100110011001100110011001100110011001100110011001101"
Number(0.3).toString(2) \\"0.010011001100110011001100110011001100110011001100110011"
0.1 + 0.2 \\ 0.30000000000000004
Number(0.1+0.2).toString(2).length \\54
1025.88*100 // 102588.00000000001
add(1025.88, 3.74) //1029.6200000000001
qwq
function strip(num, precision = 12) { return +parseFloat(num.toPrecision(precision)); }这个加号是不是多余的??? parseFloat本身就是返回数字
同问 我也觉得不需要+ parseFloat得到的就是Number类型啊 不需要转换了
我猜测是避免后续操作需要转换 例 ：+parseFloat((6.35 * 1.5).toPrecision(12)) // 9.525 +parseFloat((6.35 * 1.5).toPrecision(12)).toFixed(2) // 9.53
为什么 Number.MAX_VALUE 最多只有 2^1023
Math.pow(2, 1023)
> 8.98846567431158e+307
Math.pow(2, 1024)
> Infinity
Number.MAX_VALUE
> 1.7976931348623157e+308
根据下图，我认为最大因该是 1023(最大的 E) + 53 = 1076 次方
为什么 Number.MAX_VALUE 最多只有 2^1023
Math.pow(2, 1023) > 8.98846567431158e+307 Math.pow(2, 1024) > Infinity Number.MAX_VALUE > 1.7976931348623157e+308根据下图，我认为最大因该是 1023(最大的 E) + 53 = 1076 次方
公式中的M要符合科学计数法，也就是在二进制下M只能是1≤|M|<2的数
为什么 Number.MAX_VALUE 最多只有 2^1023
Math.pow(2, 1023) > 8.98846567431158e+307 Math.pow(2, 1024) > Infinity Number.MAX_VALUE > 1.7976931348623157e+308根据下图，我认为最大因该是 1023(最大的 E) + 53 = 1076 次方
公式中的M要符合科学计数法，也就是在二进制下M只能是1≤|M|<2的数
thanks, 明白了
Math.pow(2, 1023) * 1.999999999999999
> 1.797693134862315e+308
@camsong 楼主采用toPrecision而不是toFixed来解决问题，但是toFixed出现的舍入问题在toPrecision一样会出现啊，比如1.005.toFixed(2)结果是"1.00"，但是1.005.toPrecision(3)的结果也同样是"1.00"，能说一下为什么抛弃toFixed而采用toPrecision吗？
想请教个问题： 文中提到，10进制的0.1，转成二进制结果是0.0001100110011001100（无限循环）， 既然是无限循环，根据二进制转十进制的公式， 结果应该是：0+0+0+1/16 +1/32+0+0+1/256+1/512+......+.........， 最终结果应该小于0.1才对（因为后面肯定加不完，等于少加了一些），但结果确是0.100000000000000005551115123126， 这个数字明显大于0.1，很不解，是我理解的不对吗，求解啊
这段时间专门研究过“浮点数”这一块，大概说一下我的理解：十进制里面有我们熟悉的“四舍五入”，二进制里面也有类似的机制，你可以理解为“0 舍 1 入”。有舍有入，那么舍/入之后的结果也有两种可能。这篇文章所描述的十进制 0.1 转为双精度二进制表示的时候，超出所取精度的那一位刚好是 1，这时候应该做“入”的操作，结果当然就比实际值要略大一些。看你的描述，你在十进制加法那里直接把后面的数忽略了，舍入操作不是这样子的。
因为 mantissa 固定长度是 52 位，再加上省略的一位，最多可以表示的数是 2^53=9007199254740992，对应科学计数尾数是 9.007199254740992，这也是 JS 最多能表示的精度。它的长度是 16，所以可以使用 toPrecision(16) 来做精度运算，超过的精度会自动做凑整处理。
“为什么 x=0.1 能得到 0.1？”这一块有一些不明白的地方，能否指点一下？ 0.1 是 JavaScript 中的 Number 类型，用的是 IEEE 754 双精度格式，那么为什么不是直接在二进制下讨论它的精度，而是转换为十进制之后再讨论它的精度呢？而且“JS 最多能表示的精度。它的长度是 16”，0.1+0.2 的结果默认就是 17位，这不是矛盾吗？
在淘宝早期的订单系统中把订单号当作数字处理，后来随意订单号暴增，已经超过了 9007199254740992，最终的解法是把订单号改成字符串处理
9007199254740992 这个数字是怎么来的，IEEE 754 双精度格式下的有符号整数最大值不是这个吧。。。有点懵了
0.1 用64位二进制表示成：0011111110111001100110011001100110011001100110011001100110011010 末位为什么是0
在淘宝早期的订单系统中把订单号当作数字处理，后来随意订单号暴增，已经超过了 9007199254740992，最终的解法是把订单号改成字符串处理
9007199254740992 这个数字是怎么来的，IEEE 754 双精度格式下的有符号整数最大值不是这个吧。。。有点懵了
9007199254740992 (= Math.pow(2, 53)) 是 尾数部分所能表示的最大精确的数值; js中最大的安全数 Number.MAX_SAFE_INTEGER = 9007199254740991; 简单来说, 在这个范围内的数, 用 52 + 1 个坑 ,可以把这个数描述清楚, 凡是超过这个范围, 就会自动的进行四舍五入处理, 不能表示想要的精确值;
var a = 9007199254740991; // a = 9007199254740991 var b = 9007199254740993; // b = 9007199254740992 var c = 9007199254740995; // c = 9007199254740996
因为 mantissa 固定长度是 52 位，再加上省略的一位，最多可以表示的数是 2^53=9007199254740992，对应科学计数尾数是 9.007199254740992，这也是 JS 最多能表示的精度。它的长度是 16，所以可以使用 toPrecision(16) 来做精度运算，超过的精度会自动做凑整处理。
“为什么 x=0.1 能得到 0.1？”这一块有一些不明白的地方，能否指点一下？ 0.1 是 JavaScript 中的 Number 类型，用的是 IEEE 754 双精度格式，那么为什么不是直接在二进制下讨论它的精度，而是转换为十进制之后再讨论它的精度呢？而且“JS 最多能表示的精度。它的长度是 16”，0.1+0.2 的结果默认就是 17位，这不是矛盾吗？
这个的确很迷惑
与原文中
如：1.005.toFixed(2) 返回的是 1.00 而不是 1.01。
原因： 1.005 实际对应的数字是 1.00499999999999989，在四舍五入时全部被舍去！
这里矛盾
比如 小数 1.105 1.105.toPrecision(16) 为 "1.105000000000000" 那么1.105.toFixed(2)应该是1.11 实际结果却是 1.10 （Chrome 73.0.3683.86） 然后我们将 有效数位提高到32位 1.105.toPrecision(32) 为 "1.1049999999999999822364316059975" 所以解释了toFixed函数遇5不入的问题
所以JS 最多能表示的精度不是16 而0.1+0.2=0.30000000000000004 仅仅能说明了JS中的Number值 默认取用toFixed或toPrecision处理过
一些随机的例子
300.73-70 // 230.73000000000002
2-0.14 // 1.8599999999999999
0.1+0.2 // 0.30000000000000004
1.05-1 // 0.050000000000000044
300.73-300 // 0.7300000000000182
对于大于1的浮点数 取toPrecision(17) 对于小于1的浮点数 取toPrecision(16)或toPrecision(17)
暂时这样
请教一下，既然0.1通过toPrecision(16)来做精度运算，最终结果为0.1；那么为啥0.1 + 0.2的结果0.30000000000000004并没有按照toPrecision(16)来做精度运算，而是toPrecision(17)呢？
(0.1 + 0.2).toPrecision(16) // 0.3000000000000000
(0.1 + 0.2).toPrecision(17) // 0.30000000000000004
function add(num1, num2) {
const num1Digits = (num1.toString().split('.')[1] || '').length;
const num2Digits = (num2.toString().split('.')[1] || '').length;
const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));
return (num1 * baseNum + num2 * baseNum) / baseNum;
}
add(20.24, 10.12) // 30.359999999999996
这个 add 好像有问题啊
function add(num1, num2) { const num1Digits = (num1.toString().split('.')[1] || '').length; const num2Digits = (num2.toString().split('.')[1] || '').length; const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits)); return (num1 * baseNum + num2 * baseNum) / baseNum; } add(20.24, 10.12) // 30.359999999999996这个
add好像有问题啊
确实有问题，num1 * baseNum 这一步还是会有浮点数问题
0.1 用64位二进制表示成：0011111110111001100110011001100110011001100110011001100110011010 末位为什么是0
末位在未被截取前是0011，第五十三位是1所以进一就变成了0101
function add(num1, num2) { const num1Digits = (num1.toString().split('.')[1] || '').length; const num2Digits = (num2.toString().split('.')[1] || '').length; const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits)); return (num1 * baseNum + num2 * baseNum) / baseNum; } add(20.24, 10.12) // 30.359999999999996这个
add好像有问题啊确实有问题，num1 * baseNum 这一步还是会有浮点数问题
推荐： calculate-asmd
function add(num1, num2) { const num1Digits = (num1.toString().split('.')[1] || '').length; const num2Digits = (num2.toString().split('.')[1] || '').length; const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits)); return (num1 * baseNum + num2 * baseNum) / baseNum; } add(20.24, 10.12) // 30.359999999999996这个
add好像有问题啊
推荐： calculate-asmd
function add(num1, num2) { const num1Digits = (num1.toString().split('.')[1] || '').length; const num2Digits = (num2.toString().split('.')[1] || '').length; const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits)); return (num1 * baseNum + num2 * baseNum) / baseNum; } add(20.24, 10.12) // 30.359999999999996这个
add好像有问题啊确实有问题，num1 * baseNum 这一步还是会有浮点数问题
直接整数和小数部分转字符串连接，不够的exponent后面补'0'即可修复。 比如，20.24 和 1.1，最大 exponent = 2，那么 20.24字符串为"2024", 1.1则为"110"，然后 parseInt 相加，结果再乘以 pow(10, -2) 即可。
有一点不是很明白，按照16位精度计算的话 0.1 + 0.2 应该也会像 0.1 一样被忽略掉吧
(0.1 + 0.2 ).toPrecision(16)
// '0.3000000000000000'
(0.1 + 0.2 ).toPrecision(17)
// '0.30000000000000004'
(0.1).toPrecision(17)
// '0.10000000000000001'
有一点不是很明白，按照16位精度计算的话 0.1 + 0.2 应该也会像 0.1 一样被忽略掉吧
(0.1 + 0.2 ).toPrecision(16) // '0.3000000000000000' (0.1 + 0.2 ).toPrecision(17) // '0.30000000000000004' (0.1).toPrecision(17) // '0.10000000000000001'
- 大于一的浮点数，精度默认为16
- 小于一的浮点数，精度默认为16或者17 普遍的规律，具体原理应该得看js引擎的底层实现源码了
有一点不是很明白，按照16位精度计算的话 0.1 + 0.2 应该也会像 0.1 一样被忽略掉吧
(0.1 + 0.2 ).toPrecision(16) // '0.3000000000000000' (0.1 + 0.2 ).toPrecision(17) // '0.30000000000000004' (0.1).toPrecision(17) // '0.10000000000000001'
在 17 位精度范围内存在非 0 的数，所以以 17 位显示，否则精度到非 0 的那位数
假如
0.1 + 0.2 = 0.30040000000000000 004409
得到的数应该是 0.3004。
也就是说默认的小数精度是 17 位
function add(num1, num2) { const num1Digits = (num1.toString().split('.')[1] || '').length; const num2Digits = (num2.toString().split('.')[1] || '').length; const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits)); return (num1 * baseNum + num2 * baseNum) / baseNum; } add(20.24, 10.12) // 30.359999999999996这个
add好像有问题啊确实有问题，num1 * baseNum 这一步还是会有浮点数问题
直接整数和小数部分转字符串连接，不够的exponent后面补'0'即可修复。 比如，20.24 和 1.1，最大 exponent = 2，那么 20.24字符串为"2024", 1.1则为"110"，然后 parseInt 相加，结果再乘以 pow(10, -2) 即可。
这样还是不行，最后乘以 pow(10, -2) 的时候仍然会有精度问题，需要除以pow(10, 2)
@camsong 有个问题不解，尾数52位，超出的部分会进1舍0，那么
> Math.pow(2, 53)+0
9007199254740992 --> E=53,M=1.000...0000
(53个0,实际存储52个0)
> Math.pow(2, 53)+1
9007199254740992 --> E=53,M=1.000...0001
(52个0+1个1，实际存储应该是进1舍0后得到，51个0，1个1)
那这样就得不到
Math.pow(2, 53) === Math.pow(2, 53) + 1
很困惑。。。
@YingshanDeng @mmmmmaster @Rennzh 关于尾数超出部分的处理并不是进1舍0，IEEE-754 舍入模式有多种，题主文章中有提到 2^53 - 2^54 之间的数都是“偶数”对，即2个数取一个，所以这里的舍入模式应该是 “就近舍入”，当有两个最接近的可表示的值时首选“偶数”值。
参见：
@roro4ever 👍
> Math.pow(2, 53)+3
9007199254740994 --> E=53,M=1.000...0011(51个0+2个1,实际存储51个0+1个1)
there is small error in Math.pow(2, 53)+3, it should be 9007199254740996 :smile:,
By the way, I want to confirm the last 52 bits is named mantissa or fraction, I find it is named fraction in wikimedia and fraction is also quoted in speech by a TC39 member from BigInts in JavaScript:A case study in TC39
.
@camsong
我在写JavaScript之0.1+0.2=0.30000000000000004的计算过程的时候发现一个问题：
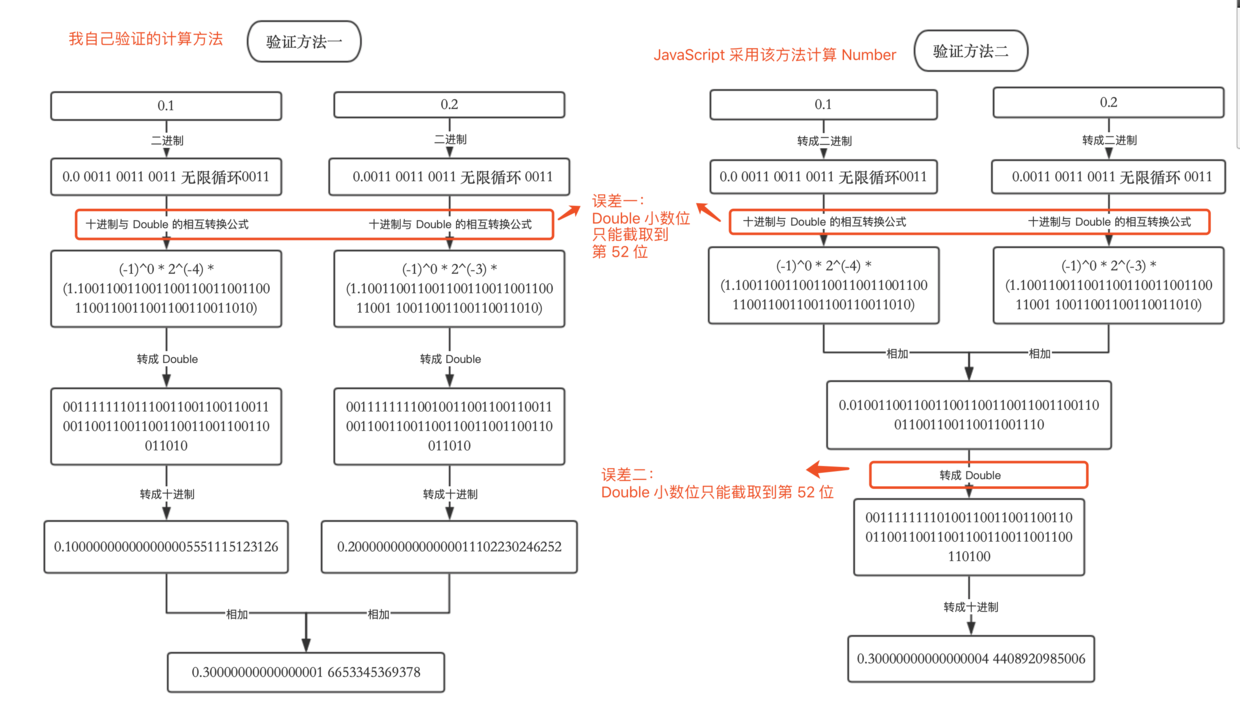
如果我的「验证方法一」没问题的话，为什么 JS 会采用误差更大的「验证方法二」？ 恳请大佬们解惑
为什么 x=0.1 能得到 0.1？ 这一块。您说的是：
因为 mantissa 固定长度是 52 位，再加上省略的一位，最多可以表示的数是 2^53=9007199254740992，对应科学计数尾数是 9.007199254740992，这也是 JS 最多能表示的精度。它的长度是 16，
- mantissa 固定长度是 52 位，加上省略的 1位, 二进制里就是 53个 1，转换为 10进制，所以最多可以表示的是 2^ 53 - 1 = 9007199254740991
- 虽说算出了精度的位数是 16位，但有些16位的小数转换 ，肯定还会出现误差，我找到了一个 0.9007199254740999，控制台输入得到这样的结果
为什么会有精度丢失? 什么时候发生精度丢失?
本次讨论主要解决两个问题:
-
使用 JS 编程时为什么会出现精度丢失?
-
使用 JS 编程时什么时候发生精度丢失? 即
Number.MAX_SAFE_INTEGER的值是多少?
1. 使用 JS 编程时为什么会出现精度丢失?
建议先看下本 issue 里作者对于 JS 里怎么存储数字的介绍, 这里简述一下其原理, 只是为了便于解释精度丢失的议题:
JS 里用 64 bits 的空间存储数字, 使用 IEEE-754格式存储和解析数字, 用的是类似科学技术法的方式表示的数字. 比如: 123456 = 1.23456 * 10^5, 这里的 1.23456 就是有效数字, 10^5 的 5是指数. 可以看出来: 如果我们实现定义好使用十进制的科学技术法来存储数字, 那么我们只需要保存 有效数字 和 指数 这两个数据就能表示一个数字了.
JS 内存储数据与上面类似, 只不过存储用的是二进制, 不是十进制, 即有效数字都是 0 或者 1
为什么会有精度丢失的问题呢?
我们简单地还原数据精度丢失的整个过程, 大家就明白了. 为了方便理解, 我们作几个假设:
- 假设计算机用十进制存储数据, 然后每个 bit 能存 0~9 .
- 假设一种新的数据存储格式: 只使用 5 个 bits 存放有效数字, 指数则不限多少个 bits.
那么按照我们定义的格式, 123456 存储到计算机内是多少呢?
因为我们只有 5 个 bits 存放有效数字, 123456 的有效数字有 6 位, 所以肯定要舍去多余的 1 位, 为了尽可能保证数据精度, 我们只会丢失最后 1 位, 因为它最小.
所以按我们定义的格式和给定的空间, 123456 存储到计算机内就变成了: 1.2345 * 10^5. 之后我们再 取值时, 它就变成了 123450 了. 丢失了最后 1 位的数据 6.
看到这里应该就知道为什么会丢失精度了吧, 就是因为只要规定了用多少 bits 来存储有效数字, 那计算机内能存储的有效数字就是有限的, 必然会有精度丢失的情况发生.
2. 使用 JS 编程时什么时候发生精度丢失? 即 Number.MAX_SAFE_INTEGER 的值是多少?
回到 JS 的实现中, 底层使用二进制存储数据, 数据格式为: IEEE-754, 用 64 bits 的空间存储数据, 由于某些原因, 使用 52bits 的空间存储有效数字, 但是实际存储了 52 + 1 = 53bits 的有效数字信息(因为第 1 个有效数字始终是 1, 不需要存储), 11 bits 的指数位信息.
那么它们各自的取值范围是多少呢?
有效数字: [0, 2^53 - 1] 指数位: [-1022, 1023] , 指数位还要考虑负指数的情况, 所以使用的是补码形式存储的数据, 还有一些其他的原因. 导致最终的结果不是[0, 2047]
按照上面我们以自定义数据格式举的例子, 应该明白为什么会有精度丢失了, 那在 JS 里数字大于多少时会丢失呢, 也就是 Number.MAX_SAFE_INTEGER 是多少呢?
这个主要跟有效数字表示的范围有关系, 与指数位关系不大(也有关系,后面会提到).
因为指数负责控制小数点的移动. 还是举我们那个例子, 1.23456 * 10^5, 有效数字有 5bits, 只要指数能表示的数字大于5, 那么就肯定能准确表示 [0, 123456]的所有整数.
对应到 IEEE-754 使用64 bits 的方案中, 只要指数能够大于 52 即可.
所以Number.MAX_SAFE_INTEGER是多少, 就看 IEEE-754 使用 64 bits 的方案里, 有效数字最大是多少.
如果存储有效数字的 53bits 全为 1, 那应该是能准确表示的最大数字了吧?
此时表示的数字是: 2^53 -1.
如果在控制台打印一下 Number.MAX_SAFE_INTEGER, 就会发现这个数字就是 2^53 -1.
console.log(Number.MAX_SAFE_INTEGER === 2**53 - 1) // true
好像我们推测对了, 那到底对不对呢?
查阅一下规范中对Number.MAX_SAFE_INTEGER的定义:
The value of Number.MAX_SAFE_INTEGER is the largest integer n such that n and n + 1 are both exactly representable as a Number value.
翻译一下就是: 使得 n 和 n+1 都能被精确表示为 Number 类型的最大的那个数字.
有点绕口, 其实就是不断得增加 n 的值, 一直到 n+1能被精确表示(不会丢失精度), 但 n+2 开始丢失精度, 取这时的 n 为Number.MAX_SAFE_INTEGER.
再回看我们刚刚的推导, 将以下几个数字转为二进制
- 2^53 -1 : 11......111, 一共是 53bits: 全是 1
- 2^53 : 100......000, 一共是 54bits: 1 个 1, 53 个 0
- 2^53 + 1: 100......001, 一共是 54bits: 1 个 1, 52 个 0, 最后再接 1 个 1
我们前面提到JS 底层实现只能存储下 53bits 的有效数字, 所以:
- 对于 2^53 -1: 我们能完整存下它的 53 个 1 , 所以对于 [0, 2^53 - 1]的数字都可以完整存下有效数字, 不会出现精度丢失.
- 对于 2^53: 我们只能存下它的前 53 位, 最后 1 位的那个 0 被舍去了, 但是因为最后 1 位是 0, 所以舍去并不会导致其精度丢失
- 对于 2^53 + 1: 我们只能存下它的前 53 位, 最后 1 位的那个 1 被舍去了, 导致精度丢失.
结合上面规范里的定义, 我们终于找到了符合 Number.MAX_SAFE_INTEGER 定义的那个数字n: 2^ 53 - 1, 而不是 2^53.
参考资料
- JavaScript 浮点数陷阱及解法
- WikiPedia-Floating-point arithmetic
- WikiPedia-IEEE_754
- ECMAScript® 2021 Language Specification#sec-number.max_safe_integer
@buyijiuyang
因为 64.68 存储在 JavaScript 内存中的二进制是 1000000.10101110000101000111101011100001010001111011，实际上 64.68 小数部分的二进制真实的是 10101110000101000111 (无限重复)，受存储空间限制，存储策略使最后四位从原本的 1010 变为 1011，所以存储在 JavaScript 中的数比数学意义上的 64.68 会大，不仅是乘法，在四则运算中，浮点数转换成二进制后存在无限循环小数，都会有精度异常的情况。
解法：使用专业的四舍五入函数 Math.round() 来处理。但 Math.round(1.005 * 100) / 100 还是不行，因为 1.005 * 100 = 100.49999999999999。还需要把乘法和除法精度误差都解决后再使用 Math.round。可以使用后面介绍的 number-precision#round 方法来解决。 解决方案 回到最关心的问题：如何解决浮点误差。首先，理论上用有限的空间来存储无限的小数是不可能保证精确的，但我们可以处理一下得到我们期望的结果。 数据展示类 当你拿到 1.4000000000000001 这样的数据要展示时，建议使用 toPrecision 凑整并 parseFloat 转成数字后再显示，如下： parseFloat(1.4000000000000001.toPrecision(12)) === 1.4 // True 封装成方法就是： function strip(num, precision = 12) { return +parseFloat(num.toPrecision(precision)); } 为什么选择 12 做为默认精度？这是一个经验的选择，一般选12就能解决掉大部分0001和0009问题，而且大部分情况下也够用了，如果你需要更精确可以调高。
strip 是有效数字位吧……跟精度好像没占边
解法：使用专业的四舍五入函数 Math.round() 来处理。但 Math.round(1.005 * 100) / 100 还是不行，因为 1.005 * 100 = 100.49999999999999。还需要把乘法和除法精度误差都解决后再使用 Math.round。可以使用后面介绍的 number-precision#round 方法来解决。 解决方案 回到最关心的问题：如何解决浮点误差。首先，理论上用有限的空间来存储无限的小数是不可能保证精确的，但我们可以处理一下得到我们期望的结果。 数据展示类 当你拿到 1.4000000000000001 这样的数据要展示时，建议使用 toPrecision 凑整并 parseFloat 转成数字后再显示，如下： parseFloat(1.4000000000000001.toPrecision(12)) === 1.4 // True 封装成方法就是： function strip(num, precision = 12) { return +parseFloat(num.toPrecision(precision)); } 为什么选择 12 做为默认精度？这是一个经验的选择，一般选12就能解决掉大部分0001和0009问题，而且大部分情况下也够用了，如果你需要更精确可以调高。
strip 是有效数字位吧……跟精度好像没占边
另外，现在的 Math.round(1.005 * 100) / 100 === 1.005，虽然 Math.round(1.005 * 100) == 100.499999999
@mmmmmaster 我来回答一下这两个问题吧 😋 ① 十进制的 0.1 转换成二进制后，结果的确是 0.0001100110011001100（无限循环），这个二进制再进行 64 位浮点数存储得到：
0011111110111001100110011001100110011001100110011001100110011010，然后再将这个64位二进制转换回十进制的时候，得到的就是：0.100000000000000005551115123126。这个转换可以通过在线网站：http://www.binaryconvert.com/convert_double.html 进行②首先我们要知道
[-2^53, +2^53]这个范围是称为 safe integers，超出这个范围的数字，就是 unsafe integers。对于对于 (2^53, 2^63) 之间的数会出现什么情况呢？(2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数 (2^54, 2^55) 之间的数会四个选一个，只能精确表示4个倍数 ... 依次跳过更多2的倍数
所以我们看到 (2^53, 2^54) 范围的数字，都是间隔 2 的。
然后我们还要了解到不是 safe integers 的数字，计算结果不能确保其正确性。所以你提到的那几个计算中有些正确，有些不正确。
第二个问题关键在于不要混淆这两个概念即可。
最后，@camsong 这么理解对吧 😂
2 ** 53应该是开区间吧，不包括 2 ** 53，应该是(-2 ** 53, 2 ** 53), 尾数表精度，这也是JS里面最大安全整数
👇最大安全整数，IEEE 754标准一共有53位的尾数（包含省略的1位），类似于科学计数法，尾数表示的是精度，一个数对应一个IEEE 754的双精度浮点数，所以是安全的，当多个数对应一个浮点数的时候就是不安全的
Math.pow(2, 53) - 1 === Number.MAX_SAFE_INTEGER
👇最大数，根据IEEE 754标准的定义来的。为什么指数减去52，因为尾数表示的是1.1111（52位），尾数左移指数减去对应的位数，所以这个就是最大值
1 * Math.pow(2, 1023 - 52) * (Math.pow(2, 53) - 1) === Number.MAX_VALUE
由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1
为什么 E 最大值是 1023？E 的取值是 [0,2047]，然后减去中间数 1023， 那最大值不是 1024 吗
由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1
为什么 E 最大值是 1023？E 的取值是 [0,2047]，然后减去中间数 1023， 那最大值不是 1024 吗
The exponent field is an 11-bit unsigned integer from 0 to 2047, in biased form: an exponent value of 1023 represents the actual zero. Exponents range from −1022 to +1023 because exponents of −1023 (all 0s) and +1024 (all 1s) are reserved for special numbers.
2047被作为特殊类型处理， 即NaN, Infinity, -Infinity
由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1 最大的整数为什么是2^1024 - 1？最大数不是才到2^1023 * 2^-52*(2^53 - 1),也就是2^1024-2^971嘛？2^1024 - 1怎么比能表示的最大值还大呀, 这里不是很明白，希望能帮忙解答下。
最大可以表示的整数是 2^1024 - 1
由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1
为什么 E 最大值是 1023？E 的取值是 [0,2047]，然后减去中间数 1023， 那最大值不是 1024 吗
The exponent field is an 11-bit unsigned integer from 0 to 2047, in biased form: an exponent value of 1023 represents the actual zero. Exponents range from −1022 to +1023 because exponents of −1023 (all 0s) and +1024 (all 1s) are reserved for special numbers.
2047被作为特殊类型处理， 即NaN, Infinity, -Infinity
这个2^1024 - 1是最大整数是怎么计算来的，理论上2^970 * (2^54 - 1) 就已经是Infinity了
有一个疑惑，尾数M会先省略掉前面的1才存储到52位里面。那么1和0在存储的时候是怎么区分开来的呢？ 1 存储时 S = 0, E = 11个0, M = 52个0 （科学计数法前面的1省去） 0 存储时 S = 0，E = 11个0，M = 52个0吗？（0的科学计数法0.0 * 2^0 ? ） 这么按存储来开，没有办法区分0和1呀
为什么会有精度丢失? 什么时候发生精度丢失?
本次讨论主要解决两个问题:
- 使用 JS 编程时为什么会出现精度丢失?
- 使用 JS 编程时什么时候发生精度丢失? 即
Number.MAX_SAFE_INTEGER的值是多少?1. 使用 JS 编程时为什么会出现精度丢失?
建议先看下本 issue 里作者对于 JS 里怎么存储数字的介绍, 这里简述一下其原理, 只是为了便于解释精度丢失的议题:
JS 里用 64 bits 的空间存储数字, 使用 IEEE-754格式存储和解析数字, 用的是类似科学技术法的方式表示的数字. 比如: 123456 = 1.23456 * 10^5, 这里的 1.23456 就是有效数字, 10^5 的 5是指数. 可以看出来: 如果我们实现定义好使用十进制的科学技术法来存储数字, 那么我们只需要保存 有效数字 和 指数 这两个数据就能表示一个数字了.
JS 内存储数据与上面类似, 只不过存储用的是二进制, 不是十进制, 即有效数字都是 0 或者 1
为什么会有精度丢失的问题呢?
我们简单地还原数据精度丢失的整个过程, 大家就明白了. 为了方便理解, 我们作几个假设:
- 假设计算机用十进制存储数据, 然后每个 bit 能存 0~9 .
- 假设一种新的数据存储格式: 只使用 5 个 bits 存放有效数字, 指数则不限多少个 bits.
那么按照我们定义的格式, 123456 存储到计算机内是多少呢?
因为我们只有 5 个 bits 存放有效数字, 123456 的有效数字有 6 位, 所以肯定要舍去多余的 1 位, 为了尽可能保证数据精度, 我们只会丢失最后 1 位, 因为它最小.
所以按我们定义的格式和给定的空间, 123456 存储到计算机内就变成了: 1.2345 * 10^5. 之后我们再 取值时, 它就变成了 123450 了. 丢失了最后 1 位的数据 6.
看到这里应该就知道为什么会丢失精度了吧, 就是因为只要规定了用多少 bits 来存储有效数字, 那计算机内能存储的有效数字就是有限的, 必然会有精度丢失的情况发生.
2. 使用 JS 编程时什么时候发生精度丢失? 即
Number.MAX_SAFE_INTEGER的值是多少?回到 JS 的实现中, 底层使用二进制存储数据, 数据格式为:
IEEE-754, 用64 bits的空间存储数据, 由于某些原因, 使用52bits的空间存储有效数字, 但是实际存储了52 + 1 = 53bits的有效数字信息(因为第 1 个有效数字始终是 1, 不需要存储), 11 bits 的指数位信息.那么它们各自的取值范围是多少呢?
有效数字: [0, 2^53 - 1] 指数位: [-1022, 1023] , 指数位还要考虑负指数的情况, 所以使用的是补码形式存储的数据, 还有一些其他的原因. 导致最终的结果不是[0, 2047]
按照上面我们以自定义数据格式举的例子, 应该明白为什么会有精度丢失了, 那在 JS 里数字大于多少时会丢失呢, 也就是
Number.MAX_SAFE_INTEGER是多少呢?这个主要跟有效数字表示的范围有关系, 与指数位关系不大(也有关系,后面会提到). 因为指数负责控制小数点的移动. 还是举我们那个例子, 1.23456 * 10^5, 有效数字有 5bits, 只要指数能表示的数字大于5, 那么就肯定能准确表示 [0, 123456]的所有整数. 对应到
IEEE-754使用64 bits的方案中, 只要指数能够大于 52 即可.所以
Number.MAX_SAFE_INTEGER是多少, 就看IEEE-754使用64 bits的方案里, 有效数字最大是多少. 如果存储有效数字的 53bits 全为 1, 那应该是能准确表示的最大数字了吧? 此时表示的数字是: 2^53 -1. 如果在控制台打印一下Number.MAX_SAFE_INTEGER, 就会发现这个数字就是 2^53 -1.console.log(Number.MAX_SAFE_INTEGER === 2**53 - 1) // true好像我们推测对了, 那到底对不对呢?
查阅一下规范中对
Number.MAX_SAFE_INTEGER的定义:The value of Number.MAX_SAFE_INTEGER is the largest integer n such that n and n + 1 are both exactly representable as a Number value.
翻译一下就是: 使得 n 和 n+1 都能被精确表示为
Number类型的最大的那个数字. 有点绕口, 其实就是不断得增加 n 的值, 一直到 n+1能被精确表示(不会丢失精度), 但 n+2 开始丢失精度, 取这时的 n 为Number.MAX_SAFE_INTEGER.再回看我们刚刚的推导, 将以下几个数字转为二进制
- 2^53 -1 : 11......111, 一共是 53bits: 全是 1
- 2^53 : 100......000, 一共是 54bits: 1 个 1, 53 个 0
- 2^53 + 1: 100......001, 一共是 54bits: 1 个 1, 52 个 0, 最后再接 1 个 1
我们前面提到JS 底层实现只能存储下 53bits 的有效数字, 所以:
- 对于 2^53 -1: 我们能完整存下它的 53 个 1 , 所以对于 [0, 2^53 - 1]的数字都可以完整存下有效数字, 不会出现精度丢失.
- 对于 2^53: 我们只能存下它的前 53 位, 最后 1 位的那个 0 被舍去了, 但是因为最后 1 位是 0, 所以舍去并不会导致其精度丢失
- 对于 2^53 + 1: 我们只能存下它的前 53 位, 最后 1 位的那个 1 被舍去了, 导致精度丢失.
结合上面规范里的定义, 我们终于找到了符合
Number.MAX_SAFE_INTEGER定义的那个数字n: 2^ 53 - 1, 而不是 2^53.参考资料
这样为什么一开始设计的时候不把尾数位划大一点，指数位划小几位呢？
